
第6章 :储能元件 重点: 1.电容、电感元件的VCR关系 2.电容电感的串并联
1. 电容、电感元件的VCR关系 ⚫ 重点: 第6章 储能元件 2. 电容电感的串并联
6.1电容元件(capacitor)) 电容器 在外电源作用下 两极板上分别带上等量异号电荷,撒去电 源,板上电荷仍可长久地集聚下去,是一 种储存电能的部件。 1.定义 电容元件 储存电能的元件。其 特性可用u~q平面 上的一条曲线来描述 f(u,9)=0 库伏 特性
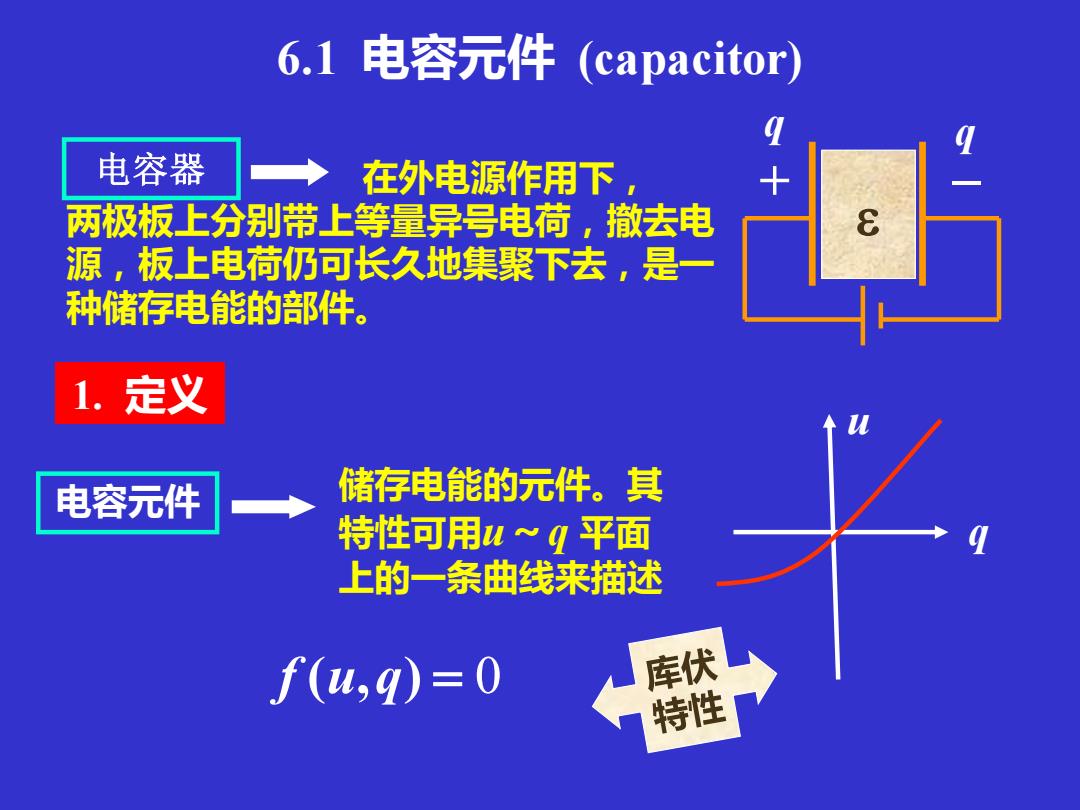
6.1 电容元件 (capacitor) 电容器 _ q + q 在外电源作用下, 两极板上分别带上等量异号电荷,撤去电 源,板上电荷仍可长久地集聚下去,是一 种储存电能的部件。 1. 定义 电容元件 储存电能的元件。其 特性可用u~q 平面 上的一条曲线来描述 f (u,q) = 0 q u

2.线性定常电容元件 任何时刻,电容元件极板上的电荷与电压u成正比。q~W 特性是过原点的直线 4=Cu or C=1 oc tan a W ● 电路符号 大0 -9 单位 C称为电容器的电容,单位:F(法 Farad,法拉),常用uF,pF等表示
任何时刻,电容元件极板上的电荷q与电压 u 成正比。q ~ u 特性是过原点的直线 ⚫ 电路符号 2. 线性定常电容元件 C + - u +q -q = = tan u q q Cu or C C 称为电容器的电容, 单位:F (法) (Farad,法拉), 常用F,p F等表示。 q O u ⚫ 单位
线性电容的电压、电流关系 电容元件VCR 的微分关系 dq du dt dt u、i取关 联参考方向 表明: (1)i的大小取决于u的变化率,与u的大小无关 电容是动态元件; (2)当4为常数(直流)时,i=0。电容相当于开路,电容 有隔断直流作用: (3)实际电路中通过电容的电流为有限值,则电容电压 必定是时间的连续函数
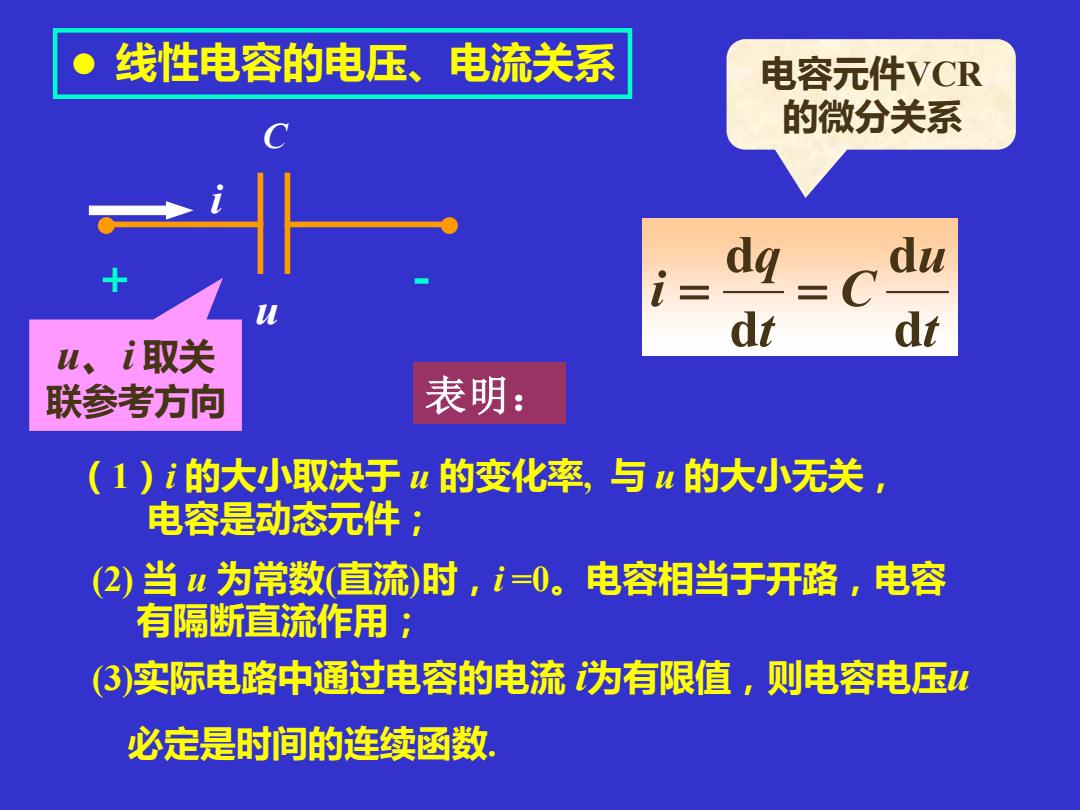
t u C t q i d d d d = = ⚫ 线性电容的电压、电流关系 C + - u i u、i 取关 联参考方向 电容元件VCR 的微分关系 表明: (1)i 的大小取决于 u 的变化率, 与 u 的大小无关, 电容是动态元件; (2) 当 u 为常数(直流)时,i =0。电容相当于开路,电容 有隔断直流作用; (3)实际电路中通过电容的电流 i为有限值,则电容电压u 必定是时间的连续函数

电容元件VCR的积分关系 dq =C du dt dt )=cfds-cide+chids =+己Jid6 表明 电容无件有记忆电流的作用,故称电容为记忆元件 注 dq du 1 dt (1)当,为非关联方向时,上述微分和积分表达 式前要冠以负号; (2)上式中u()称为电容电压的初始值,它反映电 容初始时刻的储能状况,也称为初始状态
电容元件有记忆电流的作用,故称电容为记忆元件 (1)当 u,i为非关联方向时,上述微分和积分表达 式前要冠以负号; ( ) d ( ) d d = + = + = − − t t t t t t i ξ C u idξ C i ξ C i ξ C u t t 0 0 0 0 1 1 1 1 表明 注 t u C t q i d d d d = = 电容元件VCR的积分关系 C + - u i (2)上式中u(t0 )称为电容电压的初始值,它反映电 容初始时刻的储能状况,也称为初始状态。 t u C t q i d d d d = − = −

u、i取关 3.电容的功率和储能 联参考方向 du 功率 卫=ui=u.C dt (1)当电容充电,q个,du/d>0,则>0,电容吸 收功率。 (2)当电容放电,q↓,d/d0,则i<0,电容发 出功率. 表明 电容能在一段时间内吸收外部供给的能量转化为电场能 量储存起来,在另一段时间内又把能量释放回电路,因此电 容元件是无源元件、是储能元件,它本身不消耗能量
3. 电容的功率和储能 t u p ui u C d d = = (1)当电容充电, q , d u/d t>0,则i>0,电容吸 收功率。 (2)当电容放电, q , d u/d t<0,则i<0,电容发 出功率. ⚫ 功率 表明 电容能在一段时间内吸收外部供给的能量转化为电场能 量储存起来,在另一段时间内又把能量释放回电路,因此电 容元件是无源元件、是储能元件,它本身不消耗能量。 u、 i 取关 联参考方向 C + - u +q -q C + - u +q -q i

电容的储能 -oFec-o- C(- 2 从t到t电容储能的变化量: 2G0-G)-200-c 表明 (1)电容的储能只与当时的电压值有关,电容 电压不能跃变,反映了储能不能跃变; (2)电容储存的能量一定大于或等于零
(1)电容的储能只与当时的电压值有关,电容 电压不能跃变,反映了储能不能跃变; (2)电容储存的能量一定大于或等于零。 从t0到 t 电容储能的变化量: ( ) 2 1 ( ) 2 1 ( ) 2 1 ( ) 2 1 0 2 2 0 2 2 q t C q t C W Cu t Cu t C = − = − 0 2 1 2 1 2 1 2 1 ξ 2 1 2 2 0 2 2 2 = = = = = − − − = − − ( ) ( ) d ( ) ( ) ( ) d d ( ) q t C Cu t ξ Cu Cu t Cu ξ u W Cu u t t C 若 ⚫ 电容的储能 表 明

例求电流、 电容的功率P()和储能W() 解 us(t)的函数表示式为: C 0.5F t≤0 2t 0≤t≤1s w,(t)= -2t+4 电源波形 1≤t≤2s t≥2s 解得电流 边A 2 tls t<0 dus 1 0≤t<1s i(t)C dt -1 1≤t<2s 0 t≥2s
例 + - u (t) s C 0.5F 求电流i、电容的功率P (t)和储能W (t) i 1 2 t /s 2 0 u/V 电源波形 解 uS (t)的函数表示式为: − + = t s t t s t t s t u t s 0 2 2 4 1 2 2 0 1 0 0 ( ) − = = t s t s t s t dt du i t C s 0 2 1 1 2 1 0 1 0 0 ( ) 解得电流 2 1 t /s 1 i/A -1
p(t)u(t)i(t) p/ 吸收功率 0 2 t≤0 2t 0≤t≤1s 2t-4 1≤t≤2s t/s 0 t≥2s 2 释放功率 W0-cr- 0 t≤0 0≤t≤1s (t-2)2 1≤t≤2s 1 0 t≥2s
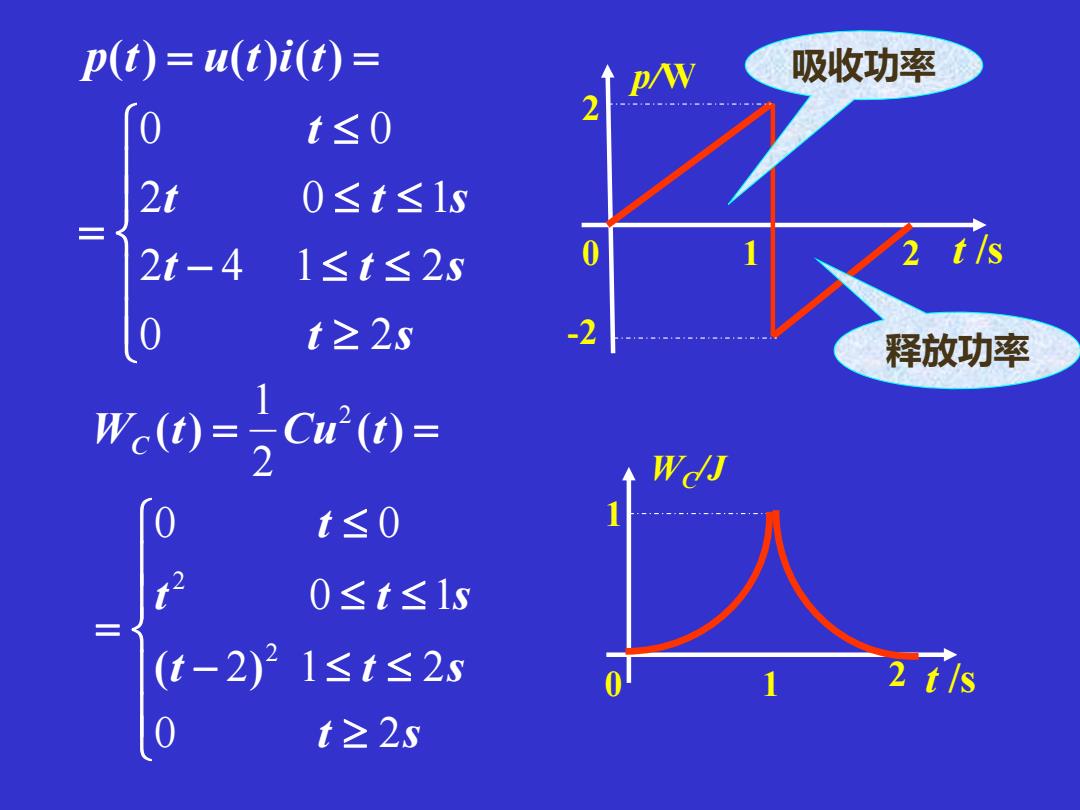
− = = = t s t t s t t s t p t u t i t 0 2 2 4 1 2 2 0 1 0 0 ( ) ( ) ( ) 1 2 t /s 2 0 p/W -2 − = = = t s t t s t t s t W t Cu t C 0 2 2 1 2 0 1 0 0 2 1 2 2 2 ( ) ( ) ( ) 2 1 t /s 1 0 WC/J 吸收功率 释放功率