4.2替代定理(Substitution Theorem 1.替代定理 对于给定的任意一个电路, 若某一支路电压为山、 电流为k,那么这条支路就可以用一个电压等于的 独立电压源,或者用一个电流等于的独立电流源 或用一R=W的电阻来替代,替代后电路中全部电压 和电流均保持原有值(解答唯一)。 R=uKik k
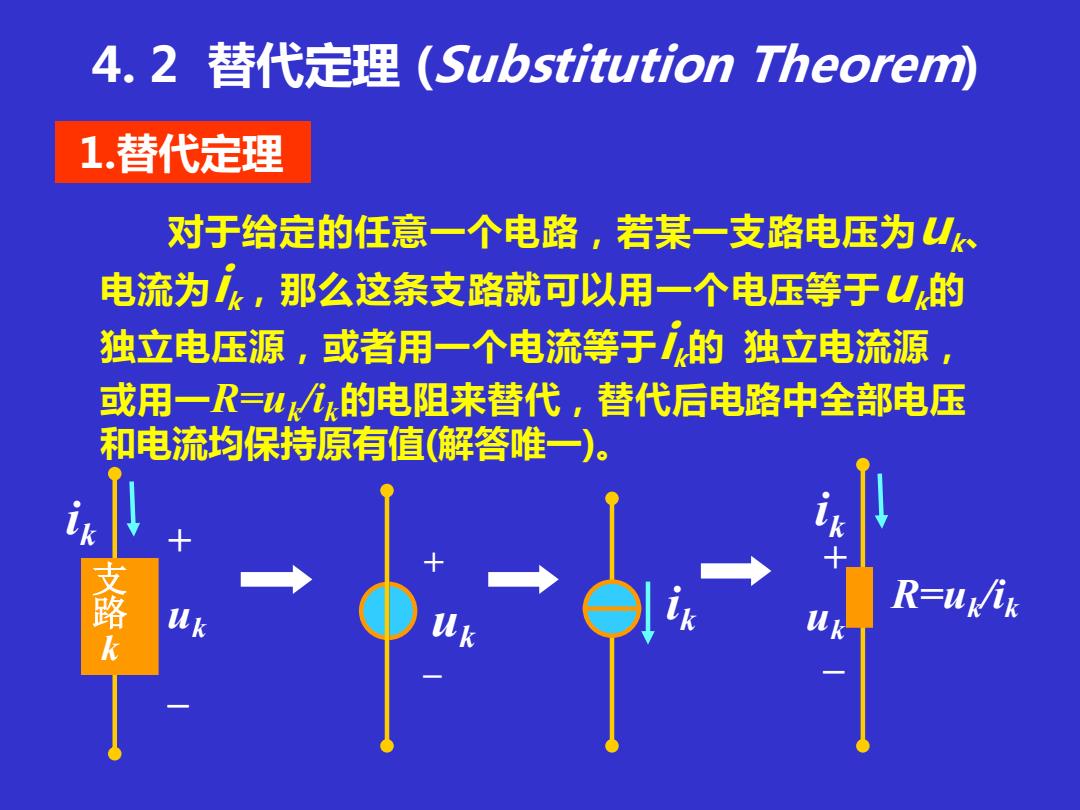
4. 2 替代定理 (Substitution Theorem) 对于给定的任意一个电路,若某一支路电压为uk、 电流为ik,那么这条支路就可以用一个电压等于uk的 独立电压源,或者用一个电流等于ik的 独立电流源, 或用一R=uk /ik的电阻来替代,替代后电路中全部电压 和电流均保持原有值(解答唯一)。 ik 1.替代定理 支 路 k ik + – uk + – uk ik + – uk R=uk /ik
2.定理的说明 A A Wk Wk k A Wk 证毕! Mk
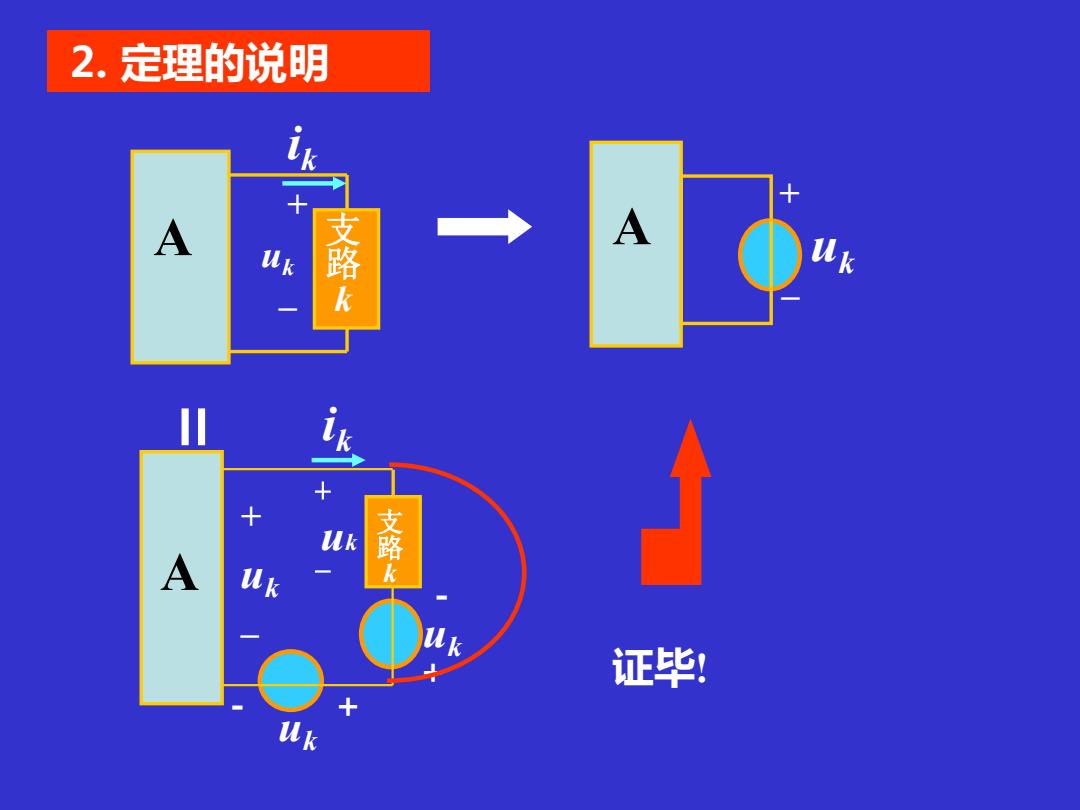
A ik+–uk 支路k A +– u k u k u k u k - + + A - ik +–u k 支路k 证毕 ! 2. 定理的说明 =

原因替代前后KCL,KVL关系相同 , 其余支路的、关系 不变。用W替代后,其余支路电压不变(KVL),其余支路 电流也不变,故第k绦支路也不变(KC)。用替代后, 其余支路电流不变KCL),其余支路电压不变,故第条支 路u也不变KVL)。 支路电流法方程: ++=0 k kCL方 +弘+…=0 A 使用4替代
替代前后KCL,KVL关系相同,其余支路的u、i关系 不变。用uk替代后,其余支路电压不变(KVL),其余支路 电流也不变,故第k条支路ik也不变(KCL)。用ik替代后, 其余支路电流不变(KCL),其余支路电压不变,故第k条支 路uk也不变(KVL)。 原因 支路电流法方程: + + = + + = ...... ... ... ... 0 ....... ... ... 0 k k u KVL i KCL 方程 方程使用uk替代 A ik + – uk 支 路 k R A + – uk ik ’
原方程 使用4替代后: KCL方程 +i+.=0 KCL方 .+1+.=▣0 KVZ方程 +w+0 K方程 .+弘+…=0 年用年8 方程组的其他约束关系相同 A A 替代前后具有相同的解
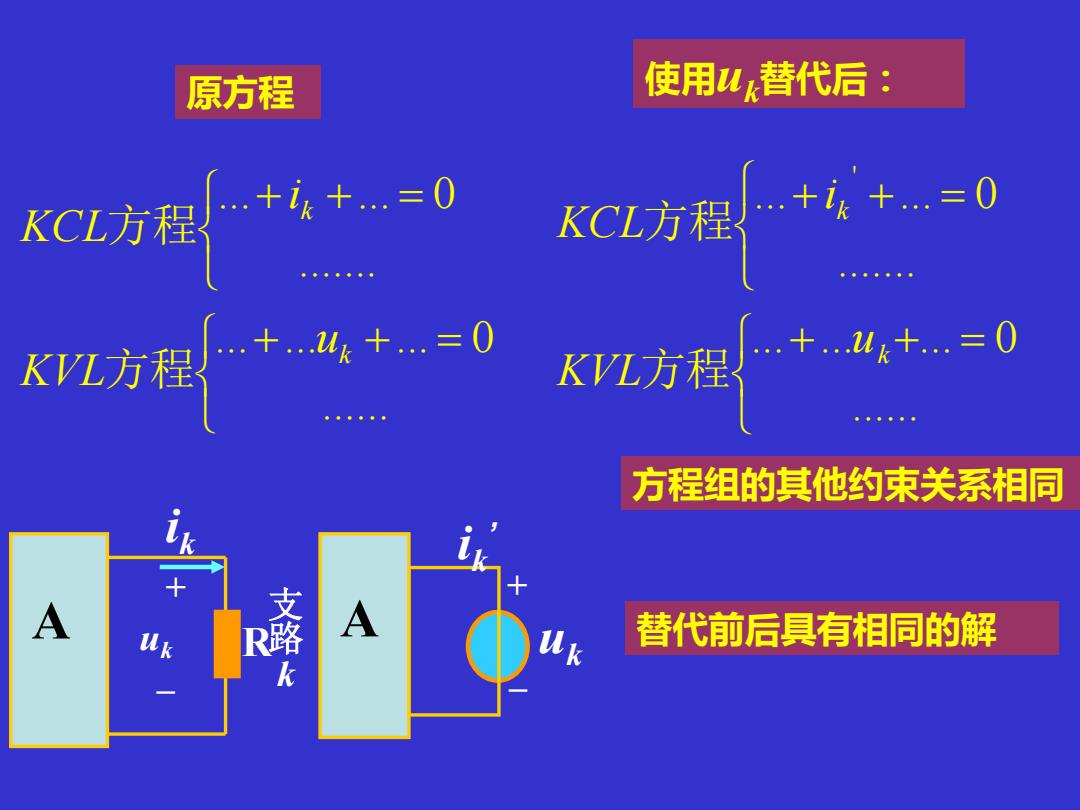
+ + = + + = ...... ... ... ... 0 ....... ... ... 0 ' k k u KVL i KCL 方程 方程 + + = + + = ...... ... ... ... 0 ....... ... ... 0 k k u KVL i KCL 方程 方程 原方程 使用uk替代后: 方程组的其他约束关系相同 A 替代前后具有相同的解 ik + – uk 支 路 k R A + – uk ik ’
2A 5A 2.5A 7A U=? 10V 注: 1.替代定理既适用于线性电路 ,也适用于非线性电路。 无电压源回路; 2.替代后电路必须有唯一解 无电流源节点。 3.替代后其余支路及参数不能改变
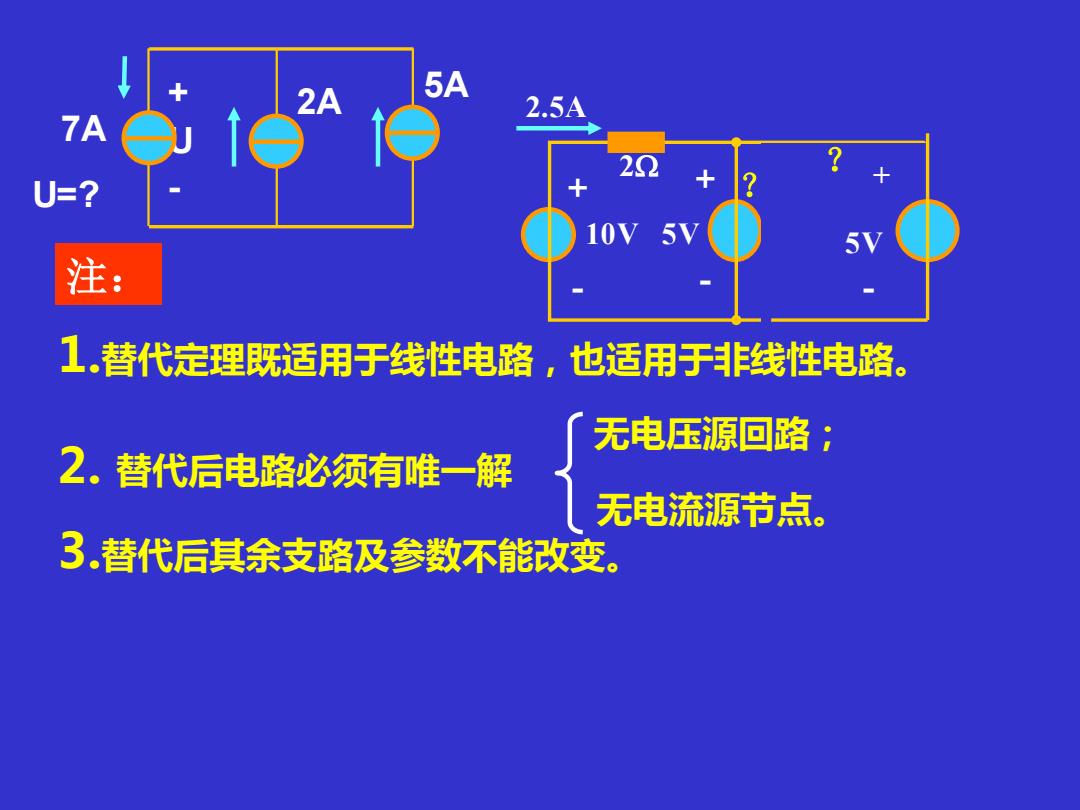
注: 1.替代定理既适用于线性电路,也适用于非线性电路。 3.替代后其余支路及参数不能改变。 2. 替代后电路必须有唯一解 无电压源回路; 无电流源节点。 1.5A 10V 5V 2 5 + - - + 2.5A 1A 5V + - ? ? 7A 2A + 5A - 1 U U=7V? 7A
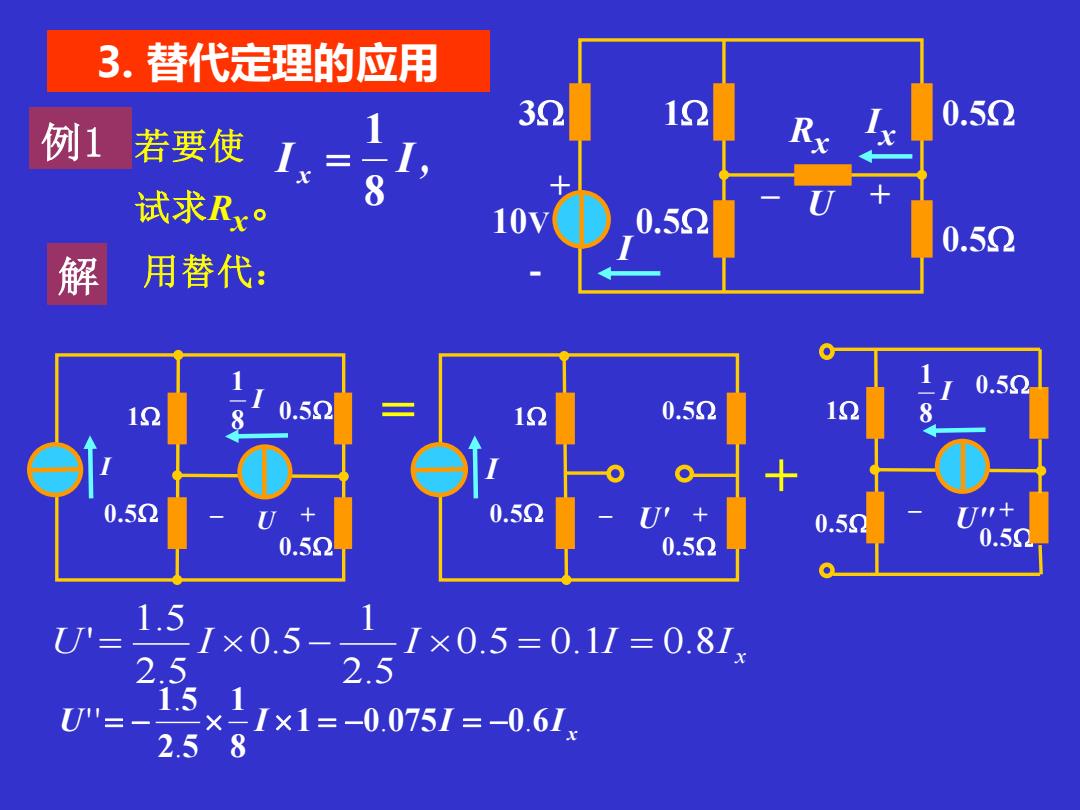
3.替代定理的应用 3 12 0.52 例1若要使 1=。1, 试求Rxo 8 0.52 0.52 解 用替代: 0.5Ω 8 0.50 1 0.50 12 8 + 0.52 0.52 0.5q 1+ 0.52 0.52 0.5Q U'= 151×0.5-1 1×0.5=0.11=0.81 21 2.5 =I×1=-0.0751=-0.6Ix 2.5 8
例1 若要使 试求Rx。 I I, x 8 1 = 3. 替代定理的应用 0.5 0.5 + 10V 3 1 Rx Ix – U + I 0.5 解 用替代: - = + 0.5 1 0.5 – U + I 0.5 I 8 1 0.5 1 0.5 – U' + I 0.5 0.5 0.5 1 – U'' + 0.5 I 8 1 x U I I 0.5 0.1I 0.8I 2.5 1 0.5 2.5 1.5 ' = − = = x U I 1 0 075I 0 6I 8 1 2 5 1 5 . . . . '' = − = − = −
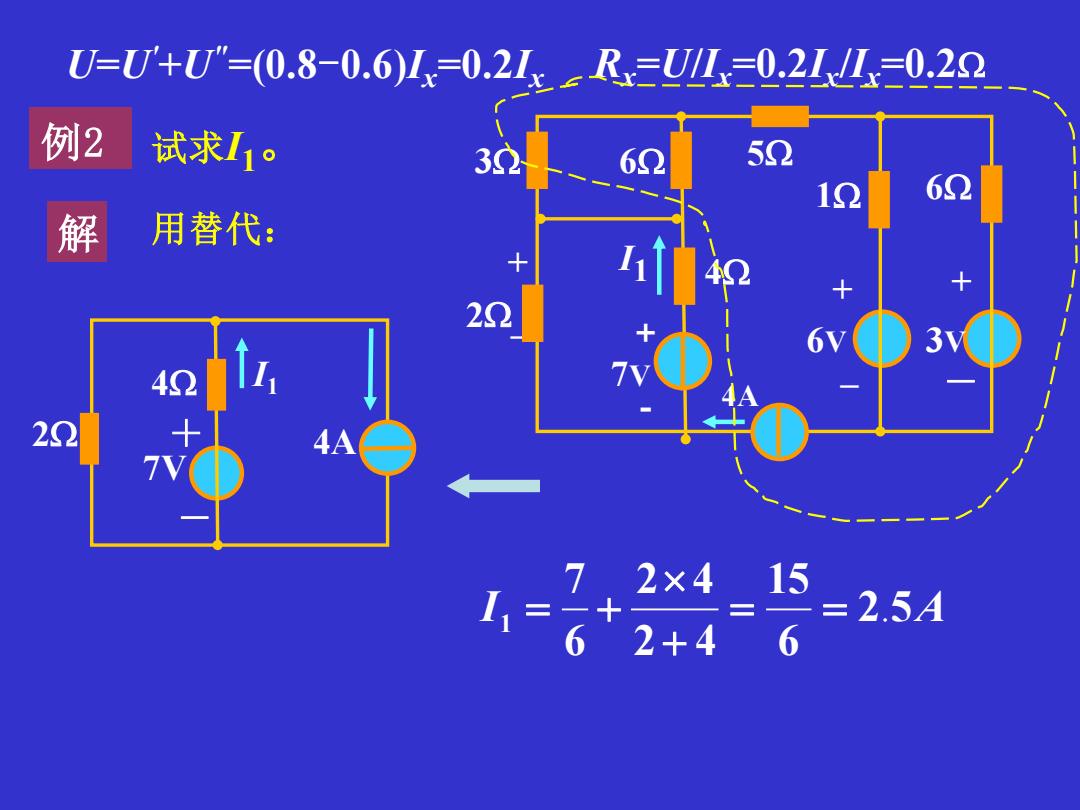
U=U'+U"=(0.8-0.6)1x=0.21xR==0.2=022 例2 试求I1。 32 62 52 60 解 用替代: 22 42 22 72×4 15 1121 =2.5A 62+4 6
U=U'+U"=(0.8-0.6)Ix=0.2Ix Rx =U/Ix=0.2Ix /Ix=0.2 例2 试求I1。 解 用替代: 6 5 + – 7V 3 6 I1 – + 1 + - 2 + - 6V 3V 4A 4 2 4 + 4A - 7V I1 I 2 5A 6 15 2 4 2 4 6 7 1 = = . + = +
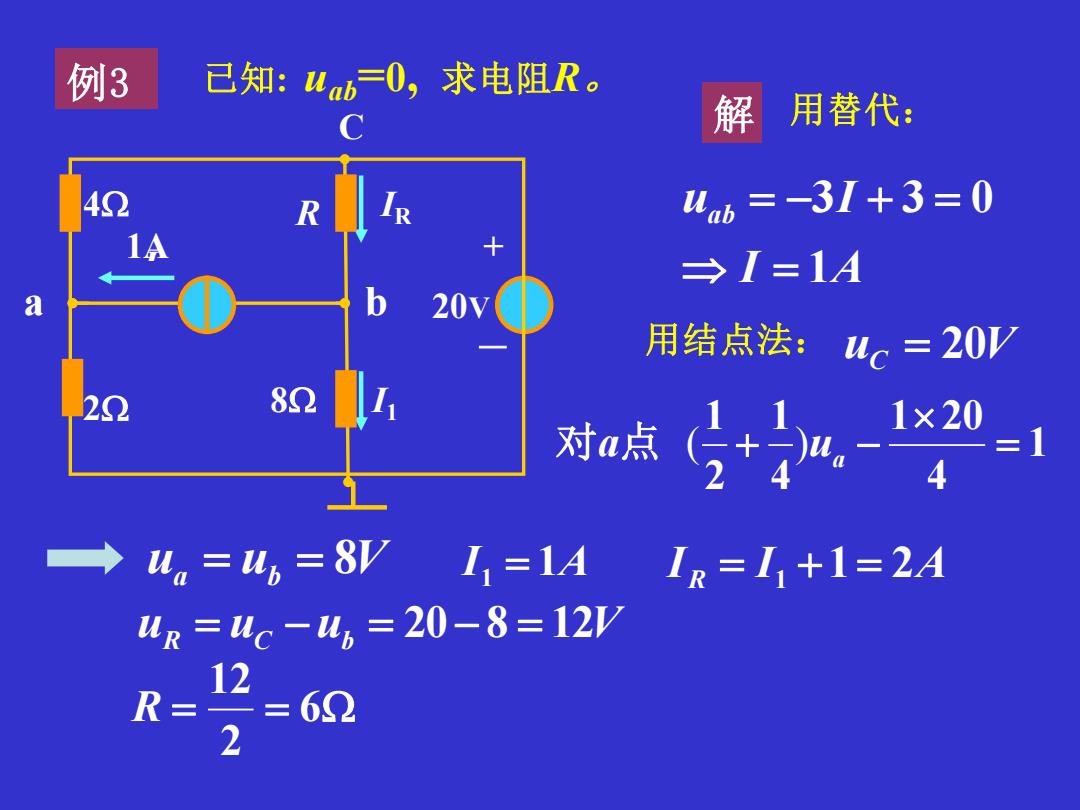
例3 已知:4ab=0,求电阻R。 解 用替代: 42 R 4ab=-31+3=0 1A →I=1A a 用结点法:4c=20V 22 82 对a点 1×20 =1 →4n=u2=8V I=1A IR=I1+1=2A Wr=4c-u,=20-8=12y R= 12 =62 2
I1 R IR 8 3V 4 b + - 2 + - a 20V 3 I 例3 已知: uab =0, 求电阻R。 C 1A 解 用替代: I A u I ab 1 3 3 0 = = − + = 用结点法: uC = 20V 1 4 1 20 4 1 2 1 = 对a点 ( + )ua − ua = ub = 8V I1 = 1A I R = I1 +1 = 2A uR = uC − ub = 20− 8 = 12V = = 6 2 12 R

例4 2V电压源用多大的电阻置换而不影响电路的工作状态。 42 10.5A 2 20 10 10 22 解 应求电流I,先化简电路。应用结点法得: 10.2 w1=6/1.2=5/ 2 2 11=(5-2)/2=1.5A I=1.5-0.5=1A R=2/1=2Q
例4 2V电压源用多大的电阻置换而不影响电路的工作状态。 4 4V 10 3A + - 2 + 2V - 10 2 解 I 0.5A I1 10V + - 2 + 2V - 5 2 1 应求电流I,先化简电路。 6 2 2 2 10 ) 5 1 2 1 2 1 ( + + u1 = + = u1 = 6/1.2 = 5V I1 = (5− 2)/ 2 = 1.5A I = 1.5− 0.5 = 1A R = 2/1 = 2 应用结点法得:
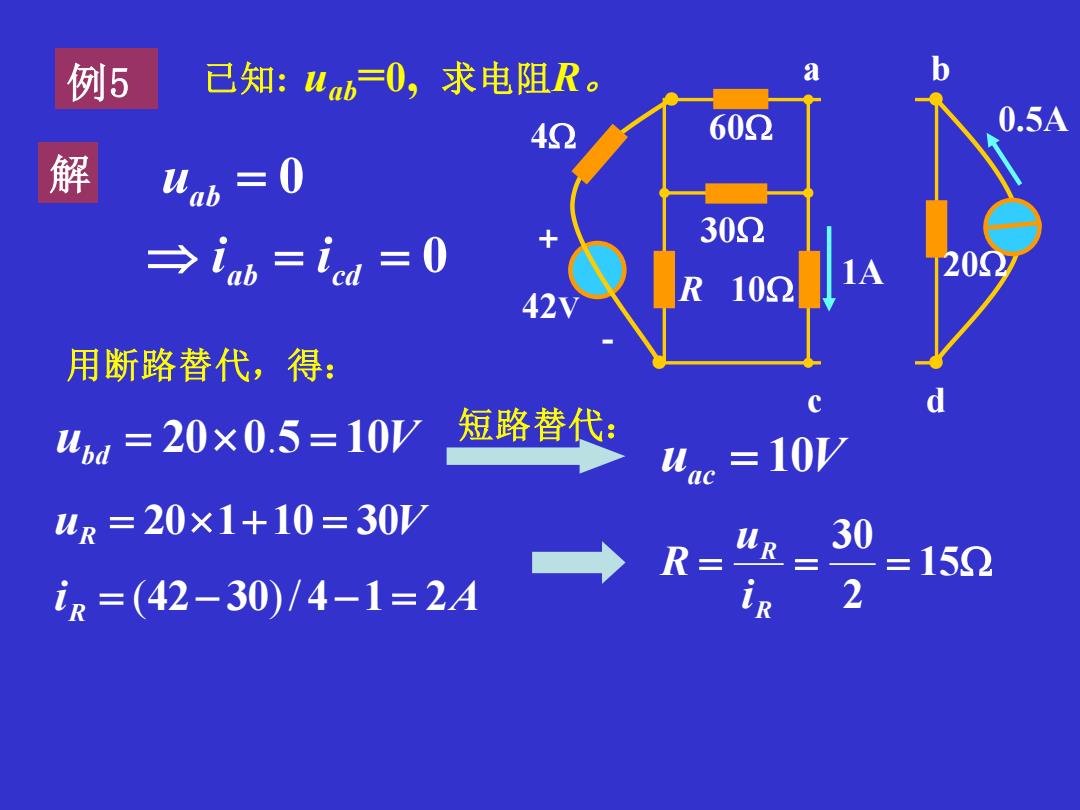
例5 已知:Wab=0,求电阻R。 b 42 602 0.5A 解 4ab=0 302 →iab=ica=0 20① 102 1A 用断路替代,得: d d=20x0.5=10V 短路替代: ac=10/ uR=20×1+10=30 4R= 30 R= =15Ω iR=(42-30)/4-1=2A 2
例5 已知: uab =0, 求电阻R。 解 0 0 = = = ab cd ab i i u 用断路替代,得: ubd = 200.5 = 10V 短路替代: uac = 10V 4 42V 30 0.5A + - 60 25 10 20 40 a b c d R uR = 201+10 = 30V 1A i R = (42− 30)/ 4−1 = 2A = = = 15 2 30 R R i u R