
试卷代号:2320 座位号■■ 中央广播电视大学2013一2014学年度第一学期“开放专科”期末考试 物流管理定量分析方法· 试题 2014年1月 题号 二 三 四 总 分 分数 导数基本公式: (1)(c)'=0(c为常数) (2)(x“)'=ax-1(a为常数) (3)(e*)'=e (4)(a2)'=alna(a>0,a≠1) 6)Inx)-子 (6)(1og.x)'=1a>0,a≠1) 积分的基本公式: (1)dz=x+c 2xrd。中+da≠-1) (3)∫edr=e+c 4ward=+ca>0a≠) (5)ds=Inlxc MATLAB的常用标准函数表 函数 功能 abs(x) 绝对值函数,即|x log(x) 以e=2.71828…为底的对数函数,即自然对数lnx 1og10(x) 以10为底的对数函数,即常用对数lgx xa a次方的幂函数,即x sqrt(x) x的开平方根函数,即√: a'x 以a为底的指数函数,即a” exp(x) 以e为底的指数函数,即e 1238
试卷代号 2 3 2 座位号 中央广播电视大学 4学年度第一学期"开放专科"期末考试 物流管理定量分析方法试题 2014 年1 |题号 - |分数 l I I.~J 导数基本公式 (1) (c)' =O(c (3) (eX)' =eX (5)(lnz)'=iZ 积分的基本公式 =ex+c (5) r1.dx = in I x J X MATLAB 标准 数表 (2) (x a ) ' =ax a - 1 (a 为常 (4) (aX)' =axina(α>O,a =l= 1) (6) 〈logaz)'=÷(a〉0 1) xina (2) Jα rxadx =~x + c(a =1=- 1) (的 +c(a > a,a =1= 1) J ina abs(x) 绝对值函数,即 log(x) 2 8 对数 n x log10(x) 对数 x-a sqrt(x) 开平 -IX ax exp(x) 1238

得分 评卷人 一、单项选择题(每小题4分,共20分) 1.若某物资的总供应量大于总需求量,则可增设一个(),其需求量取总供应量与总需 求量的差额,并取各产地到该销地的单位运价为0,可将不平衡运输问题化为平衡运输问题。 ·A.需求量 B.供应量 C.虚产地 D.虚销地 2.某物流公司有三种化学原料A1,A2,A3。每公斤原料A1含B1,B2,B3三种化学成分的 含量分别为0.7公斤、0.2公斤和0.1公斤:每公斤原料A2含B1,B2,B3的含量分别为0.1公 斤、0.3公斤和0.6公斤;每公斤原料A含B1,B2,B的含量分别为0.3公斤、0.4公斤和0.3 公斤。每公斤原料A1,A2,A的成本分别为500元、300元和400元。今需要B1成分至少100 公斤,B2成分至少50公斤,B,成分至少80公斤。为列出使成本最小的线性规划模型,设需要 原料A1,A2,A的数量分别为x1公斤、x2公斤和x3公斤,则化学成分B3应满足的约束条件 为()。 A.0.1x1+0.6x2十0.3x3≤80 B.0.1x1+0.6x2+0.3x3≥80 C.0.1x1+0.6x2+0.3x3=80 D.minS=500x1+300x2十400x3 12 3.设A= ,通过验证,可得A1=( 35 B. 3-5 2 D. 5-2 -31] 4.设某公司运输某物品的总成本(单位:百元)函数为C(q)=500+2g+q2,则运输量为 100单位时的边际成本为( )百元/单位。 A.202 B.702 C.10700 D.107 5.由曲线y=x3,直线x=1,x=2及x轴围成的曲边梯形的面积表示为()。 A.d B.z'dx D.-'dz 1239
|得分|评卷人| I I I 一、单项选择题{每小题 4分,共 0分} 1.若某物资的总供应量大于总需求量,则可增设一个( ) ,其需求量取总供应量与总需 求量的差额,并取各产地到该销地的单位运价为 0,可将不平衡运输问题化为平衡运输问题。 . A. 需求量B. c. 2. 物流 有三 学原料 l' 3 0 原料 化学成分 含量分别为 和O. 料A 为O. 斤、 3公斤和 6公斤 z每公斤原料 矶, 13 ;B 含量 、0.4 和0.3 公斤。每公斤原料 l,岛 成本 0元、 0元和 4 0 0元。今需要 成分 0 0 公斤 0公斤,且成分至少 0公斤。为列出使成本最小的线性规划模型,设需要 原料 l,儿 数量 l公斤、 z公斤和岛公斤,则化学成分 束 条件 )。 A. O. 1xl +0. 6xz 3X3~80 c. O. lxl +0. 6X2 +0. 3X3=80 B.0. xl 6X2 +0. 3X3 二 D. minS= 500Xl 十300X2 十400X3 A A AC37] c. [二 BClfJ D[J371 4. 某公 某物 品 的 成本 单位 =500 十2q 运输量 100 单位 )百元/单位。 A. 202 C.I0700 B. 702 D.I07 5. 积表 )。 A.I:巾 Z JU Z rllld12 c D. - I:巾 1239

得分 评卷人 二、计算题(每小题7分,共21分) 01-10 0 3 6.已知矩阵A=01-1,B= 1-12 ,求:BA 10 -2 7.设y=(1+x3)e,求:y 8.计算定积分:(3x2-e)dr 得 分 评卷人 三、编程题(每小题6分,共12分) 9.试写出用MATLAB软件计算函数y=elnx的二阶导数的命令语句。 10.试写出用MATLAB软件计算定积分∫匠的命令语句。 得 分 评卷人 四、应用题(第11、12题各14分,第13题19分,共47分) 11.某公司运输某种商品的固定成本为2万元,每多运输1吨商品,运输总成本增加1万 元,运输该商品g吨收取客户的收人(单位:万元)为R(g)=4g一0.5g。试求当运输量为多少 时,利润最大?最大利润为多少? 12.某物流公司下属企业欲制定生产A和B两种产品的生产计划。已知生产一件A产 品需要原材料1吨,动力1单位,生产设备3工时;生产一件B产品需要原材料2吨,动力1单 位,生产设备1工时。在一个生产周期内,可用原材料16吨,动力10单位,生产设备24工时。 每件A产品利润3千元,每件B产品利润4千元。试建立使企业能获得最大利润的线性规划 模型,并写出用MATLAB软件计算该线性规划问题的命令语句。 13.某公司从三个产地A1,A2,A,运送某物资到四个销地B1,B2,B,,B,各产地的供应量 (单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 1240
|得分|评卷人| I I I 二、计算题{每小题 7分,共 1分} 7. )e 算定积 :1 |得分|评卷人| I I I 三、编程题{每小题 6分,共 2分} 9. 用MATLAB 令语 r2 Jx 10. 用MATLAB 软件 定积 dx 令语 JI X 得分|评卷人 四、应用题{第 11、 2题备 4分,第 3题 9分,共 7分} 1. 输某 为2 万元 输1 成本 加1 元,运输该商品 q吨收取客户的收入(单位:万元)为 =句一 5q2 输量为 多 时,利润最大?最大利润为多少? 12. 物流 企业 产A 和B 两 种产 品 的 知 生 件A 品需要原材料 1吨,动力 1单位,生产设备 3工时;生产一件 B产品需要原材料 2吨,动力 1单 位,生产设备 1工时。在一个生产周期内,可用原材料 6吨,动力 0单位,生产设备 4工时。 每件 A产品利润 3千元,每件 B产品利润 4千元。试建立使企业能获得最大利润的线性规划 模型,并写出用 B软件计算该线性规划问题的命令语句。 13. 个产地AI' 运送某 地 鸟 产地 供应量 (单位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 1240
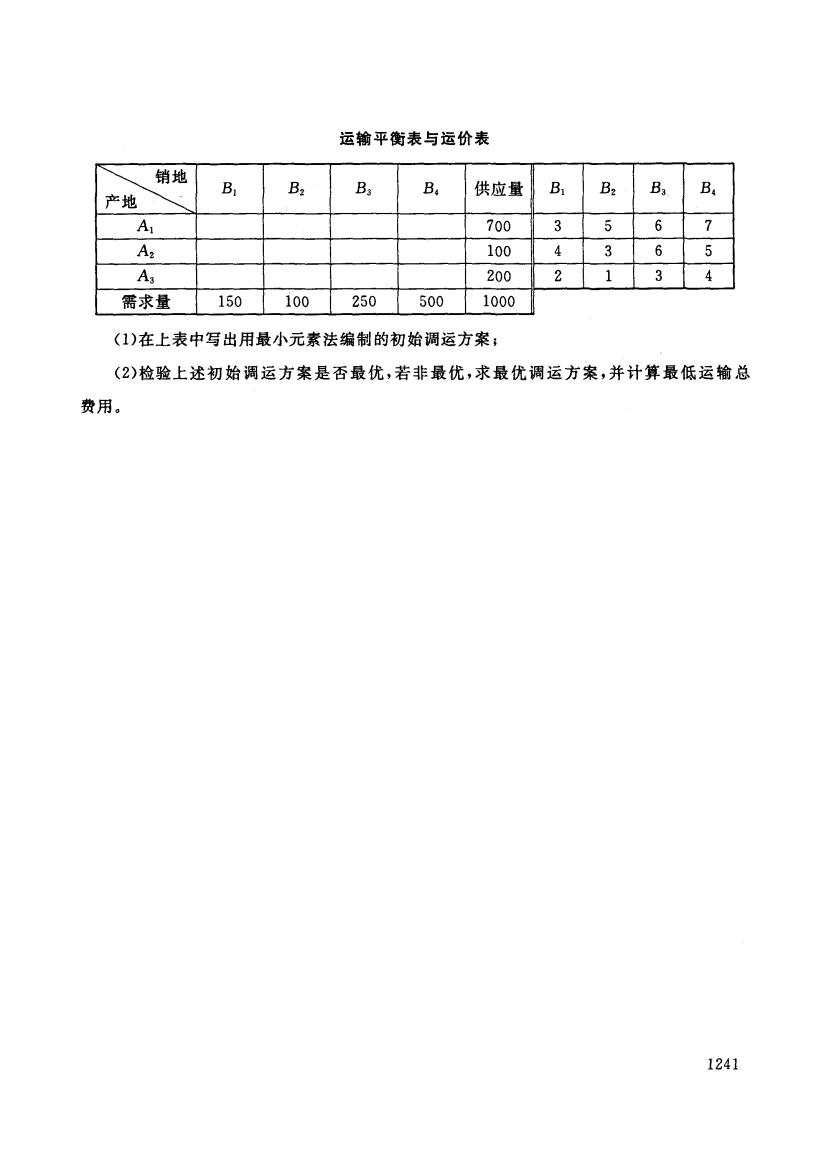
运输平衡表与运价表 销地 B B2 Ba B 供应量 B B2 Ba B 产地 A 700 3 5 6 7 A2 100 4 3 6 5 A 200 2 1 3 需求量 150 100 250 500 1000 (1)在上表中写出用最小元素法编制的初始调运方案; (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 1241
运输平衡表与运价表 泣可 BI B2 B3 B4 供应量 BI B2 B3 B4 AI 700 3 5 6 7 A2 100 4 3 6 5 A3 200 2 1 3 4 需求量 150 100 250 500 1000 (1)在上表中写出用最小元素法编制的初始调运方案 (2) 最 优 求 最 优 运 方 费用。 1241

试卷代号:2320 中央广播电视大学2013一2014学年度第一学期“开放专科”期末考试 物流管理定量分析方法试题答案及评分标准 (供参考) 2014年1月 一、单项选择题(每小题4分,共20分) 1.D 2.B 3.C 4.A 5.A 二、计算题(每小题7分,共21分) 1 -1 0 0 -1-67 6.BA= 0 1 -1 -1 2 3 2-3 7分 - 1 0 -2 7.y=(1+x3)'·e*+(1+x3)·(e)'=(3x2+1+x3e 7分 83x2-e)dz=(x3-e)8=2-e 7分 三、编程题(每小题6分,共12分) 9.>>clear >>syms x 2分 >>y=exp(x2)*log(x); 4分 >>diff(y,2) 6分 10.>>clear >syms x 2分 >>y=(sqrt(x)+1)/x2; 4分 >>int(y,1,2) 6分 四、应用题(第11、12题各14分,第13题19分,共47分】 11.运输q吨商品的成本函数为C(g)=q+2 3分 利润函数为L(g)=R(g)一C(g)=3q一0.5g2一2 8分 令ML(q)=3-q=0 1242
试卷代号 中央广播电视大学 4学年度第-学期"开放专科"期末考试 物流管理定量分析方法试题答案及评分标准 (供参考) 一、单项选择题{每小题 4分,共 0分} 1. D 2.B 3.C 二、计算题{每小题 7分,共 1分} 4.A mrlu -- -10o-- FO BA 7. y' = (l+x 3 )' • eX+ (l十 • (eX)' =(3x2+1 十x )e 8. f: 三、编程题{每小题 6分,共 2分} 9. »clear »syms x »y=exp(x·2) 赞log(x) ; »diff ,2) 10. »clear »syms x > >y= (sqrt(x)+D/x·2; »int(y,1,2) 四、应用题{第 11、 2题各 4分,第 3题 9分,共 7分} 1. 品 的 利润函数为 =3q一0.5q2_2 1242 2014 年1 5.A

得惟一驻点q=3吨。 12分 故当运输量为3吨时,利润最大。 13分 最大利润为L(3)=2.5万元。 14分 12.设生产A,B两种产品分别为x1件和x2件,显然,x1,x2≥0。 1分 maxS=3x+4x2 x1+2x2≤16 线性规划模型为: x1+x2≤10 8分 3x1十x2≤24 x1,x2≥0 计算该线性规划模型的MATLAB命令语句为: >>clear >>C=-[34]; >>A=[12:11;31]; 10分 >>B=[161024]'; >>LB=[00]'; 12分 >>X,fual]=linprog(C,A,B,[],[],LB) 14分 13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 B B2 B 供应量 B B2 B 产地 B Bs A 50 250 400 700 3 5 6 1 A2 100 100 4 3 6 6 A 100 100 200 2 3 4 需求量 150 100 250 500 1000 12分 找空格对应的闭回路,计算检验数,直到出现负检验数: 2=3,A21=3,入2=3,入23=2,A33=-2 14分 已出现负检验数,方案需要调整,调整量为=100吨。 16分 1243
得惟一驻点 3吨。 故当运输量为 3吨时,利润最大。 最大利润为 .( 5万元。 12. 种产 为Xl 三0 maxS= Xl +2xz~16 线性规划模型为: I Xl +XZ 3Xl +XZ 2 4 计算该线性规划模型的 B命令语句为 »clear »C=-[3 4J; »A=[l 2;1 1;3 1]; »B=[16 10 24J »LB=[O OJ'; »[X 卢al]=linprog(C ,A ,B ,LE) 13. 下表 运输平衡表与运价表 12 13 14 10 12 14 泣导 Bl B2 B3 B4 供应量 Bl B2 B3 B4 Al 50 250 400 700 3 5 6 7 A2 100 100 4 3 6 5 A3 100 100 200 2 1 3 4 需求量 150 100 250 500 1000 12 找空格对应的闭回路,计算检验数,直到出现负检验数 A12 =3 ,λ21 =3 ,λ22 =3 ,Az3 =2 已出现负检验数,方案需要调整,调整量为 0吨。 14 16 1243
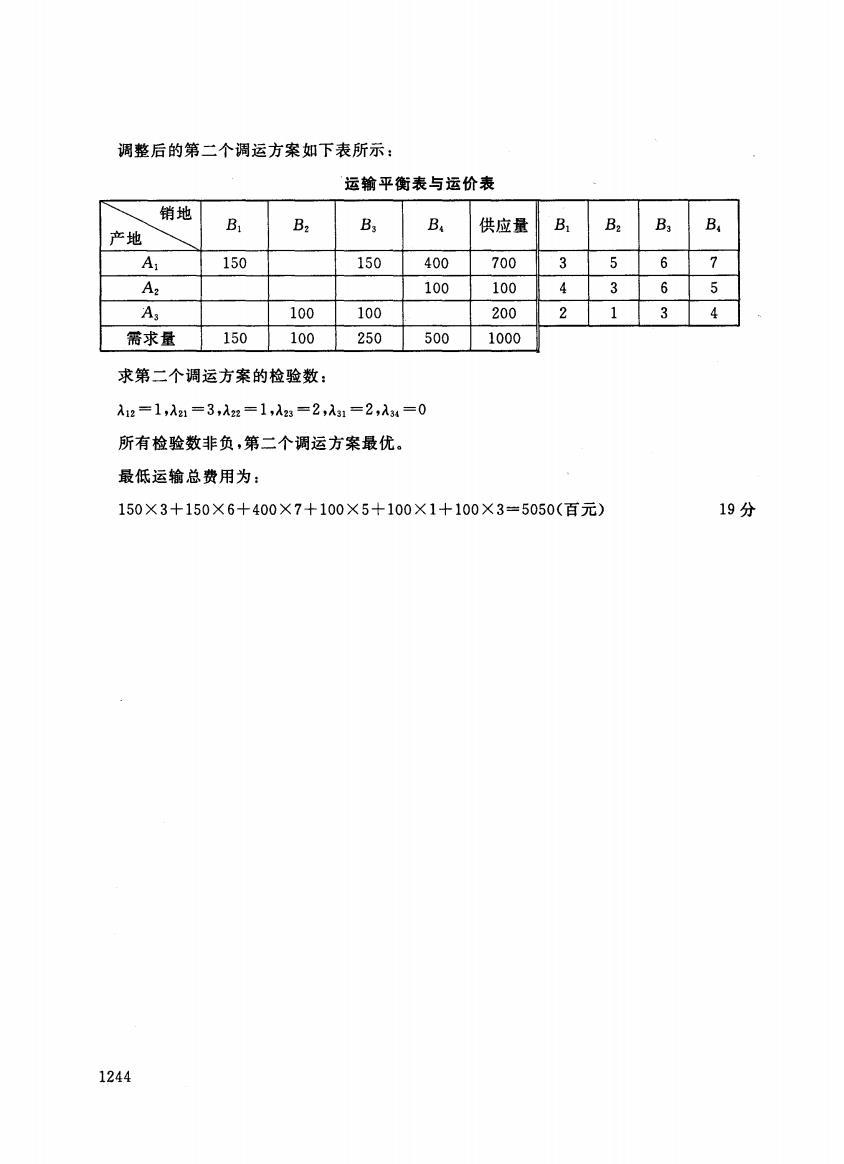
调整后的第二个调运方案如下表所示: 运输平衡表与运价表 销地 B B2 B, B 供应量 B B2 B3 B. 产地 A 150 150 400 700 3 5 6 7 A2 100 100 4 3 6 5 A3 100 100 200 2 1 3 4 需求量 150 100 250 500 1000 求第二个调运方案的检验数: λ12=1,λ21=3,入22=1,λ23=2,入31=2,入34=0 所有检验数非负,第二个调运方案最优。 最低运输总费用为: 150×3+150×6+400×7+100×5+100×1+100×3=5050(百元) 19分 1244
调整后的第二个调运方案如下表所示: 运输平衡表与运价表 泣可 B1 B2 B3 B4 供应量 B1 B2 B3 B4 Al 150 150 400 700 3 5 6 7 A2 100 100 4 3 6 5 A3 100 100 200 2 1 3 4 需求量 150 100 250 500 1000 求第二个调运方案的检验数 )\12=1 ').21 =3').22 = 1 ').23 =2 ').31 =2').34 =0 所有检验数非负,第二个调运方案最优。 最低运输总费用为 150 X 3+150 X 6+400 X 7+100 X 5+100 Xl + 100 X 3=5050( 1244 19