试卷代号:2320 座位号■■ 中央广播电视大学2009一2010学年度第一学期“开放专科”期末考试 物流管理定量分析基础 试题 2010年1月 题 号 三 四 总 分 分数 得分 评卷人 一、单项选择题:(每小题4分,共20分) 1.下列问题(供应量、需求量单位:吨,单位运价单位:元/吨)是( )运输问题。 供需量数据表 销地 I Ⅱ Ⅲ 供应量 产地 A 15 17 19 80 B 22 14 16 50 需求量 30 60 40 A.供求平衡 B.供过于求 C.供不应求 D.无法确定 2.某物流企业用甲、乙两种原材料生产A,B,C三种产品。企业现有甲原料30吨,乙原料 50吨。每吨A产品需要甲原料2吨;每吨B产品需要甲原料1吨,乙原料2吨;每吨C产品需 要乙原料4吨。又知每吨A,B,C产品的利润分别为3万元、2万元和0.5万元。为列出获得 最大利润的线性规划问题,设生产A,B,C三种产品的产量分别为x1吨、x2吨和x3吨,则目 标函数为()。 A.maxS=30x1+50x2 B.minS=3x1+2x2+0.5x3 C.minS=30x1+50.x2 D.maxS=3x1+2x2+0.5x3 1643
试卷代号:2320 座位号巨口 中央广播电视大学2009-2010学年度第一学期“开放专科”期末考试 物流管理定量分析基础 试题 2010年 1月 题 号 四 总 分 分 数 得 分 评卷人 一、单项选择题:(每小题 4分,共 20分) 1.下列问题(供应量、需求量单位:吨;单位运价单位:元/吨)是( )运输问题 。 据表 m -19 -16 -40 \、\ 、、、销地 }i 1 严 地 、、、 } 需 皿 n 供应量 80 -50 A B 需求量 A.供求平衡 C.供不应求 B.供过于求 D.无法确定 2.某物流企业用甲、乙两种原材料生产 A,B,C三种产品。企业现有 甲原料 30吨,乙原料 50吨。每吨A产品需要甲原料 2吨;每吨B产品需要甲原料 1吨,乙原料 2吨;每吨C产品需 要乙原料 4吨。又知每吨 A,B,C产品的利润分别为 3万元、2万元和 0. 5万元。为列出获得 最大利润的线性规划问题,设生产 A,B,C三种产品的产量分别为 x1吨、x:吨和 x3吨,则目 标函数为( )。 A. maxS=30x, -1-50x2 B. minS=3x1 +2x2 -}-0. 5x3 C. minS=30x1 +50x2 D. maxS=3x, +2x2 +0. 5x3 1643

1001 3.矩阵A= 0 00 ,不是()。 001 A.单位矩阵 B.对角矩阵 C.三角矩阵 D.对称矩阵 4.设某公司运输某物品的总收人(单位:千元)函数为R(q)=100q一0.2q,则运输量为 100单位时的总收入为( )千元/单位。 A.40 B.60 C.80 D.8000 5.已知运输某物品q吨的边际成本函数(单位:元/吨)为MC(q)=100+4q,则运输该物 品从100吨到200吨时成本的增加量为()。 100 A. (100+4q)dq B.(100+4g)dg (100+4q)dg Dmo0+oid+co) 得分 评卷人 二、计算题:(每小题7分,共21分) 1 -107 1237 6.已知矩阵A= 0 11 ,B= 045,求:BrA -1 02 006 7.设y=(x2-3)lnx,求:y &.计算定积分:e+女 得 分 评卷人 三、编程题(每小题6分,共12分)】 9.试写出用MATLAB软件计算函数y=c 2十x 的二阶导数的命令语句。 10.试写出用MATLAB软件计算不定积分x'Inxdx的命令语句。 1644
不 是 们 | 川 日 J 划 几 | 卜旧.| 陌 ﹂ A 一一 0 矩 阵 d A.单位矩阵 B.对角矩阵 C.三角矩阵 D.对称矩阵 4.设某公司运输某物品的总收人(单位:千元)函数为R(妇=100q-0. 2矿,则运输量为 100单位时的总收人为( )千元/单位。 A. 40 B. 60 C. 80 D. 8000 5.已知运输某物品4吨的边际成本函数(单位:元/吨)为 MC <妇=10。十4q,则运输该物 品从 100吨到 200吨时成本的增加量为( )。 ^·丁:::< 100+4q) dq C丁:::(100+4q) dq B.丁(100-4q)dq D丁:::(100-}4q)dq十C(0) 得 分 评卷人 二、计算题:‘每小题 7分.共 21分) BTA 求 一引 | .别 | 引 ﹂ 几 1-. 10 | | 旧 . B -- 们 | 1川 | 川 ﹂ 「‘一‘ 6.已知矩阵A=} 匕 0 I 0 ‘ 7.设 y= (x2一3) In x,求:y 8·计算定积分;户e} }-专)dx, 得 分 评卷人 三、编程题(每小题 6分 ,共 12分) 9.试写出用 MATLAB软件计算函数 y=在 e=Z 2-f-x 的二阶导数的命令语句。 10·试写出用MATLA”软件计算不定积分丁x3lnxd二的命令语句。 1644
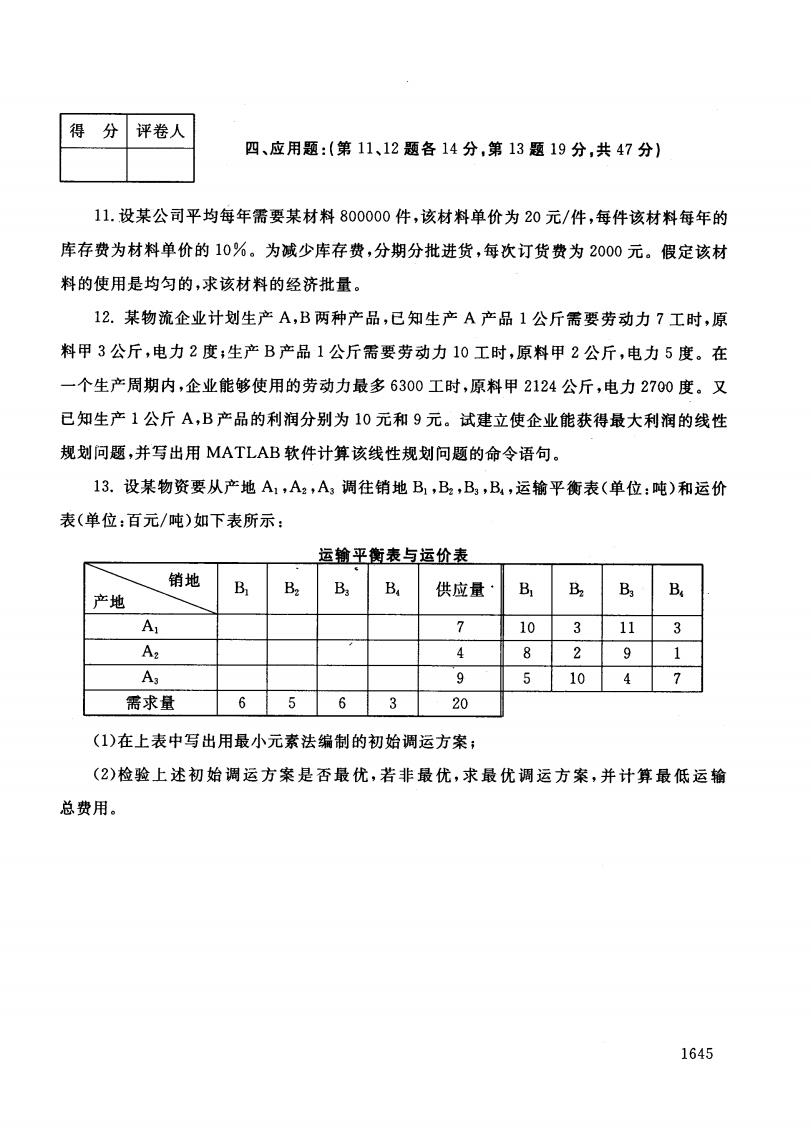
得分 评卷人 四、应用题:(第11、12题各14分,第13题19分,共47分) 11.设某公司平均每年需要某材料800000件,该材料单价为20元/件,每件该材料每年的 库存费为材料单价的10%。为减少库存费,分期分批进货,每次订货费为2000元。假定该材 料的使用是均匀的,求该材料的经济批量。 12.某物流企业计划生产A,B两种产品,已知生产A产品1公斤需要劳动力7工时,原 料甲3公斤,电力2度;生产B产品1公斤需要劳动力10工时,原料甲2公斤,电力5度。在 一个生产周期内,企业能够使用的劳动力最多6300工时,原料甲2124公斤,电力270度。又 已知生产1公斤A,B产品的利润分别为10元和9元。试建立使企业能获得最大利润的线性 规划问题,并写出用MATLAB软件计算该线性规划问题的命令语句。 13.设某物资要从产地A1,A2,A3调往销地B1,B2,B,B4,运输平衡表(单位:吨)和运价 表(单位:百元/吨)如下表所示: 运输平衡表与运价表 销地 B B2 Ba B 供应量· B B2 Ba B 产地 A 7 10 3 11 3 A2 4 8 2 9 1 A 9 5 10 4 需求量 6 5 6 3 20 (1)在上表中写出用最小元素法编制的初始调运方案; (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输 总费用。 1645
得 分 评卷人 四、应用题:(第 11,12题各 14分.第 13题 ” 分,共 47分) 11.设某公司平均每年需要某材料 800000件,该材料单价为 20元/件,每件该材料每年的 库存费为材料单价的 1000。为减少库存费,分期分批进货,每次订货费为 2000元。假定该材 料的使用是均匀的,求该材料的经济批量。 12.某物流企业计划生产 A,B两种产品 ,已知生产 A产 品 1公斤需要劳动力 7工时,原 料甲3公斤,电力 2度;生产 B产品 1公斤需要劳动力 10工时,原料甲 2公斤,电力 5度。在 一个生产周期内,企业能够使用的劳动力最多 6300工时,原料甲2124公斤,电力 2700度。又 已知生产 1公斤 A,B产品的利润分别为 10元和 9元。试建立使企业能获得最大利润的线性 规划问题,并写出用 MATLAB软件计算该线性规划问题的命令语句。 13.设某物资要从产地 A, AZ , A3调往销地 Bi } BZ , B3残,运输平衡表(单位:吨)和运价 表(单位 :百元/吨)如下表所示 : (1)在上表中写出用最小元素法编制的初始调运方案; (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输 总费用。 1645

试卷代号:2320 中央广播电视大学2009一2010学年度第一学期“开放专科”期末考试 物流管理定量分析基础试题答案及评分标准 (供参考) 2010年1月 一、单项选择题(每小题4分,共20分) 1.A 2.D 3.A 4.D 5.C 二、计算题(每小题7分,共21分) 0 0「1 -10「1-101 6.BTA= 1 1=2 24 7分 2-3217 7.y=(x2-3)'·lnx+(x2-3)·(lnx)'=2xlnx+x-3 7分 8.(e+)dz=(e+Inlzl)-e-e+ln2 7分 三、编程题(每小题6分,共12分) 9. >clear; >>syms x y; 2分 >>y=sqrt(x)*exp(x^2)/(2+x); 4分 >>dy=diff(y,2) 6分 10. >>clear; >>syms x yi 2分 >>y=xn3¥log(x): 4分 >>int(y) 6分 四、应用题(第11、12题各14分,第13题19分,共47分) 11.库存总成本函数为: C(g)=号×20×10%+80000×200=g+16000000 8分 q q 令C'(g)=1-1600000000=0得定义域内的惟一驻点q=40000件。 12分 即经济批量为40000件。 14分 1646
试卷代号:2320 中央广播电视大学2009-2010学年度第一学期“开放专科”期末考试 物流管理定量分析基础 试题答案及评分标准 (供参考) 2010年 1月 一、单项选择题 (每小题 4分,共 20分 ) l. A 二、计算题 【每小题 2. D 7分 .共 21 3.A 4. D 5. C 分》 一 1 一 1 分 分 月/ 月了 “」 n‘d } 4 }}} 1 上 9 口 1 尸十 ‘.! 卜 L -一 -训 ‘川 划 川 剑 曰 阮 卜 L 们 | 川 | 剑 自卜卜 咫 乡卜旧 ﹄ 产O B rA -- 7. y'= 10. >> clear; ; syms x y; ; y=x八3,log( x); ; int(y) 四、应用题 (第 11,12题各 14分 .第 13题 19分 ,共 47分 ) 11.库存总成本函数为: C<q)= 2 X 20 X‘ 。%+缨 X 200。一、+ 1600000000 4 令C'(q)=1一 即经济批量为 1646 1600000000 gz 40000件 。 =0得定义域内的惟一驻点q= 40000件。 8分 12分 14分
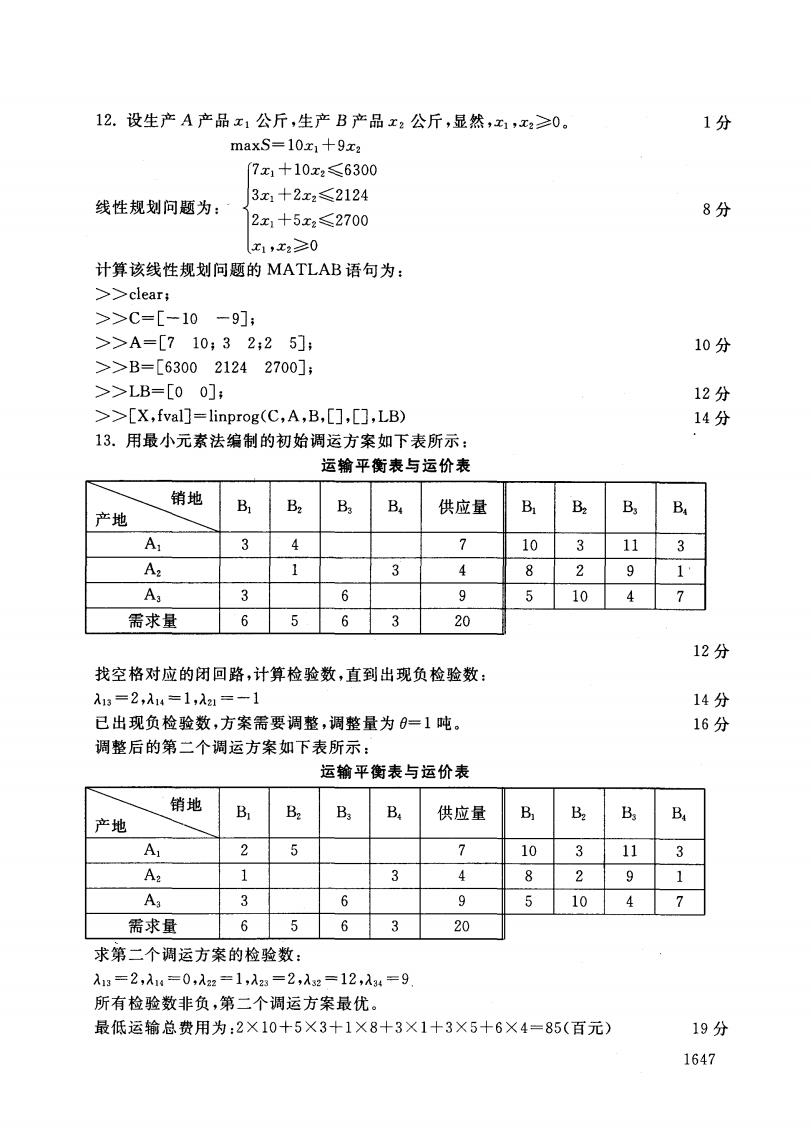
12.设生产A产品x1公斤,生产B产品x2公斤,显然,x1,x2≥0。 1分 maxS=10x1+9x2 7x1十10x2≤6300 3x1十2x2≤2124 线性规划问题为: 2x1+5x2≤2700 8分 x1,x2≥0 计算该线性规划问题的MATLAB语句为: >>clear; >>C=[-10-9]; >>A=[710;32:25]; 10分 >>B=[630021242700]; >>LB=[00]: 12分 >>[X,fval]=linprog(C,A,B,[],],LB) 14分 13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 Br B2 B B. 供应量 Bi B2 B B 产地 A 3 4 7 10 3 11 3 A2 1 3 4 8 2 9 1 A3 3 6 9 5 10 4 7 需求量 6 5 6 3 20 12分 找空格对应的闭回路,计算检验数,直到出现负检验数: 入13=2,入14=1,A21=-1 14分 已出现负检验数,方案需要调整,调整量为=1吨。 16分 调整后的第二个调运方案如下表所示: 运输平衡表与运价表 销地 Bi B2 Ba Ba 供应量 B B2 B3 B 产地 A 2 7 10 3 11 3 A2 1 3 4 8 2 9 1 Aa 3 6 9 5 10 需求量 6 5 6 3 20 求第二个调运方案的检验数: λ13=2,入14=0,入22=1,λ23=2,λ32=12,λ34=9 所有检验数非负,第二个调运方案最优。 最低运输总费用为:2×10+5×3十1×8+3×1+3×5+6×4=85(百元) 19分 1647
12.设生产A产品x1公斤,生产 B产品x:公斤,显然,x1 , xz >O o maxS=10x1+9xz 1分 n U O A 人 八U , 口 Q 目 ︸日 ︼ 内b l l tl 镇 貂 貂 衫 镇 镇 10 加 孙 妻 + + + 赴 7x 3x Zx xl f | | 卜 K | 卜 | 七 线性规划问题为: 计算该线性规划问题的 MATLAB语句为: ; clear; ; C=[一10 一9]; ; A=[7 10;3 2;2 5]; > > B = [6300 2124 2700]; ; LB=[0 0]; ; [X,fval]=linprog(C,A,B,[〕,[〕,LB) 13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 8分 10分 12分 14分 落}矿}}}Bl Bz B3 Bq 供应量一 残 Bg Bq A1 3 4 7 }10 3 11 3 AZ 1 3 4 }一 2 9 1、 A, 3 6 9 }一 5 10 4 7 需求量 6 5 6 3 20 {} 12分 找空格对应的闭回路,计算检验数,直到出现负检验数: }13=2从14“1,.i2i=一1 已出现负检验数,方案需要调整,调整量为B=1吨。 调整后的第二个调运方案如下表所示 : 运输平衡表与运价表 14分 16分 七 ) J卜出 涟、地、、 B, Bz B3 B4 供应量一B} }Z }3 l4 A, 2 5 7 }10 3 11 3 AZ 1 3 4 {8 2 9 1 A3 3 6 9 }5 10 4 7 需求量 6 5 6 3 2Q } 求第二个调运方案的检验数: n13=2,}1ia=0,}zz=1}}23-2f}32-12fA34=9. 所有检验数非负 ,第二个调运方案最优。 最低运输总费用为 :2X10十5 X 3- 1 X 8+3 X 1+3 X 5+6 X 4=85(百元) 19分 1647