
Lecture 4-2 Biomedical Applications of AR Model Prof.N Rao
Lecture 4-2 Biomedical Applications of AR Model Prof. N Rao

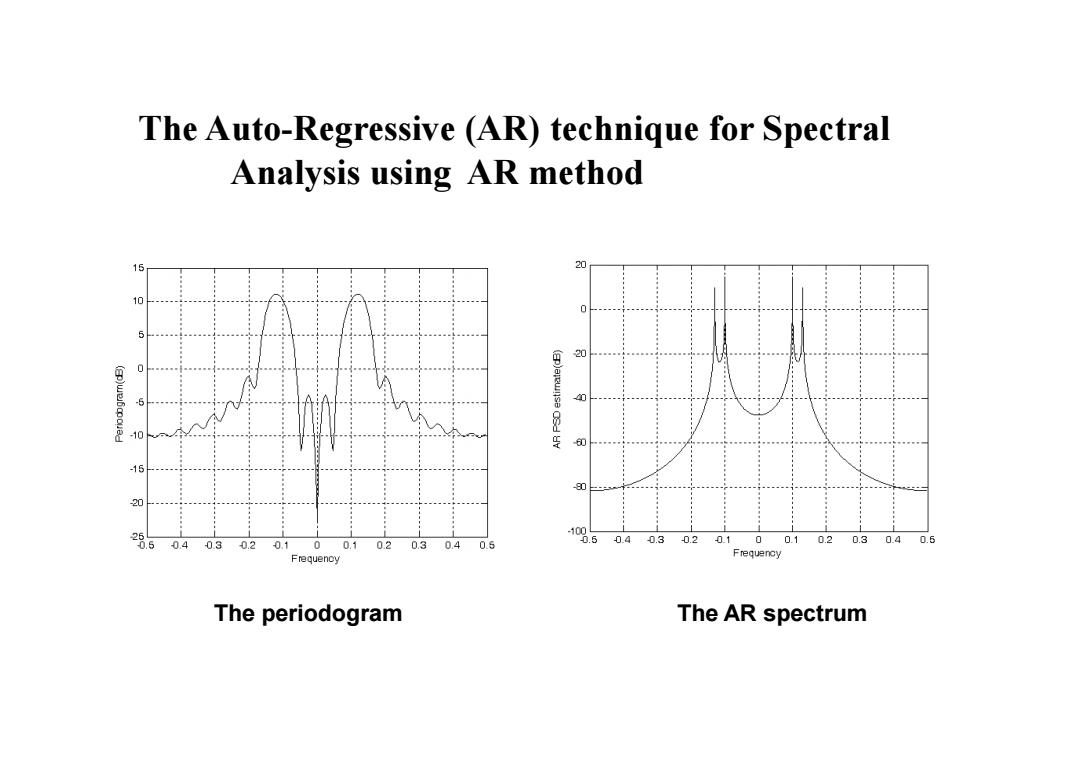
The Auto-Regressive (AR)technique for Spectral Analysis A numerical example: (n)=√2cos(2π(0.1)n)+V2cos(2π(0.13)n)+o(n) where n=0,1,...,(N-1)and w(n)is white Gaussian noise with variance 10-. Taking N=19
The Auto-Regressive (AR) technique for Spectral Analysis A numerical example: where n = 0,1,…, (N-1) and ω ( n) is white Gaussian noise with variance = 10-6 . Taking N = 19. x ( n ) = 2 cos( 2 π ( 0.1 ) n ) + 2 cos( 2 π ( 0.13 ) n ) + ω( n )
The Auto-Regressive (AR)technique for Spectral Analysis using aR method 15 20 10 1 -100 0.50.40.3 0.2 00.10.20.30.40.5 0.4 0.3 0.2 0.1 0 0.1 0.2 0.30.40.6 01 Frequenoy Frequency The periodogram The AR spectrum
The Auto-Regressive (AR) technique for Spectral Analysis using AR method The periodogram The AR spectrum

It can clearly be seen from Figure 1 that the AR technique exhibits superior resolution.It has distinguished the two sinusoids even though they are very closely spaced in frequency. The periodogram cannot resolve the signals because their spacing is 0.03 cycles/sample which would require a data record of at least N=1/0.03 34 points. In addition,note the smoothness of the AR spectrum which exhibits fewer random fluctuations due to noise and statistical estimation errors as well as an absence of sidelobes.Having justified the advantages of the AR model,we now describe it and its use
• It can clearly be seen from Figure 1 that the AR technique exhibits superior resolution. It has distinguished the two sinusoids even though they are very closely spaced in frequency. • The periodogram cannot resolve the signals because their spacing is 0.03 cycles/sample which would require a data record of at least N = 1/0.03 = 34 points. • In addition, note the smoothness of the AR spectrum which exhibits fewer random fluctuations due to noise and statistical estimation errors as well as an absence of sidelobes. Having justified the advantages of the AR model, we now describe it and its use

Homework4:取19点和多于34点,用周期图方法和 AR模型方法观察下列信号的功率谱,并作对比分析。 x(n)=V2cos(2π(0.1)n)+√2cos(2π(0.13)n)+on)
x(n) = 2 cos(2π (0.1)n) + 2 cos(2π (0.13)n) + ω(n) Homework 4: 取19点和多于34点,用周期图方法和 AR模型方法观察下列信号的功率谱,并作对比分析
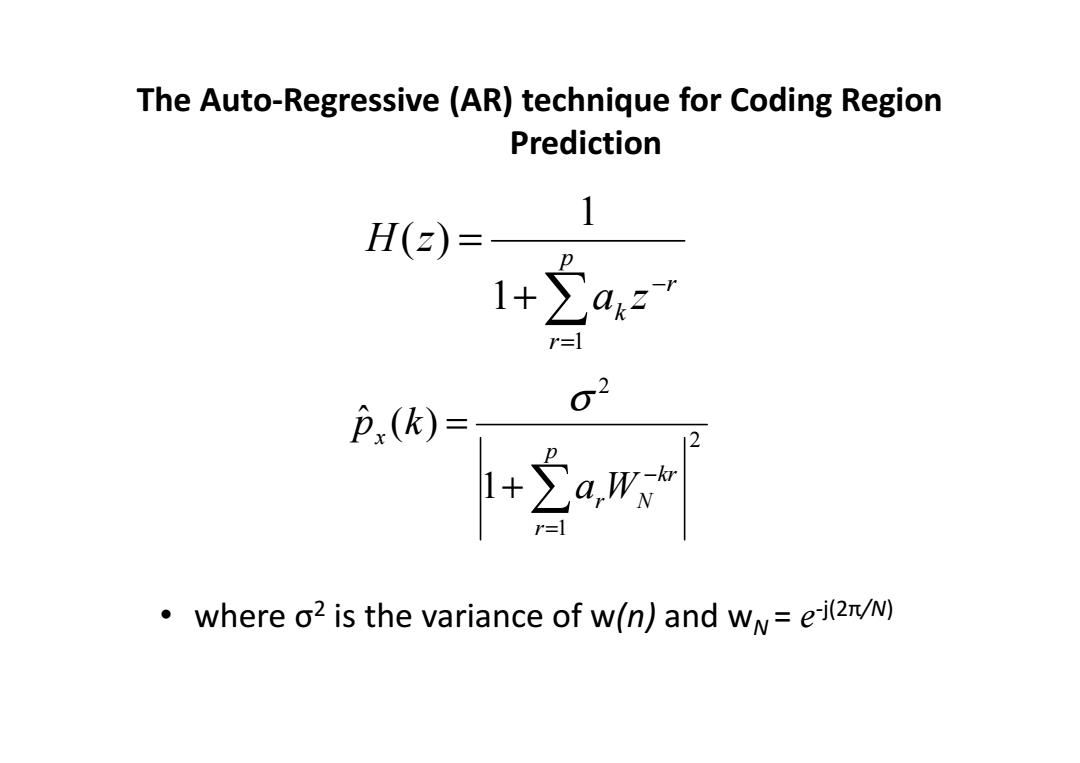
The Auto-Regressive (AR)technique for Coding Region Prediction 1 H(z)= 1+a2 02 P(k)= E where o2 is the variance of w(n)and w=ei(z/N)
The Auto-Regressive (AR) technique for Coding Region Prediction • where σ 2 is the variance of w(n) and w N = e -j(2π/N) ∑= − + = p r r k a z H z 1 1 1 ( ) 2 1 2 1 ˆ ( ) kr N p r r x a W p k − = + ∑ = σ

Experimental Scheme The spectral analysis methods have been applied to various genomic sequences from several different organisms and the results compared: Fast Fourier Transform(FFT)periodogram, AR model using the Burg algorithm with p=30(called Burg 1) AR model using the Burg algorithm with p=50(called Burg 2) AR model based on the improved covariance analysis with p=30 (called Cov.1) AR model based on the improved covariance analysis with p=50 (called Cov.2)
Experimental Scheme The spectral analysis methods have been applied to various genomic sequences from several different organisms and the results compared: • Fast Fourier Transform (FFT) periodogram, • AR model using the Burg algorithm with p = 30 (called Burg 1) • AR model using the Burg algorithm with p = 50 (called Burg 2) • AR model based on the improved covariance analysis with p = 30 (called Cov. 1) • AR model based on the improved covariance analysis with p = 50 (called Cov. 2)

Experimental Scheme In order to assess and compare the different methods,the local signal to noise ratio P(dB)is defined as: 10*1gs,(3) P= S1
Experimental Scheme • In order to assess and compare the different methods, the local signal to noise ratio P (dB) is defined as: ( ) f f S S P 3 1 10 * lg =

Experimental Results ·Large DNA sequences (more than 10000 base pairs) Method I FFT Burgl B12 Co.1 Cov.2 F 5.0048 6.80869.54296.79919.5431
Experimental Results • Large DNA sequences (more than 10000 base pairs )

Experimental Results ·Medium DNA sequences (between 3000 and 10000 base pairs) Method FFT Burgl Bug2 Cov.1 Cov.2 P 281487.834010.81077.758310.6904
Experimental Results • Medium DNA sequences (between 3000 and 10000 base pairs)