
Lecture 5-1 Kalman Filter Prof.N Rao
Lecture 5-1 Kalman Filter Prof. N Rao

1.Introduction The features of AR Parameter Model and Wiener Filter: (1)be suitable to process stationary random signals (2)The prior statistical property knowledge for signals and noise is required (3)The parameters of filter system are fixed 2
2 The features of AR Parameter Model and Wiener Filter: (1)be suitable to process stationary random signals (2)The prior statistical property knowledge for signals and noise is required (3)The parameters of filter system are fixed 1. Introduction

(1)Be suitable to process non-stationary random signals (2)The prior statistical properties for signals and noise are required; 3 The parameters of the filter are time-variation. 3
3 (1)Be suitable to process non-stationary random signals; (2)The prior statistical properties for signals and noise are required; (3)The parameters of the filter are time-variation

3.卡尔曼滤波器的信号模型及算法 一离散状态方程与量测方程 卡尔曼滤波器的信号模型是由状态方程和量测方程得到的。离散时间系统的 状态方程定义为: x(k+1)=Ax(k)+Be(k) (3-1) 式中x(k)表示一组状态变量组成的多维状态变量,(k)是激励信号,A、B都是系 统的结构确定的矩阵。 当己知初始状态x(O),可用递推方法得到它的解x(k): x(1)=Ax(O)+Be(0) x(2)=Ax(1)+Be(1)=A2x(0)+ABe(0)+Be(1) (3-2) =4x0+24BaU刀 =0 在式(3-2)中,等式右边第一项只与初始状态和系统结构有关,与激励(·)无关, 故称为零输入响应;第二项与初始状态无关,只与激励和系统结构有关,故称 零状态响应
3. 卡尔曼滤波器的信号模型及算法 —离散状态方程与量测方程 零状态响应。 故称为零输入响应;第二项与初始状态无关,只与激励和系统结构有关,故称为 在式 中,等式右边第一项只与初始状态和系统结构有关,与激励 无关, 当已知初始状态 ,可用递推方法得到它的解 统的结构确定的矩阵。 式中 表示一组状态变量组成的多维状态变量, 是激励信号, 、 都是系 ) 状态方程定义为: 卡尔曼滤波器的信号模型是由状态方程和量测方程得到的。离散时间系统的 (3 2) ( ) ( ) (0) ( ) ... (2) )1( )1( (0) (0) )1( )1( (0) (0) (0) ( :) ( ) ( ) ( 1 ( ) ( ) 1 0 1 2 − • = + = + = + + = + + = + ∑−= − − e x k A x A Be j x Ax Be A x ABe Be x Ax Be x x k x k e k A B x k Ax k Be k k j k k i (3-1) (3-2)

3.卡尔曼滤波器的信号模型及算法 一离散状态方程与量测方程 从状态转移到一步递推 令Φ(k)=A,并代入式(3-2)得 k)=ΦkxO)+(k-1-)Be (3-3) j=0 当(k)=0时,x()=(k)x(O)=Ax(O)。通过A,可将k=0时的状态过渡到任何k>0 的状态,故称Φ(k)为转移矩阵或过渡矩阵。当己知x(O),激励()以及A、B矩阵,就 可以根据式(3-3)求得x(k)的解。若用ko表示k的起始值,则式(3-3)从x(ko)开始递推, 会有 k-1 因=中60)+∑kH1BeU) (3-4) i=ko 式中Φkk,表示从ko状态到k状态的转移矩阵。若k,=k-1,就可以得到一步递推公式 x(k)=Φkk-1x(k-l)+Φ(O)Be(k-1) (3-5)
3. 卡尔曼滤波器的信号模型及算法 —离散状态方程与量测方程 从状态转移到一步递推 ( ) ( )1 )0( ( )1 1 ( ) ( ) ( ) 3( )3 ( ) 3( )3 ( ) ( ) )0( ( ) ( ) 0 ( ) ( ) )0( )0( 0 0 ( ) ( ) )0( ( 1 ) ( ) ( ) , 3( )2 , 1 , 0 0 1 , 0 , 1 0 0 1 0 0 0 0 = Φ − + Φ − Φ = − = Φ + Φ − − Φ = = Φ = = > = Φ + Φ − − Φ = − − −= + −=∑∑ x k x k Be k k k k k x k x k Be j x k k k x k k x e j A B e k x k k x A x A k k x k k x k j Be j k A k k k k kj k k k k j k k kj k 式中 表示从 状态到 状态的转移矩阵。若 ,就可以得到一步递推公式 会有可以根据式 求得 的解。若用 表示 的起始值,则式 从 开始递推, 的状态,故称 为转移矩阵或过渡矩阵。当已知 ,激励 以及 、 矩阵,就 当 时, 。通过 ,可将 时的状态过渡到任何 令 并代入式 得 (3-3) (3-4) (3-5)

3.卡尔曼滤波器的信号模型及算法 一一离散状态方程与量测方程 一步递推状态方程 由于Φ(O)=A=1,代入上式得由于Φ(0)=A=1,代入上式得 x(k)=Φk.k-1x(k-1)+B(k-1) (3-6) 假设激励源为白噪声,即B(k-1)=w(k-1)称为系统动态噪声,而系统是时变的,即 Φk.k-1=A(k),则式(3-6)又可写成 x(k)=Ak)x(k-1)+w(k-1) (3-7) 为了书写方便,将变量k放在下标表示,则上式为 x(k)=Akxk-1+Wk-1 (3-8) 式(3-8)表明k时刻的状态x(k)可由它前一时刻状态x(k-1)来求得,故该式又称为一步 递推状态方程
3. 卡尔曼滤波器的信号模型及算法 ——离散状态方程与量测方程 一步递推状态方程 递推状态方程。 式 表明 时刻的状态 可由它前一时刻状态 来求得,故该式又称为一步 为了书写方便,将变量 放在下标表示,则上式为 ,则式 又可写成 假设激励源为白噪声,即 称为系统动态噪声,而系统是时变的,即 由于 ,代入上式得由于 ,代入上式得 3( )8 ( ) ( )1 ( ) ( ) ( ) ( )1 ( )1 ( ) 3( )6 ( )1 ( )1 ( ) ( )1 ( )1 )0( 1 )0( 1 1 1 , 1 , 1 0 0 − − = + = − + − Φ = − − = − = Φ − + − Φ = = Φ = = − − − − k x k x k x k A x w k x k A k x k w k A k Be k w k x k x k Be k A A k k k k k k k (3-6) (3-7) (3-8)

卡尔曼滤波需要依据观测数据对系统状态进行估计,因此,除了要建立系统的状态 方程,还需要建立一个量测方程。一般假设观测系统是线性的,对于离散时间系统的量 测方程可以写成下式 yk=Ckxk+Vk (3-9) 式中yk为观察或量测到的信号矢量序列,vk为观测噪声序列,ck是观测矩阵(m×)m为 y的维数,n为v的维数,ckx是信号真值,它是状态变量x各分量的线性组合,即 Sk=Ckxk (3-10) 将式(3-10)代入式(3-9),得 yk=Sk +Vk (3-11) 上式的含义是,我们观察或量测到的信号y包括信号的真值与噪声;式(3-11)中的信号 真值是一个多维矢量,从式(3-10)可见,它是状态变量x各分量的线性组合
真值是一个多维矢量,从式 可见,它是状态变量 各分量的线性组合。 上式的含义是,我们观察或量测到的信号 包括信号的真值与噪声;式 中的信号 将式 代入式 ,得 的维数, 为 的维数, 是信号真值,它是状态变量 各分量的线性组合,即 式中 为观察或量测到的信号矢量序列, 为观测噪声序列, 是观测矩阵 , 为 测方程可以写成下式 方程,还需要建立一个量测方程。一般假设观测系统是线性的,对于离散时间系统的量 卡尔曼滤波需要依据观测数据对系统状态进行估计,因此,除了要建立系统的状态 k k k k k k k k k k k k k k k k k k k k x y y s v s c x y n v c x x y v c m n m y c x v 3( 10) 3( 11) 3( 10) 3( )9 ( ) − − = + − − = × = + (3-9) (3-10) (3-11)

在维纳滤波中我们希望得到s(m)的估计值n与真值m)间的均方误差最小。在卡尔 曼滤波中,我们希望得到x的估计值与有最小均方误差。有了也就得到了飞。这 里信号表示为状态变量x的线性组合,是因为把待求的量表示为状态方程中的状态 变量线性组合具有很多优点,由于状态方程是一个一阶多维的方程,可以用一步递 推法求解。卡尔曼滤波相对于维纳滤波在计算上有很多优点,正是由于它利用了状 态方程得到的。 当与都是一维变量,且=1时,则有 y=xk+vk=Sk+V 此时卡尔曼滤波的测量方程与维纳滤波的信号方程x(m)=s(m)+m完全相 同。只是在符号上的表示所有差异罢了。在卡尔曼滤波公式中就是维纳 滤波中的x),它们都表示观察到的数据
在维纳滤波中我们希望得到 的估计值 与真值 间的均方误差最小。在卡尔 曼滤波中,我们希望得到 的估计值 与 有最小均方误差。有了 也就得到了 。这 里信号 表示为状态变量 的线性组合,是因为把待求的量表示为状态方程中的状态 变量线性组合具有很多优点,由于状态方程是一个一阶多维的方程,可以用一步递 推法求解。卡尔曼滤波相对于维纳滤波在计算上有很多优点,正是由于它利用了状 态方程得到的。 当 与 都是一维变量,且 时,则有 ns )( ˆ ns )( ns )( k x k x ˆ k x k s ˆ k x ˆ k yk x k x ck =1 k k k k k y = x + v = s + v 此时卡尔曼滤波的测量方程与维纳滤波的信号方程 完全相 同。只是在符号上的表示所有差异罢了。在卡尔曼滤波公式中 就是维纳 滤波中的 , 它们都表示观察到的数据。 nx )( = ns )( + nv )( nx )( k s ky
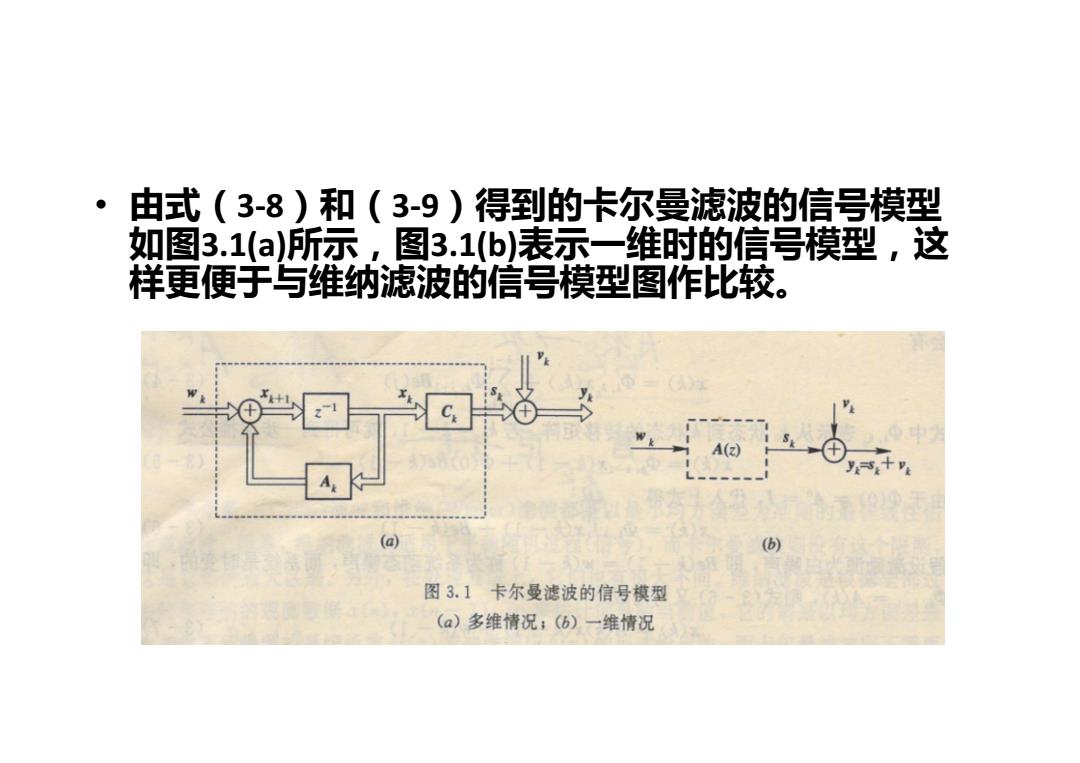
·由式(3-8)和(3-9)得到的卡尔曼滤波的信号模型 如图3.1(a)所示,图3.1(b)表示一维时的信号模型,这 样更便手与维纳滤波的信号模型图作比较。 A( (a) 图3.1卡尔曼滤波的信号模型 (a)多维情况;(b)一维情况
• 由式 (3-8)和(3-9)得到的卡尔曼滤波的信号模型 如图3.1(a)所示,图3.1(b)表示一维时的信号模型,这 样更便于与维纳滤波的信号模型图作比较

卡尔曼滤波器算法 我们要研究离散系统的维状态方程与维测量方程 (见式3-8)和3-11)),它们分别是: Xk=Akxk-1+Wk-1 yk=ckxk +V 假设动态噪声k与观测噪声vk都是均值为零的正态噪声,且两者互不相关,即 Elw:J=0.covw:.wJ=Ew:wjJ=Q:o Elv:]=0,cov[vs,v,J=EvevJ=R:op (3-12) covw:,vl=Ewy7]=0,k≠j,k,j=0,l2,… 式中Q=varw]=Eww称为动态噪声协方差阵, R=Var[y]=E[yv]为量测噪声协方差阵
见式( )和( )),它们分别是: 我们要研究离散系统的维状态方程与 维测量方程 ( 3-8 3-11 n m k k k k k k k k y c x v x A x w = + = −1 + −1 [ ] [ ] 为量测噪声协方差阵 式中 称为动态噪声协方差阵, var[ ] [ ] var T k k k k T k k k k R v E v v Q w E w w = = = = 卡尔曼滤波器算法 (3-12)