
二、 35 可别独立子体系的热力学函数 oas-N!IIg ni! In s In N! n11 多出一项InN! S=kIn N! +klnN! Nk In Q+ U F=-NkT In Q G=-NkT In Q+NkTV (V 72N

36 对于可别系,注意 (* 只有这三个函数的形式不同,其它热力 学量表达式中有微商,而InN!为常 数,无影响,所以: 对U,H,C。,Cv,粒子等同与否,其 表达式都相同

§3.5配分函数的计算及简单应用 37 一、配分函数的分离(因子分离) Q-Ze-8/kT j为状态编号,是对状态求和。 式中的能量8为一个粒子的能量,可 以分解为: 8=8t+8+8v+8e+8n 此式表明粒子的各种运动形态是独立 的,相互无影响,所有的量子态是各种 运动状态之和

38 Q=Σ(e8t/kT.e-&/kT .e-8/kT,e-8/kT.e-8n/kT) =(Ee-&/KT).(Ze-5/kT).(Ee-8/kT) (Ze-8c/kT).(e-8n/kT) =Q.[Q.Qv.Qe.Qn] QQ 一般情况下,乘积之和不等于和的 乘积,此处称之为独立变数乘积之和等 于各自求和的乘积,可以证明其正确

39 上面是对状态求和,若改为对能级 求和,需乘以g:。 Q,=e8aMT-=Σ8uekT Q,=Σe8kT-g.enkT Q,=2e8/kT=∑gve-Evi/kT Q。=Ee8gkT=Σ8ae8/kT Q-e-Su/kT-gne-Ea /eT 而且每种运动的粒子分布都符合 Boltzmann分布公式:

40 第ⅰ个平动能级上的粒子数为: Ngue-Et/kT n= Q 第j个转动能级上的粒子数为: N gne-Su/kT Q 其它用法类似,即: 各种运动可以独立考虑,各种运动对体 系热力学函数的贡献都是独立的
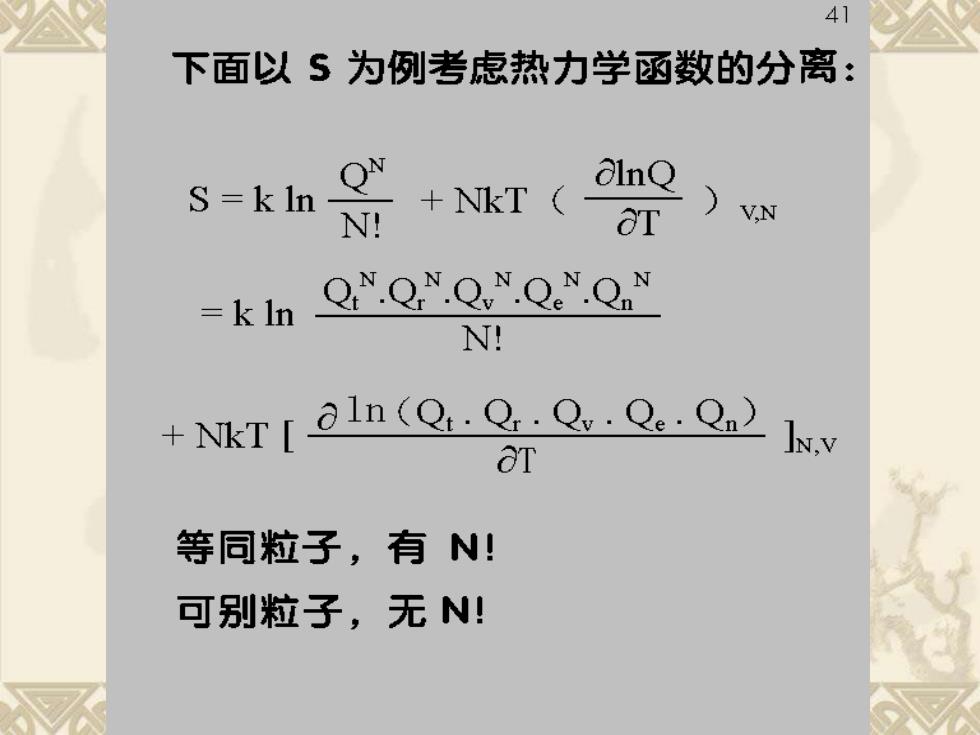
41 下面以5为例考虑热力学函数的分离: S=kIn Q OlnQ ! +NKT OT =k In QN.QN.QN.QNQ N! +NKT aln(Q.Q.Q。.Q.Q)kv ar 等同粒子,有N! 可别粒子,无N!

42 S=[k In InQ OT khQ+r(兴 )Nv]+ knQ+kT(号 ).v1+ in Q+NkT( in N.vl+ khQ+NT(ae)小 =S:+[S,+Sy+Se+Sn] =S+S1 S:外部运动熵,S:内部运动熵

说明: (1)N!体现等同粒子与可别粒子的差 别,等同粒子才有这一项,可别粒子无 这一项。只有平动才能使粒子成为离域 子,成为离域子才需要等同性修正。故 等同性修正只能在平动上进行,所以 N!这一项归于平动。其它各项不应有 等同行修正,也就没有N!这一项

44 (2)我们讨论的体系都是N固定的体 系,偏微分外的N下标可以不写,在所 有的运动中,只有平动与体积有关,其 余的与体积无关,因此后四项的偏微商 号可以直接写成全微商号,如 d inQ,d InQ 等等。 dT dT