
§2.11几个热力学函数间的关系 五个状态函数的关系: U,H,S,F,G 物理意义: 等TP,W=0,△H=Qp 等T,△F=-W可逆最大功 等TP,△G-W可逆最大非体积功 定义式:H=U+PV H F=U-TS U PV G-H-TS-U-TS+PV=F+PV TS F PV TS G
1 §2.11 几个热力学函数间的关系 五个状态函数的关系: U, H, S, F, G 物理意义: 等 TP,W`=0,ΔH=QP 等 T,ΔF=-W 可逆最大功 等 TP,ΔG=-W` 可逆最大非体积功 H U PV TS F PV TS G 定义式:H=U+PV F=U-TS G=H-TS=U-TS+PV=F+PV

1.基本热力学关系式 第一定律:dU=aQ-OW=aQ-PdV-OW 第二定律:OQ=TdS 可逆过程:OQ=OQ=TdS dU=Tds-PdV.∂W dH=d (U+PV)=dU+PdV+VdP TdS -PdV-OW+PdV+VdP dH=Tds+VdP-∂W
2 1. 基本热力学关系式 第一定律:dU= Q-W= Q-PdV- W` 第二定律: Qr =TdS 可逆过程: Q= Qr =TdS dU= TdS -PdV- W` dH=d(U+PV)=dU+PdV+VdP = TdS -PdV- W`+PdV+VdP dH= TdS +VdP - W` / /

dF=d (U-TS) =dU-Tds-SdT =Ts-PdV.∂W-Tds-SdT dlF=SdT-PdV.∂Wr dG=d (H-TS)=dH-Tds-SdT Tas +VaP-oW-Tas-SdT dG=-SdT+VdP-∂w 3
3 dF=d(U-TS) =dU-TdS-SdT = TdS -PdV- W`-TdS-SdT dF=-SdT-PdV- W` dG=d(H-TS)=dH-TdS-SdT = TdS +VdP - W`-TdS-SdT dG=-SdT+VdP - W` / / / /
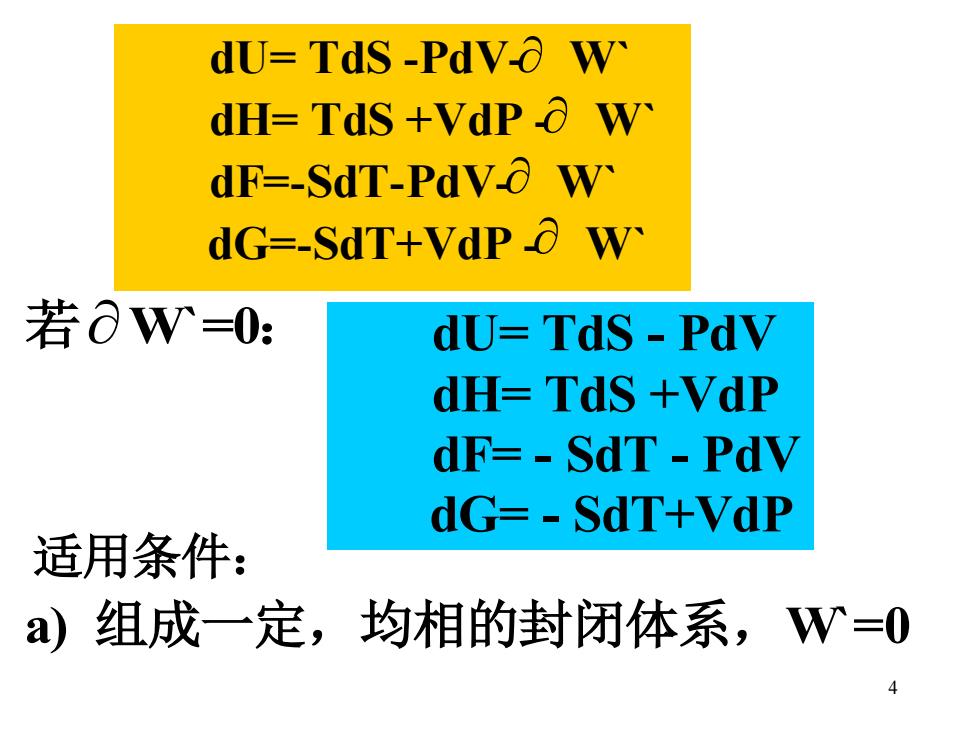
dU=TdS-PdVo W dH=TdS+VdPO W dF-SdT-PdVO W dG-SdT+VdP o W 若OW=0: dU=Tds-PdV dH=TdS +VdP dF=-SdT-PdV dG=-SdT+VdP 适用条件: a组成一定,均相的封闭体系,W=0
4 若W`=0: 适用条件: a) 组成一定,均相的封闭体系,W`=0 dU= TdS -PdV- W` dH= TdS +VdP - W` dF=-SdT-PdV- W` dG=-SdT+VdP - W` dU= TdS - PdV dH= TdS +VdP dF= - SdT - PdV dG= - SdT+VdP

b)状态变化:可逆和不可逆 相变和化学变化:只适用可逆过程 说明:a)对不可逆的状态变化,可以在不改 变原条件下可逆进行 b)相变和化学变化:设计可逆过程 例:-5℃H0(ID -5CP,R→-5℃H,0(g) 0℃H,O(I) 0CP,R→0℃HO(g)
5 b) 状 态 变 化:可逆和不可逆 相变和化学变化:只适用可逆过程 说明:a)对不可逆的状态变化,可以在不改 变原条件下可逆进行 b)相变和化学变化:设计可逆过程 例:- 5℃H2 O(l) ⎯− ⎯5C,P ⎯,IR→- 5℃H2 O(g) 0℃H2 O(l) ⎯0 ⎯C,P ⎯,R → 0℃H2 O(g)
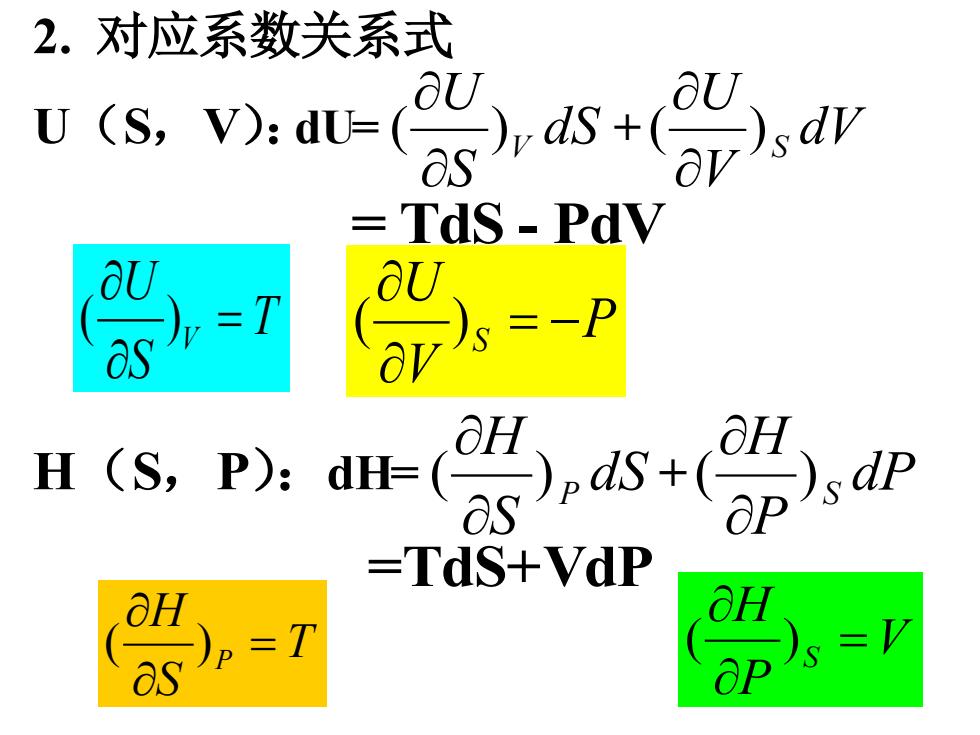
2.对应系数关系式 (5.vt- TdS-Pdv as =T Hs.P:r.s-(a0 H =TdS+VdP aH =7 =V as
6 2. 对应系数关系式 U(S,V):dU= dS S U V ( ) + dV V U S ( ) = TdS - PdV T S U V = ( ) P V U S = − ( ) H(S,P):dH= dS S H P ( ) + dP P H S ( ) =TdS+VdP T S H P = ( ) V P H S = ( )
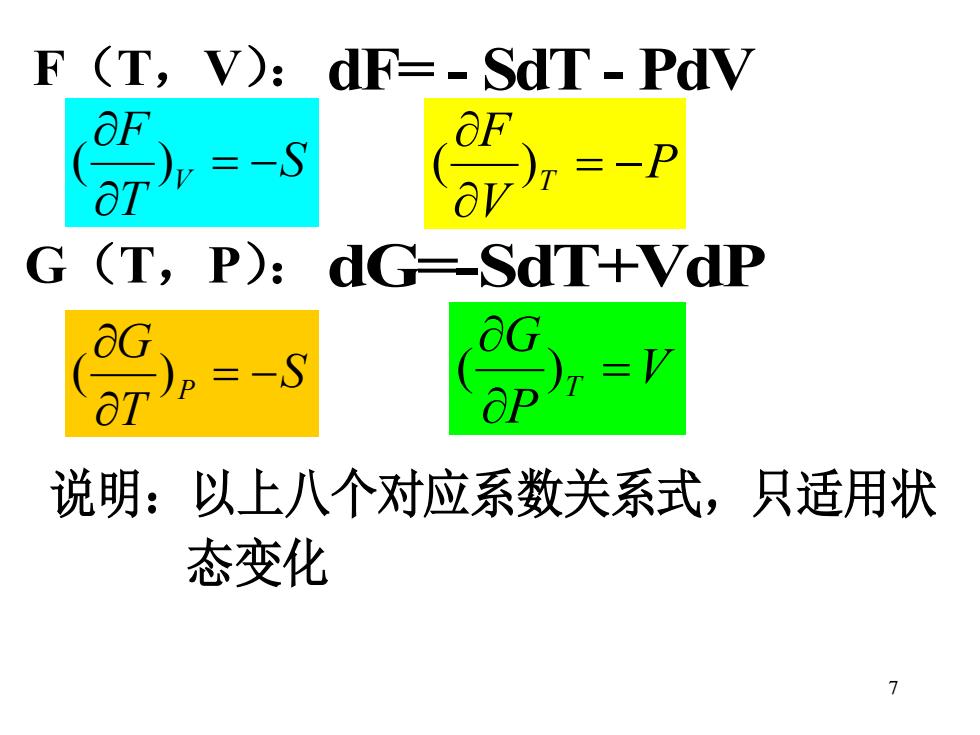
F (T,V):dF=-SdT-PdV G (T,P):dG-SdT+VdP -V 说明:以上八个对应系数关系式,只适用状 态变化 7
7 F(T,V): G(T,P): 说明:以上八个对应系数关系式,只适用状 态变化dF= - SdT - PdV dG=-SdT+VdP S T F V = − ( ) P V F T = − ( ) S T G P = − ( ) V P G T = ( )

3.特性函数 定义:如果选择适当的独立变量,只需一个 热力学函数,就可将均相体系的全部平衡性 质唯一确定出来,具有这种特性的热力学函 数称特性函数 特性函数:U(S,V),H(S,P) F (T,V),G(T,P) S(U,V),S(H,P),V(U,S),V(F,T) 非特性函数: U(T,V),U(P,S),U(T,P)
8 3. 特性函数 定义:如果选择适当的独立变量,只需一个 热力学函数,就可将均相体系的全部平衡性 质唯一确定出来,具有这种特性的热力学函 数称特性函数 特性函数:U(S,V),H(S,P) F(T,V),G(T,P) U(T,V),U(P,S),U(T,P) 非特性函数: S(U,V),S(H,P),V(U,S),V(F,T)

例:已知F(T,V)特性函数关系 可表示出体系其它平衡性质 dF=-SdT-PdV S (T,V) P (T,V) U-F+TS-F-T( U (T,V) 9
9 例:已知 F(T,V)特性函数关系 可表示出体系其它平衡性质 dF=-SdT-PdV S = - V T F ( ) S(T,V) P= - T V F ( ) P(T,V) U=F+TS =F-T V T F ( ) U(T,V)

H-U+PV-E.T(P)-V(P) H (T,V) 件PV=EV G(T,V 利用特性函数F(T,V): 确定:S(T,V),P(T,V), U(T,V),H(T,V),G (T,V) 利用特性函数G(T,P): 确定:S(T,P),V(T,P), U (T,P),H(T,P),G (T,P)o
10 H=U+PV= F-T V T F ( ) - V T V F ( ) H(T,V) G=F+PV=F- V T V F ( ) G(T,V) 利用特性函数 F(T,V): 确定:S(T,V),P(T,V), U(T,V),H(T,V),G(T,V) 利用特性函数 G(T,P): 确定:S(T,P),V(T,P), U(T,P),H(T,P),G(T,P)