§4-5相图边界理论及其应用 a L a M a2 T2 12 M2 S+L Si L+S2 C M E d S2 S1+S2 e XB→ B 图1典型的二元恒压相图 1
1 §4-5 相图边界理论及其应用

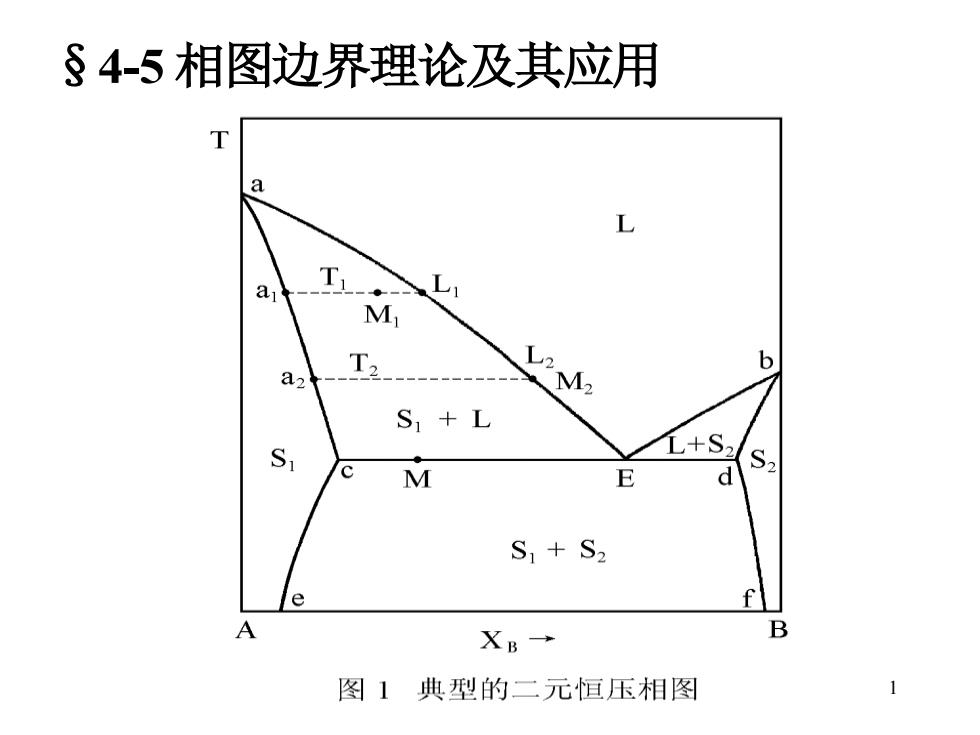
相图是由相区及其边界组成 如图1所示是一个典型的二元恒压相图 由五个边界点,六个相区,七条边界线组成 共用一条边界线或边界点的两个或几个相区 紧邻相区 研究相图构成的规律就是要研究紧邻相区 及其边界的关系 相律是相平衡中最主要的规律,但它不能 解决紧邻相区及其边界的关系问题
2 相图是由相区及其边界组成 如图 1 所示是一个典型的二元恒压相图 由五个边界点,六个相区,七条边界线组成 共用一条边界线或边界点的两个或几个相区 ——紧邻相区 研究相图构成的规律就是要研究紧邻相区 及其边界的关系 相律是相平衡中最主要的规律,但它不能 解决紧邻相区及其边界的关系问题

两个紧邻相区的共同边界细致地划分为边 界和相边界 1.边界定义: 是划分紧邻相区的体系点的集合 有的相图书籍把它叫几何边界 边界的维数用R'来表示 2.相边界定义: 是处于边界上,代表体系点的平衡相点的集合 相边界的维数以R表示 1981年首次提出相边界的概念 3
3 两个紧邻相区的共同边界细致地划分为边 界和相边界 1. 边界定义: 是划分紧邻相区的体系点的集合 有的相图书籍把它叫几何边界 边界的维数用 R1 ’来表示 2. 相边界定义: 是处于边界上,代表体系点的平衡相点的集合 1981 年首次提出相边界的概念 相边界的维数以 R1表示

问题:若一个体系的代表点恰好位于aE 线上,体系中只有一个均匀相还是 两个混合相呢? 相边界的概念是相图边界理论的核心 相图边界理论的推导中定义的物理量: 相边界维数为R,边界维数为R'1 体系的独立组元数或组分数为K 紧邻相区中不同的相的总数为Φ 紧邻相区中共同的相的数目为Φc
4 问题:若一个体系的代表点恰好位于 aE 线上,体系中只有一个均匀相还是 两个混合相呢? 相边界的概念是相图边界理论的核心 相图边界理论的推导中定义的物理量: 相边界维数为 R 1 , 边界维数为 R' 1 体系的独立组元数或组分数为 K 紧邻相区中不同的相的总数为Φ 紧邻相区中共同的相的数目为φC

可以证明,它们之间有如下关系: ①Φ和R的关系 R=K-Φ+1 (1) 对应关系定理 ②R和R1'的关系: 三相共存:R'=R+Φc (2) 在所有其它情况:R=R+Φc1 (3) 公式(1),(2),(3)就是恒压相图 边界理论的主要公式 5
5 可以证明,它们之间有如下关系: ①Φ和 R1的关系 R1 =K-Φ+1 (1) ——对应关系定理 ②R1和 R1 ’ 的关系: 三相共存:R1 ’ =R1 +φC (2) 在所有其它情况:R1 ’ =R1 +φC -1 (3) 公式(1),(2),(3)就是恒压相图 边界理论的主要公式

运用恒压相图边界理论: 1)可系统阐明不同类型相图的紧邻区间 及其边界关系 2)可推导国际上已有的关于紧邻相区及 边界关系的所有实验规则和理论法则 3)可以判断并改正某些实验相图的错误 4)可在实验数据不够下粗略勾画整个相图 5)可将相图边界理论和其它热力学理论 结合起来较快的计算相图
6 运用恒压相图边界理论: 1) 可系统阐明不同类型相图的紧邻区间 及其边界关系 2)可推导国际上已有的关于紧邻相区及 边界关系的所有实验规则和理论法则 3)可以判断并改正某些实验相图的错误 4)可在实验数据不够下粗略勾画整个相图 5)可将相图边界理论和其它热力学理论 结合起来较快的计算相图

相图边界理论最重要:相边界 相图边界理论中所定义的边界的特征为: 。R1=R时,该边界就是相边界 。R≠R时,该边界是体系边界而非相 边界,简称边界 7
7 相图边界理论最重要:相边界 相图边界理论中所定义的边界的特征为: ⚫ R 1 ’ =R1 时,该边界就是相边界 ⚫ R 1 ’≠R1时,该边界是体系边界而非相 边界,简称边界