
3)实际溶液 Hg ug(T,P)+RTLnag △,G%=∑yB4g(T,P)=-RTLnK.8 Ke(T,P) Kac=KeKx a h d d a D
1 3)实际溶液 B = B T P + RTLnaB ( , ) r Gm = B B T P = −RTLnKa ( , ) * K (T, P) a d D a A h H g G A D d G g H h d D a A h H g G a C C C C C C C C C a a a a K ( )( ) ( ) ( ) , = = Ka,C = KC K

Kax =KxKy Komn=KoK, K(T,P),K,(T,P,C) Ke(T,P,C),K(T,P,m),Kx(T,P,X) 不是平衡常数 2
2 Ka,X = KX K Ka,m = Km K K (T,P) a , K (T,P,C) K (T,P,C) C ,K (T,P,m) m ,K (T,P, X) X 不是平衡常数

6.复相反应 前面为均相反应: 浓标:X=1,P2=P9,CB=C°,mg=m 体系参加反应的物态不同(g,1,s) 复相反应 体系达多相平衡:为平衡常数K°杂 △,G8=-RTLnK°杂 3
3 6.复相反应 前面为均相反应: 浓标:XB =1, PB = P , CB = C , mB = m 体系参加反应的物态不同(g,l,s) ——复相反应 体系达多相平衡:为平衡常数 K 杂 r Gm = −RTLnK 杂

标态: 纯物质或理液:X=1 理想气体:P。=P 实际气体:fB=p 稀溶液:X=l,CB=C°,mB=m9 实际溶液:ap=1 4
4 标态: 纯物质或理液:XB =1 理想气体: PB = P 实际气体: f B = P 稀溶液:XB =1, CB = C , mB = m 实际溶液:aB =1
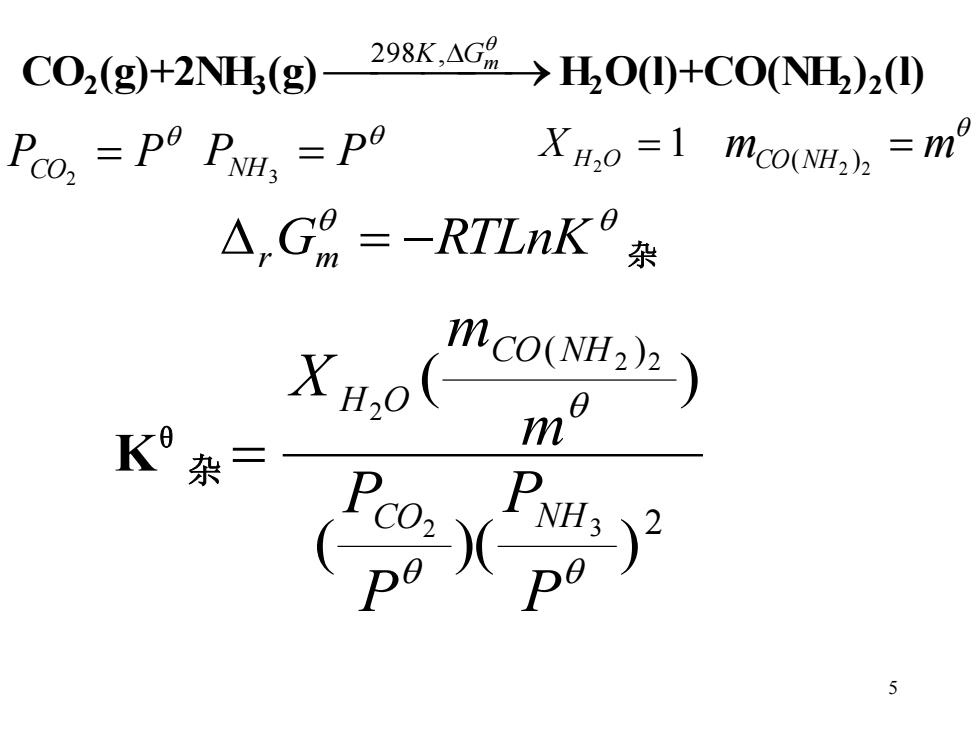
CO2(g)+2NH;(g) 298K,AG%→H,00+C0NH)20 Po,=P°PNH=P0 XHo=1 mco(NHn =m △,G9=-RTLnK杂 mco(NH22) K茶一 XH,0(m0 5
5 CO2 (g)+2NH3 (g)⎯⎯⎯ ⎯→ 298K, Gm H2 O(l)+CO(NH2 )2 (l) PCO = P 2 PNH = P 3 1 2 X H O = mCO NH = m 2 2 ( ) r Gm = −RTLnK 杂 Kθ 杂 2 ( ) ( )( ) ( ) 2 3 2 2 2 P P P P m m X CO NH CO NH H O =
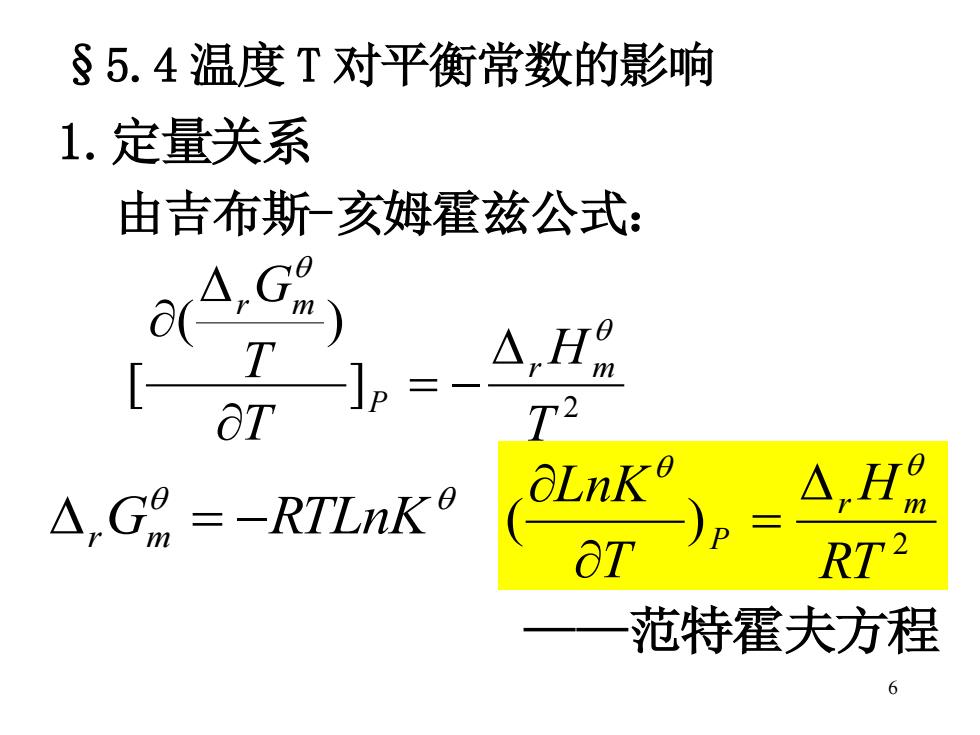
§5.4温度T对平衡常数的影响 1.定量关系 由吉布斯-亥姆霍兹公式: T △,H品 ot T2 △,G9=-RTLnK9 aLnK p △,H品 at RT2 范特霍夫方程 6
6 §5.4 温度 T 对平衡常数的影响 1.定量关系 由吉布斯-亥姆霍兹公式: 2 ] ( ) [ T H T T G r m P r m = − r Gm = −RTLnK 2 ( ) RT H T LnK r m P = ——范特霍夫方程

说明:a)标态:P。=P9XB=1CB=C9mg=m K:Ko Kx Ke Ko △,G%:△,G%A,GR△,GcA,Gm △,H:△,H品△,HR△,HR△,H △,HB与△,Hm区别在压力,理气△,H=△,Hm b)吸热△H>0,T个,K个有利正向反应 放热△H<0,T个,K↓有利逆向反应
7 说明:a)标态: PB = P XB =1 CB = C mB = m Kθ : KP KX KC Km r Gm : r Gm r Gm r Gm,C r Gm,m r Hm : r Hm r Hm ' r Hm " r Hm r Hm 与r Hm 区别在压力,理气 r Hm =r Hm b)吸热 r Hm > 0, T , K 有利正向反应 放热 r Hm < 0, T , K 有利逆向反应

2.定量计算 当AC。0)=0或A,H为常数 △,H日与T无关 Ln 成LmK=△,H8+C RT 8
8 2.定量计算 1)当 0,( ) = 0 = P r m P T H C 或 r Hm 为常数 r Hm 与 T无关 ) 1 1 ( 1 1 2 2 R T T H K K Ln r m − = 或 C RT H LnK r m + = −

LnK 9 作图 T 斜率=一 △,H品 可求△,H9 截距=C R C的物理意义:△,G=△,H-TA,S9 △,G品 RT RT R C、 4,S8 可求A,S9 R 2)当△Cp≠0,△,HR(T),LnK6=f(T)
9 T LnK 1 ~ 作图 斜率= R r Hm − 可求 r Hm 截距=C C 的物理意义: r Gm = r Hm −Tr Sm R S RT H LnK RT r Gm r m r m + = = − − R S C r m = 可求 r Sm 2)当 C 0, H (T), LnK f (T) P r m =

3.应用 1) 理想气体(低压实气) △,H品 RT2 Kg=Kx( P LnKg=LnKx+△ 1p 。. △,H aT RT2 △,H8 at RT2 10
10 3.应用 1)理想气体(低压实气) 2 ( ) RT H T LnK r m P P = = ( ) P P KP KX P P LnKP = LnKX + Ln 2 ( ) ( ) 0 RT H T LnK T LnK r m P X P P + = = 2 ( ) RT H T LnK r m P X =