
(五)速率方程的确定 确定出n,k,总结各级数反应的特点: n=0,CAo-CA=kt, 2k n =1,In- o=kt, CA tin n=2, &-=t, 1 n=3,[&高]=kt,ha 3 2k -A0
1 (五)速率方程的确定 确定出 n, k,总结各级数反应的特点:

各级反应的速率方程、动力学方程、半衰 期通式为: 速率方程: C=kC d -k 动力学方程: (n≠1) 2m-1-1 t12= (n≠1) (n-1)k Co 2
2 各级反应的速率方程、动力学方程、半衰 期通式为: 速率方程: 动力学方程:

由实验数据CAt的关系,可确定反应的级 数n和速率常数k 复杂反应:一般是先提出速率方程,然后 设计实验来验证其是否正确 简单反应n,k如何确定? 实验中得到:CA~t或CB~t变化 如何用这套数据,确定该反应的速率方 程,即n,k? 3
3 简单反应 n,k 如何确定? 由实验数据 CA~t 的关系,可确定反应的级 数 n 和速率常数 k 复杂反应:一般是先提出速率方程,然后 设计实验来验证其是否正确 实验中得到:CA ~ t 或 CB ~ t 变化 如何用这套数据,确定该反应的速率方 程,即 n,k?

1.积分法(尝试法) 对于正整数级的反应可用此法判断 将C~t数据,分别代入各动力学方程中 每组数据可求出一个k值 可确定出所求反应的级数和动力学方程 这种方法应用普遍,但不灵敏 4
4 1. 积分法(尝试法) 对于正整数级的反应可用此法判断 将 C ~ t 数据,分别代入各动力学方程中 每组数据可求出一个 k 值 可确定出所求反应的级数和动力学方程 这种方法应用普遍,但不灵敏
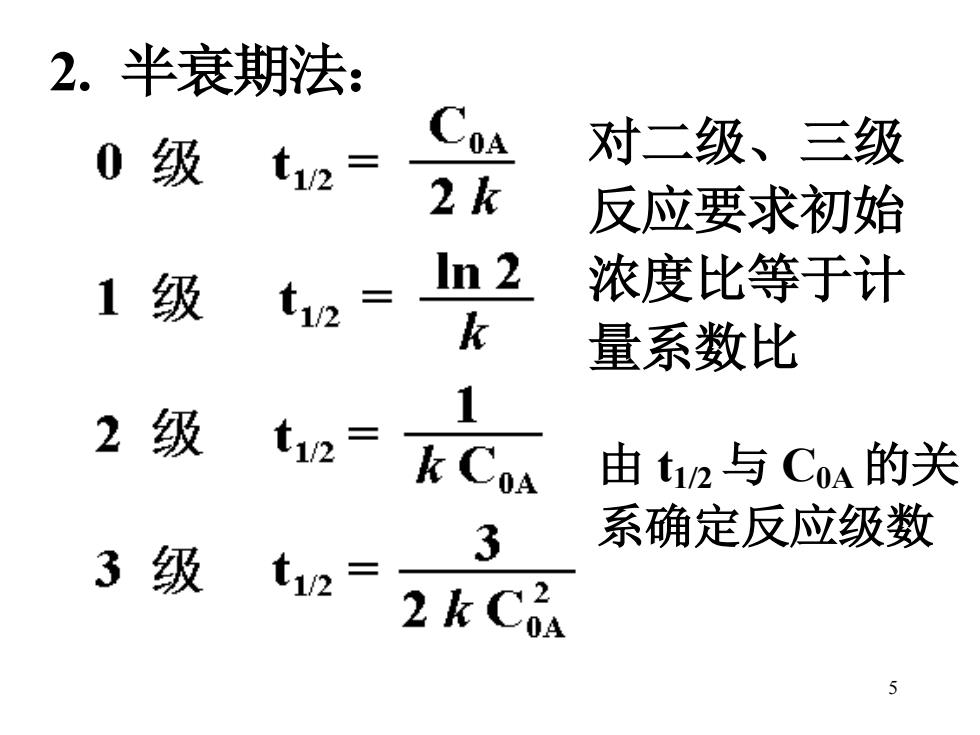
2.半衰期法: 0级 C0 对二级、三级 2k 反应要求初始 1级 In 2 t12 浓度比等于计 R 量系数比 2级 1 由t2与CoA的关 系确定反应级数 3级 3 t1v2= 5
5 2. 半衰期法: 对二级、三级 反应要求初始 浓度比等于计 量系数比 由 t1/2与 C0A的关 系确定反应级数

也可以利用t2 的通式: 2-1-1 1 t12= (n-1)kC网 (n+1) 例如:同一反应,在两个不同的初始浓度 下做实验,测得其t2 同T,P下:(CA0,tn),(CA0,t2') t2=(C C 0)n- Ln t1/2 n=1+ 2=(n-1)In C Ln- Ln 6
6 也可以利用 t1/2 的通式: 例如:同一反应,在两个不同的初始浓度 下做实验,测得其 t1/2 同 T, P 下:(C A 0, t1/2),(C A 0 ' , t1/2 ') 1 0 0 1/ 2 1/ 2 ) ' ( ' − = n A A C C t t 0 0 1/ 2 1/ 2 ' ( 1) ' A A C C n Ln t t Ln = − 0 0 1/ 2 1/ 2 ' ' 1 A A C C Ln t t Ln n = +

由两个以上的C~t数据,可确定n 此法求n,不限于t2,t3,t4都可确定 n 3.作图法: 仍为尝试法,由作图为直线确定n 若:①C心t 直线 零级 ② In C~t 直线 级 直线 二级 心t 直线 三级
7 由两个以上的 C0 ~ t 数据,可确定 n 此法求 n,不限于 t1/2,t1/3,t1/4 都可确定 n 3. 作图法: 仍为尝试法,由作图为直线确定 n

要求:数据点要多 由直线斜率求出k值,从而确定n 4.微分法: 只有一种反应物或反应物初始浓度比等于 计量系数比 速率方程: -dCa dt Ln( dC)=Lnk+ninC dCA))-InC作图 Ln(-dt 率:n,截距:lnk
8 要求:数据点要多 由直线斜率求出 k 值,从而确定 n 4. 微分法: 只有一种反应物或反应物初始浓度比等于 计量系数比 速率方程: A A Lnk nLnC dt dC Ln(− ) = + ( ) dt dC L n A − ~ LnCA 作图斜率:n , 截距:ln k
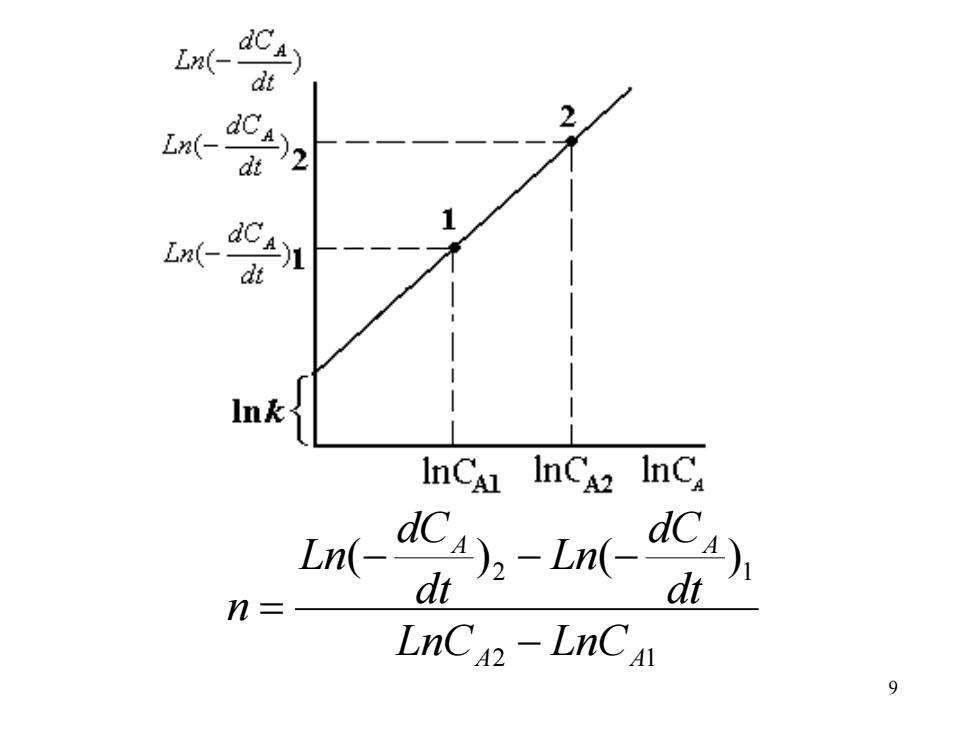
L(- dt CA) dt L(- d In 1nCA dC)-In- Ln(- dt n= LnCA2 -LnCA 9
9 2 1 2 1 ( ) ( ) A A A A LnC LnC dt dC Ln dt dC Ln n − − − − =

Ln(- (瞬时速度) 的求法: dt 采用作图法 a)测C~t数据,作C~t曲线 在各点(C1,t),(C2,),.作切线 斜率就是瞬时速度: 再利用上面的公式即可求出 10
10 ( ) dt dC Ln A − (瞬时速度)的求法: 采用作图法 a) 测 C ~ t 数据,作 C ~ t 曲线 在各点 ( C1 , t1 ) , ( C2 , t2 ) , .作切线 斜率就是瞬时速度: 1 ( ) dt dC L n A − , 2 ( ) dt dC L n A − 再利用上面的公式即可求出 n