
§6-5稳态近似与平衡态近似 是处理复杂反应动力学方程最常用的方法 可使很难求解的问题简化为一般的代数问题 ①稳态近似: B为活泼的中间产物 dCB=kCa-k,Cp dt 若2≥>k1B中间产物的浓度很小
1 §6-5 稳态近似与平衡态近似 是处理复杂反应动力学方程最常用的方法 可使很难求解的问题简化为一般的代数问题 ① 稳态近似: B 为活泼的中间产物 A B B k C k C dt dC = 1 − 2 若 k2 >> k1 B 中间产物的浓度很小

≈0 B的生成速率等于消耗速率 dt dCa=kC4-k,CB≈0 dt 这就是中间物B稳态近似 Ca= k2 中间物B: 游离原子,自由基, 活泼中间 物分子等 可以利用此稳态近似处理复杂反应
2 0 dt dCB 这就是中间物 B 稳态近似 B 的生成速率等于消耗速率 = 1 A − 2 B 0 B k C k C dt dC B CA k k C 2 1 = 中间物 B:游离原子,自由基,活泼中间 物分子等 可以利用此稳态近似处理复杂反应

稳态近似:当反应过了诱导期后,一切活 泼的反应中间物的浓度视为不随t改变 未达诱导期无效,如爆炸反应 反应中有多种中间物,则有多个这样的代数和 解出中间物浓度,以简化复杂反应动力学 例:H2+2→2HⅢ (1) 21 (2) 2I+H2 2HI 工为中间物 (3)2I ,12 dCL-kCn-k.CiCu-k;Cj=0 dt 3
3 未达诱导期无效,如爆炸反应 反应中有多种中间物,则有多个这样的代数和 解出中间物浓度,以简化复杂反应动力学 例:H2 + I2 → 2HI (1)I2 → 2I (2)2I + H2 → 2HI (3)2I → I2 k1 k2 k3 I 为中间物 稳态近似:当反应过了诱导期后,一切活 泼的反应中间物的浓度视为不随 t 改变 0 2 3 2 1 2 2 2 = I − I H − I = I k C k C C k C dt dC
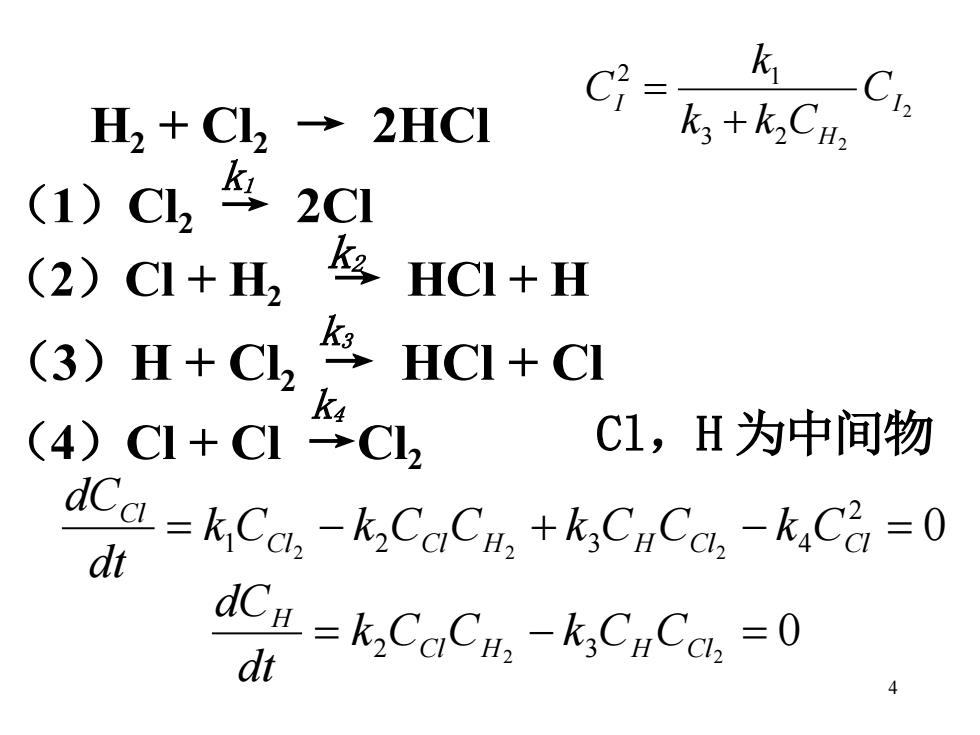
C2= k一C1, H2 +Cl2 2HCI ka+k2CHa (1)C2 2C1 (2)( CI+H2 HCI+H (3)H+C2 k9, HCI+CI k4 (4)C1+C 1→C2 C1,H为中间物 dCa-kCo.-k.CuCu.+kCyCo.-k.Ci-0 dt dCn-kCoCn-k:CnCcl=0 dt
4 2 3 2 2 2 1 I H I C k k C k C + = H2 + Cl2 → 2HCl (1)Cl2 → 2Cl (2)Cl + H2 → HCl + H (3)H + Cl2 → HCl + Cl (4)Cl + Cl →Cl2 k1 k2 k3 k4 Cl,H 为中间物0 2 = 1 Cl2 − 2 Cl H2 + 3 H Cl2 − 4 Cl = Cl k C k C C k C C k C dt dC 0 2 2 3 2 = Cl H − H Cl = H k C C k C C dt dC

平衡态近似: A空n0 k1很大时,且k2最小 2这步反应很慢,称控制步骤 用该步骤的反应速率代替整个反应的速率 其它反应相对较快,都已近似处在平衡态 这就是平衡态 5
5 ② 平衡态近似: k-1很大时,且 k2最小 k2这步反应很慢,称控制步骤 用该步骤的反应速率代替整个反应的速率 其它反应相对较快,都已近似处在平衡态 ——这就是平衡态

例:A+C→D B 机理:AK 快反应 B+C D 慢反应 由精细平衡原理: K= Ca=k K:平衡常数 Ca k2 平衡条件:r1=1,k>>2B为中间物 kC=kCR CR=MCA=KCA 6
6 例:A + C ⎯→ D 平衡条件:r1=r-1 , k-1>> k2 2 1 k k C C K A B 由精细平衡原理: = = A CB k C k 1 = −1 K:平衡常数 B CA KCA k k C = = −1 1 B 为中间物

2反应为控制步骤 y≈%=k,CCe=k kCCc=k.KC.Ce 由平衡态近似和控制步骤, 使复杂反应速率方程简化 若用稳态近似:稳态条件:k2十k1>k1 dCp.=kCx-kCg-k.CxCc=0 dt kCA kzk CaCc CB=k+kCc 7=kCiCe"ktkCe 7
7 k2反应为控制步骤 CB CC k 2 = 2 A C KCA CC C C k k k k 2 1 1 = 2 = − 由平衡态近似和控制步骤, 使复杂反应速率方程简化 若用稳态近似: = 1 A − −1 B − 2 B C = 0 B k C k C k C C dt dC C A B k k C k C C 1 2 1 + = − C A C B C k k C k k C C k C C 1 2 2 1 2 + = = − 稳态条件:k 2+ k-1 >> k1

y-kaCnCc- kzk CaCc 1+k2Cc 当k1>k2Cc时 Y= kakC Ce=kC.Ce (二级反应 k 稳态结果与平衡态结果相同 当k1<2Cc时 Y=kCa (一级反应) 8
8 C A C B C k k C k k C C k C C 1 2 2 1 2 + = = − 当 k-1 >> k2 CC时 A C A CC C C k C k k k = = −1 2 1 稳态结果与平衡态结果相同 当 k-1 << k2 CC时 CA k = 1 (二级反应) (一级反应)

第七章 基元反应的速率理论 与热力学的经典理论相比,动力学理论 发展较迟。先后形成的碰撞理论、过渡态理论都 是20世纪后建立起来的,尚有明显不足之处。 理论的共同点是:首先选定一个微观模 型,用气体分子运动论(碰撞理论)或量子力学 (过渡态理论)的方法,并经过统计平均,导出 宏观动力学中速率系数的计算公式。 由于所采用模型的局限性,使计算值与实 验值不能完全吻合,还必须引入一些校正因子, 使理论的应用受到一定的限制。 9
9 与热力学的经典理论相比,动力学理论 发展较迟。先后形成的碰撞理论、过渡态理论都 是20世纪后建立起来的,尚有明显不足之处。 理论的共同点是:首先选定一个微观模 型,用气体分子运动论(碰撞理论)或量子力学 (过渡态理论)的方法,并经过统计平均,导出 宏观动力学中速率系数的计算公式。 由于所采用模型的局限性,使计算值与实 验值不能完全吻合,还必须引入一些校正因子, 使理论的应用受到一定的限制。 第七章 基元反应的速率理论

基元反应的速率理论就是从分子基本 性质入手,研究速率常数的具体表示式 即A和活化能E的物理意义及数值 反应速率的理论很多,但都不够完善 比较成熟的速率理论有两个: 1)简单碰撞理论 在分子运动论基础上,以硬球碰撞为模 型,也叫硬球碰撞理论 2)过渡态理论 在统计热力学和量子力学基础上建立的
10 基元反应的速率理论就是从分子基本 性质入手,研究速率常数的具体表示式 即 A 和活化能 E 的物理意义及数值 反应速率的理论很多,但都不够完善 比较成熟的速率理论有两个: 1) 简单碰撞理论 在分子运动论基础上,以硬球碰撞为模 型,也叫硬球碰撞理论 2) 过渡态理论 在统计热力学和量子力学基础上建立的