
第五章相平衡热力学 §5-1相变和相变熵 系统中物理性质和化学性质完全相同的部分称为相,物质 从一个相流动到另一个相的过程,称为相变化,简称相变。 相变化(包括气化、冷凝、熔化、凝固、升华、凝华以 及晶型转化等) 1相变焓 通常谈到相变化都是指定温、定压,W=0时的变化过 程, 因此相变过程的热艺是想变榜,即
第五章 相平衡热力学 §5-1 相变和相变熵 系统中物理性质和化学性质完全相同的部分称为 相,物质 从一个相流动到另一个相的过程,称为相变化,简称相变 。 相变化 (包括气化 、冷凝 、熔化 、凝固 、升华 、凝华 以 及晶型转化 等 ) 1 相变焓 通常谈到相变化都是指定温、定压,W‘ =0 时的变化过 程, 因此相变过程的热就是相变焓,即 Q p H β = ∆ α

相变焓:蒸发烙:AvapHm,熔化烙:△usHm,升华焙:△ubHm 晶型转变焓:△rHm 为了计算各种相变过程的热效应,需从化学、化工手册 上查找称为摩尔相变焓的基础实验数据。摩尔相变焓指1mol 纯物质于恒定温度及该温度的平衡压力下发生相变时相应的 焓变,以符号△。BHm(T)表示,单位:kmol。所以, 摩尔蒸发焓ApHm心[Hng-Hm)=A月Hm (5-1-1) 摩尔溶化焓AsHm世Hn)-Hm)=AHm (5-1-2) 摩尔升华焓4 u HH(g)-Hm=AHm (5-1-3) 摩尔转变焓4HmHm(Cr,2)-Hm(Cr,)=AHm (5-1-4) 摩尔冷凝焓为-△aHnm,摩尔结晶焓为-△Hm,摩尔凝华焓 为-△bHm
(5-1-1) 相变焓: 蒸发焓: ∆vapH m,熔化焓: ∆fusH m, 升华焓: ∆subH m, 晶型转变焓: ∆trsH m 为了计算各种相变过程的热效应,需从化学、化工手册 上查找称为摩尔相变焓的基础实验数据。摩尔相变焓指1mol 纯物质于恒定温度及该温度的平衡压力下发生相变时相应的 焓变,以符号ΔαβHm( T )表示,单位:kJ·mol-1。所以, m g m m l def ∆vapHm H (g) − H (l) =∆ H m l m m s def ∆ fusHm H (l) − H (s) =∆ H m g m m s def ∆subHm H (g) − H (s) =∆ H m Cr m m Cr def ∆trsHm H Cr H Cr ∆ H,2,1 ( ,2) − ( ,1) = 摩尔蒸发焓 (5-1-2) (5-1-3) (5-1-4) 摩尔溶化焓 摩尔升华焓 摩尔转变焓 摩尔冷凝焓为-ΔvapHm,摩尔结晶焓为-ΔfusHm,摩尔凝华焓 为-ΔsubHm

在恒温、恒压、非体积功为零的条件下,物质的量为n的某 物质的相变焓可用下式计算 △相变H=n△相变Hm=p (5-1-5) 由于相变过程是在恒压、不作非体积功条件下进行,所以此 相变过程的焓差就等于此过程系统与环境交换的热Q,· 例5-1-1在101.325kPa下,汞的沸点为630K,气化时吸热 291.6 kJ-kg-1,汞气化过程为Hg(1)=Hg(g) 求1.00mol汞在此过程的W、Q、△U及△H。设汞蒸气在此温度 下为理想气体,液体汞的体积可以忽略。(M200.6gmo1) 解:△H=n△aIH=(1.00×291×200.6×103)k=58.5kJ W=-p"g')Fpg-nRT-1.00×8.3145×630kJ=-5.24kJ Q,=△H=58.5kJ △U=2,+W=(58.5-5.24)kJ=53.3kJ
在恒温、恒压、非体积功为零的条件下,物质的量为 n的某 物质 的相变焓可用下式计算 Δ相变H = n Δ相变 Hm = Qp (5-1-5 ) 由于相变过程是在恒压、不作非体积功条件下进行,所以此 相变过程的焓差就等于此过程系统与环境交换的热 Qp 。 例5-1-1 在101.325kPa下,汞的沸点为630K,气化时吸热 291.6kJ·kg-1,汞气化过程为 Hg(1) = Hg(g) 求1.00mol汞在此过程的 W、 Q、Δ U及Δ H。设汞蒸气在此温度 下为理想气体,液体汞的体积可以忽略。( MHg=200.6g·mol-1 ) 解:ΔH = n Δ vapH = (1.00 ×291 ×200.6 ×10-3)kJ = 58.5kJ W= -p ( Vg - V1)= -pVg= -nRT= -1.00 ×8.3145 ×630kJ = -5.24kJ Q p = ΔH = 58.5kJ ΔU = Qp +W = (58.5-5.24)kJ = 53.3kJ

2、相变焓与温度的关系 由于物质的焓是温度与压力的函数,故相变焓应为温度与压力 的函数。但相变焓是指某温度T及该温度对应的平衡压力下物 质发生相变时的焓差,而与温度对应的平衡压力又是温度的函 数,所以摩尔相变焓可归结为温度的函数。一般手册上大多只 列出某个温度、压力下的摩尔相变焓数据,这样,就必须知道 如何由T、p1下的摩尔相变焓数值去求任意温度T,及压力pP2下摩 尔相变焓数值,下面举例说明如何计算。 若有1mol物质B在p1、T,条件下由液相转变为气相,其摩 尔气化焓为△vap Hm(Ti),求在T2p2条件下的△vapHm(T)。求解 状态函数增量问题,必须利用状态函数增量只与始末态有关而 与途径无关的特点,为此可设计如下的过程:
2、相变焓与温度的关系 由于物质的焓是温度与压力的函数,故相变焓应为温度与压力 的函数。但相变焓是指某温度 T 及该温度对应的平衡压力下物 质发生相变时的焓差,而与温度对应的平衡压力又是温度的函 数,所以摩尔相变焓可归结为温度的函数。一般手册上大多只 列出某个温度、压力下的摩尔相变焓数据,这样,就必须知道 如何由T1、p1下的摩尔相变焓数值去求任意温度T2及压力p2下摩 尔相变焓数值,下面举例说明如何计算。 若有1mol物质 B 在 p1、T1 条件下由液相转变为气相,其摩 尔气化焓为ΔvapHm(T1),求在T2、p2条件下的ΔvapHm(T2)。求解 状态函数增量问题,必须利用状态函数增量只与始末态有关而 与途径无关的特点,为此可设计如下的过程:
B(1)n=1mol △Hnm(T2) B(g)n=1mol T2,p2 T2,p2 △H1 △H4 B(1)n=1mol B(g)n=1mol T1,p2 T1,p2 △H2 △H3 B(1)n=1mol B(g)n=1mol TP △Hm(T) T p 则 △vapHm(T2)F△H+△H2+△pHm(Ti)+△H3+△H4 △H表示在恒温下压力从p2变至p时液体的焓变,压差不大 时可忽略,即△H,≈O:△H为B蒸气在恒温变压时的焓差, 若该蒸气视为理想气体,则△H,=0。这样
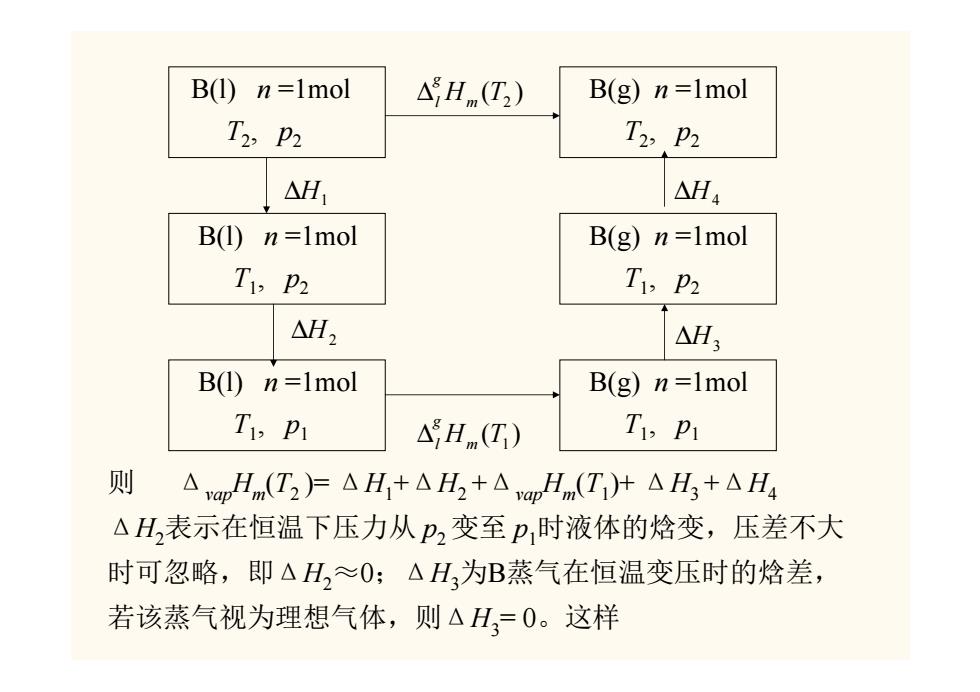
B(l) n =1mol T2, p2 B(l) n =1mol T1, p2 B(l) n =1mol T1, p1 B(g) n =1mol T2, p2 B(g) n =1mol T1, p2 B(g) n =1mol T1, p1 ( ) Hm T2 g ∆l ( ) Hm T1 g ∆l ∆H1 ∆H3 ∆H2 ∆H4 则 ΔvapHm(T2 )= ΔH1+ΔH2 +ΔvapHm(T1)+ ΔH3 +ΔH4 ΔH2表示在恒温下压力从 p2 变至 p1时液体的焓变,压差不大 时可忽略,即ΔH2≈0;ΔH3为B蒸气在恒温变压时的焓差, 若该蒸气视为理想气体,则ΔH3= 0。这样

△apHn(T)=△aHm(Ti)+△H1+△H4 而: H=∫6Cpn④dnAH,-jC,n(gdr .AwH.G)-AwH.(7)+"Cpm(NT+C(gdT △mHn(G)=ApH(G)+∫[Cn(g)-C(]d77 上式表明,若知道△aIHn(T1)及Cnm(I)和Cnm(g)的数值,则 不难求得另一温度T2下B的摩尔蒸发焓△pHm(T2)。上式还表明, △aHm随温度而变的原因在于Cm(g)与Cm(I)不等
Δ vapHm(T2) =ΔvapHm(T1) +ΔH1+ΔH4 而: , ∫ ∆ = 12 1 , (1) TT p m H C dT ∫ ∆ = 21 4 , ( )d TT H Cp m g T H T H T C T C g T T T p m T T vap m( ) vap m( ) p m(1)d ( )d 21 12 ∴ ∆ 2 =∆ 1 +∫ , +∫ , [ ] ∫ ∆ = ∆ + − 21 2 1 , , ( ) ( ) ( ) (1) d TT vapHm T vapHm T Cp m g Cp m T (5-1-6) 上式表明,若知道ΔvapHm(T1)及Cp,m(1)和Cp,m(g)的数值,则 不难求得另一温度T2下B的摩尔蒸发焓ΔvapHm(T2)。上式还表明, Δ vapHm随温度而变的原因在于Cp,m(g)与Cp,m(1)不等。 (5-1-6)

例5-1-2已知水在100℃、101.325kPa下其摩尔蒸发焓 △apHm(100C)=40.63 kJ.mol-1,水与水蒸气的平均摩尔定压 热容分别为Cm(1)=76.56 Jmol-1.K1,Cmg=34.56 Jmol-1.K 设水蒸气为理想气体,试求水在142.9℃及其平衡压力下的 摩尔蒸发焓△aHm(142.9℃)。 费乳大添q+因-C0如 =AaH(1OOC)+Cpm(g)-Cpm(I(T-T) △mHm(142.9°C)=40.63+(34.56-76.56×103×(416.1-373.2) =38.83kJmoΓ
例5-1-2 已知水在100℃、101.325kPa下其摩尔蒸发焓 Δ vapHm(100℃)=40.63kJ·mol-1,水与水蒸气的平均摩尔定压 热容分别为 Cp,m(1)=76.56J·mol-1·K-1 , Cp,m(g)=34.56J·mol-1·K- 1 。 设水蒸气为理想气体,试求水在142.9℃及其平衡压力下的 摩尔蒸发焓ΔvapHm(142.9℃)。 解:根据相变热与温度的关系: [ ] ∫ ∆ =∆ + − 416.1 373.2 , , vapHm(142.9 C) vapHm(100C) Cp m(g) Cp m(1) dT o o (100 ) [ ] ( ) (1) ( ) =∆vapHm C + Cp,m g −Cp,m T2 −T1 o 1 3 38.83kJ mol (142.9 ) 40.63 (34.56 76.56 10 (416.1 373.2) − − = ⋅ ∆vapHm C = + − × × − o

3.相变化过程熵变的计算 (1)可逆相过程相变熵 所谓可逆相变是指在无限接近相平衡条件下进行的相变 化。 什么是无限接近相平衡的条件呢?例如,373.15K水的饱和蒸 气压为101.325kPa,所以373.15K、101.325kPa的水与 373.15K、 101.325kPa的水蒸气组成的系统就是处于相平衡状态的系统。 若将蒸气的压力减少了dp,则水与水蒸气的平衡被破坏,于是 水就要蒸发。此时水是在无限接近平衡条件下进行相变的,故 为可逆相变。 任何纯物质的可逆相变均具有恒温、恒压的特点,所以恒 温恒压和无限接近相平衡条件下的相变过程的热(即可逆热) 就是前面介绍的相变焓。根据熵变的定义式,对于恒温恒压的
3. 相变化过程熵变的计算 (1)可逆相过程相变熵 所谓可逆相变是指在无限接近相平衡条件下进行的相变 化。 什么是无限接近相平衡的条件呢?例如,373.15K水的饱和蒸 气压为101.325kPa,所以373.15K、101.325kPa的水与 373.15K、 101.325kPa的水蒸气组成的系统就是处于相平衡状态的系统。 若将蒸气的压力减少了dp,则水与水蒸气的平衡被破坏,于是 水就要蒸发。此时水是在无限接近平衡条件下进行相变的,故 为可逆相变。 任何纯物质的可逆相变均具有恒温、恒压的特点,所以恒 温恒压和无限接近相平衡条件下的相变过程的热(即可逆热) 就是前面介绍的相变焓。根据熵变的定义式,对于恒温恒压的 可逆相变 相变熵为

△相变S= △相变H (5-1-7) T 摩尔熔化熵△加s世Sn(0-Sn(s)=A,Sn (5-1-8) 摩尔蒸发痛△apSn世Sm(g)-Sn()=△Sn (5-1-9) def 摩尔升华熵△bS二Sm(g)-Sm(S)=△Sm (5-1-10) 摩尔转变熵 △(C,2)-Snm(C,)=Ag3Sm (5-1-11) 在讨论相变时,总会提到相变温度。例如汽化时的沸 点, 沸点是指液体的饱和蒸气压与环境压力相等时的沸腾温度。如 果环境压力为101.325kPa,液体的沸腾温度称为正常沸点或标 准沸点。在正常相变点发生相变时,都有是可逆的
T H S 相变 相变 ∆ ∆ = (5-1-7) m g m m l def ∆vap S m S (g) − S (l) = ∆ S m l m m s def fus ∆ S S (l) − S (s) = ∆ S m g m m s def ∆sub S S (g) − S (s) = ∆ S m Cr m m Cr def trsSm S Cr S Cr S,2,1 ∆ ( ,2) − ( ,1) = ∆ 摩尔熔化熵 摩尔蒸发熵 摩尔升华熵 摩尔转变熵 (5-1-8) (5-1-9) (5-1-10) (5-1-11) 在讨论相变时,总会提到相变温度。例如汽化时的沸 点, 沸点是指液体的饱和蒸气压与环境压力相等时的沸腾温度。如 果环境压力为101.325kPa,液体的沸腾温度称为正常沸点或标 准沸点。 在正常相变点发生相变时,都有是可逆的

例5-1-3计算1mol甲苯在正常沸点110℃下完全蒸发为蒸气的过 程的相变熵△相变S。己知△wapHm(甲苯)=33.5 kJ-mol 解:在101.325kPa、110℃的液体甲苯在恒T、p下相变为 110℃、 101.325kPa的甲蟻蒸先。这是在正常相变点发生可逆相 变, A相变二 T 因此 n△Hm_1×33500 (J.K) T 383.15 =87.43JK-
例5-1-3 计算1mol甲苯在正常沸点110℃下完全蒸发为蒸气的过 程的相变熵Δ相变S。已知ΔvapHm(甲苯) = 33.5kJ·mol- 1 。 解:在101.325kPa、110℃的液体甲苯在恒T、p下相变为 110℃、 101.325kPa的甲苯蒸气。这是在正常相变点发生可逆相 变, 因此 T H S 相变 相变 ∆ ∆ = (J.K ) 383 .15 1× 33500 −1 = ∆ = T n H m gl 1 87.43J.K − =