
第四章 化学动力学
第四章 化 学 动 力 学

§1化学动力学的任务与概况 化学动力学的任务 化学热力学研究(战略问题一可能性): 化学反应自动进行的方向、限度及平衡条件。 化学动力学研究(战术问题一可行性): 化学反应进行的速率、机理和影响速率的因素。 H2(g)+0.502(g)==H20) A,GA(298.15K)=-237.19kJ.mol 2NO2(g)===N2O4(g) △,G92(298.15K)=-5.39Jmol
§1 化学动力学的任务与概况 一、化学动力学的任务 化学热力学研究(战略问题——可能性): 化学反应自动进行的方向、限度及平衡条件。 化学动力学研究(战术问题——可行性) : 化学反应进行的速率、机理和影响速率的因素。 H2 (g) + 0.5O2 (g) ==== H2O(l) 1 r m,1 (298.15K) 237.19kJ mol − G = − 2NO2 (g) ==== N2O4 (g) 1 r m,2 (298.15K) 5.39kJ mol − G = −

当A,G。0时,动力学研究无意义。 热力学上得到肯定的反应,通过动力学研究, 寻找提高反应速率的途径。 二、化学动力学的发展概况 质量作用定律一阿仑尼鸟斯公式 碰撞 理论一过渡状态理论 一分子反应动态学 1宏观反应动力学:从宏观的角度研究反应的机 理和动力学行为,各种宏观因素对速率的影响
当 r GT , p <0时,动力学研究有意义。 当 r GT , p >0时,动力学研究无意义。 热力学上得到肯定的反应,通过动力学研究, 寻找提高反应速率的途径。 二、化学动力学的发展概况 质量作用定律 阿仑尼乌斯公式 碰撞 理论 过渡状态理论 分子反应动态学 1.宏观反应动力学:从宏观的角度研究反应的机 理和动力学行为,各种宏观因素对速率的影响

2.元反应动力学:借助统计力学的方法,从微观 分子反应的动力学行为特征出发,研究宏观元反 应动力学。 3.分子反应动力学:借助量子力学的方法,通过 对分子束散射技术和远红外化学冷光等现象的研 究,探究分子经碰撞发生化学反应的动力学行为 及能量传递和变化等问题。 速率涉及时间:年一飞秒 飞秒化学 浓度涉及空间:线性 分形 非线性
2. 元反应动力学:借助统计力学的方法,从微观 分子反应的动力学行为特征出发,研究宏观元反 应动力学。 3. 分子反应动力学:借助量子力学的方法,通过 对分子束散射技术和远红外化学冷光等现象的研 究,探究分子经碰撞发生化学反应的动力学行为 及能量传递和变化等问题。 速率涉及时间: 年 飞秒 飞秒化学 浓度涉及空间:线性 分形 非线性
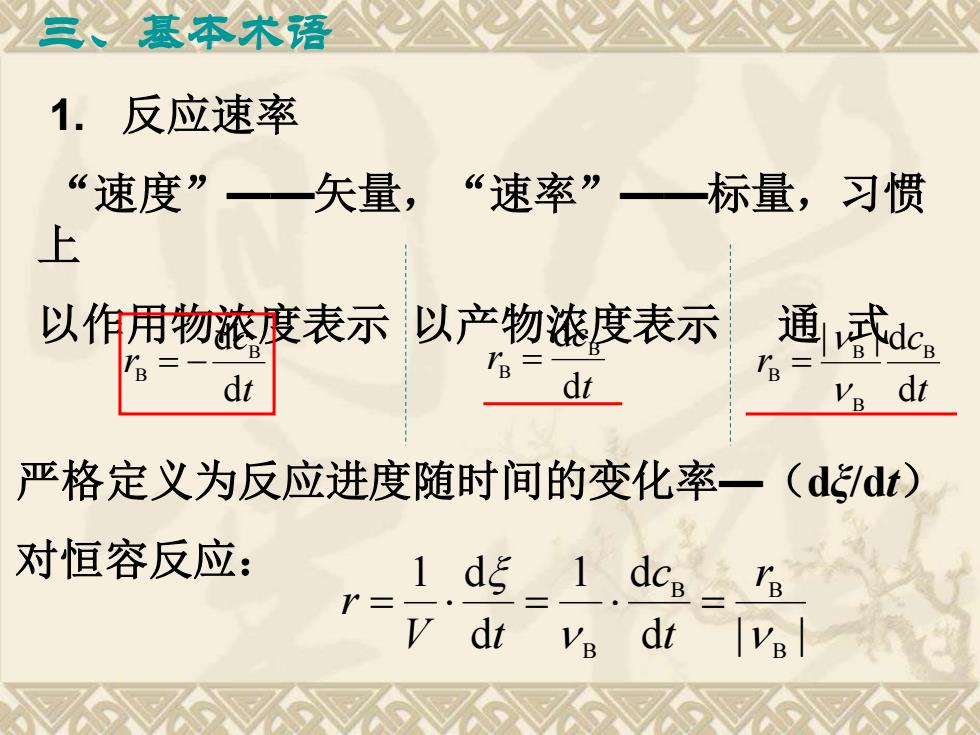
基本术语 1.反应速率 “速度”一矢量,“速率”一标量,习惯 上 以作用物浓渡表示以产物浓度表示 通武dc。 B= dt TB= dt R dr 严格定义为反应进度随时间的变化率一(ddt) 对恒容反应: 1dξ_1dc Y= v dt Ve dt VB
三、基本术语 1. 反应速率 “速度”——矢量,“速率”——标量,习惯 上 以作用物浓度表示 以产物浓度表示 通 式 t c r d d B B = − t c r d d B B = t c r d | | d B B B B = 严格定义为反应进度随时间的变化率—(dξ/dt) 对恒容反应: d | | 1 d d 1 d B B B B r t c V t r = = =

对反应aA+FxX+yY而言: r=_ 1.de=1.dc=1.des =1.dc dt f dt dt y dt 或:====5 >0 2. 元反应 构成化学反应的最基本反应步骤称为元反应; 即:由作用物粒子直接反应生成产物粒子的反应。 两个以上的元反应构成的总(包)反应称为非元反 应或复杂反应
对反应 aA + fF →xX + yY而言: t c t y c t x c t f c a r d 1 d d 1 d d 1 d d 1 d A F X Y = − = − = = 或: y r x r f r a r r A F X Y = = = = >0 2. 元反应 构成化学反应的最基本反应步骤称为元反应; 即:由作用物粒子直接反应生成产物粒子的反应。 两个以上的元反应构成的总(包)反应称为非元反 应或复杂反应

总(包)反应:H2+2→2HⅢ ①IL2→2I ②2I→2 ③HL2+2I→2HI 3.反应机理(历程) 一个总包化学反应中所包含的元反应按序排 列就构成该总包化学反应的机理(历程)。 4.反应速率方程 r=f(CA,CB,CNyT) 一般指定温度,则 r=∫(CA,CB,CN)一反应速率方程
3. 反应机理(历程) 一个总包化学反应中所包含的元反应按序排 列就构成该总包化学反应的机理(历程)。 4. 反应速率方程 r = f(cA, cB, . .,cN,T) 一般指定温度,则 r = f(cA, cB, . .,cN)—— 反应速率方程 总(包)反应: H2+ I2 →2HI ①I2 → 2I ②2I → I2 ③H2 + 2I → 2HI

(1)质量作用定律 元反应速率方程 在一定温度下,r∝(C作用物)”, aA+fP→xX+yY 1 n=kackcr dt A=一 dt dc r= = -krcacp a f X y dt dcx=kc只c k k= kA」 kx k / dt a f X y dcy k:反应速率常数 dt k:反应速率常数
(1)质量作用定律——元反应速率方程 在一定温度下, r ∝ (c作用物) n , aA + fF → xX + yY a f k c c t c r A A F A A d d = − = a f k c c t c r F A F F F d d = − = a f k c c t c r X A F X X d d = = a f k c c t c r Y A F Y Y d d = = a f kc c t c r A F B B d 1 d = = y r x r f r a r r A F X Y = = = = y k x k f k a k k A F X Y = = = = k:反应速率常数 kB :反应速率常数
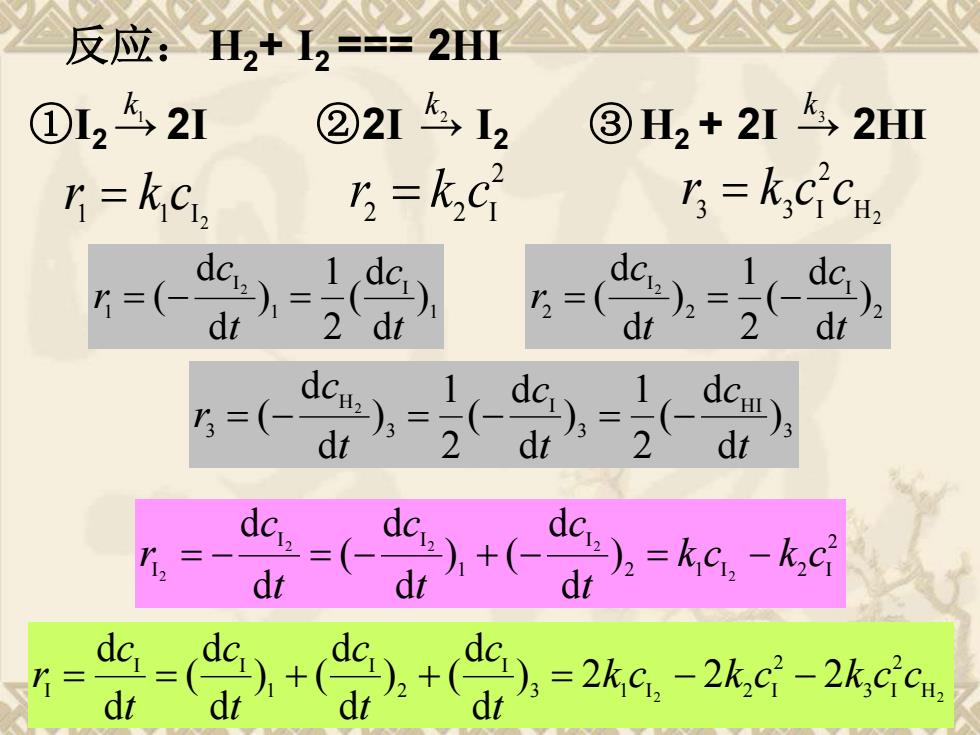
反应:H2+12==2HⅢ ①L242I ②2I2 ③H2+2I42HⅢ r=kci, n=kc =k; ( dc) dt 当-告当=22-
反应: H2+ I2 === 2HI ①I2 → 2I ②2I → I2 ③H2 + 2I → 2HI 2 1 1 I r = k c 2 2 2 I r = k c 1 k 2 k 3 k H2 2 3 3 I r = k c c 1 I 1 I 1 ) d d ( 2 1 ) d d ( 2 t c t c r = − = 2 I 2 I 2 ) d d ( 2 1 ) d d ( 2 t c t c r = = − 3 H I 3 I 3 H 3 ) d d ( 2 1 ) d d ( 2 1 ) d d ( 2 t c t c t c r = − = − = − 2 2 1 I 2 I I 1 I I I 2 2 2 2 2 ) d d ) ( d d ( d d k c k c t c t c t c r = − = − + − = − 2 H2 2 3 I 2 3 1 I 2 I I 2 I 1 I I I ) 2 2 2 d d ) ( d d ) ( d d ( d d k c k c k c c t c t c t c t c r = = + + = − −

(2)复杂反应速率方程 aA+fF→xX+yY ▲幂函数形式: r-1.dc=kecc<c dt 许多反应y=0,6=0 反应速率只与 则:r=1 1 dce kcace 作用物浓度有关 VB dt 非幂函数形式: kckCP CxCY r= V dt 1+k'ccgc以cg 如式(7-6)
(2)复杂反应速率方程 aA + fF → xX + yY ▲ 幂函数形式: A F X Y B B d 1 d kc c c c t c r = = ▲ 非幂函数形式: ' Y ' X ' F ' A B A F X Y B d 1 ' 1 d k c c c c kc c c c t c r + = = 许多反应 = 0, = 0 则: A F B B d 1 d kc c t c r = = 反应速率只与 作用物浓度有关 如式(7-6)