
§3.热化学 化学反应过程的△U和△H 一、化学反应热效应 1.热效应: 无有效功时,化学反应的等温反应过程热(Q) 。 化学反应过程是一个复杂过程,伴有状态函数 变化△U、△H,也有过程函数W、O等。 无有效功的恒容过程:Q=△U,记为△U 无有效功的恒容过程:9,=△H,记为△H 将过程函数与体系容量性质(状态函数变化量) 联系在一起
§3.热化学——化学反应过程的△U和△H 一、化学反应热效应 1.热效应: 无有效功时,化学反应的等温反应过程热(Q) 。 化学反应过程是一个复杂过程,伴有状态函数 变化△U、△H,也有过程函数W、Q等。 无有效功的恒容过程:QV = △U,记为△rU 无有效功的恒容过程:Qp = △H,记为△rH 将过程函数与体系容量性质(状态函数变化量) 联系在一起

影响热效应的因素有: (1)反应的本性;(3)反应物的存在形态; (2)反应的温度;(4)反应方程式的写法。 2.热化学方程式 反应进度为1摩尔(-1mol)时的反应热效应 称为摩尔反应热效应,记为△Hm、△,Um
影响热效应的因素有: (1)反应的本性; (3)反应物的存在形态; (2)反应的温度; (4)反应方程式的写法。 2. 热化学方程式 反应进度为1摩尔(ξ=1mol)时的反应热效应 称为摩尔反应热效应,记为△rHm、△rUm

要求:(1)完整的化学计量方程式;(2)注明 反应的温度和压强(或体积),如:△H(298K) (3)注明反应体系中各物质的存在形态,包括 S,1,g,晶型等。注意上、下标!! C(石墨)+02(g)=C02(g) △,H(298K)=-393.51 kJ.mol-
C(石墨) + O2(g) CO2(g) 1 r m (298K) 393.51kJ mol − H = − 要求:(1)完整的化学计量方程式;(2)注明 反应的温度和压强(或体积),如: (3)注明反应体系中各物质的存在形态,包括 s,l,g,晶型等。注意上、下标!! (298K) r m H
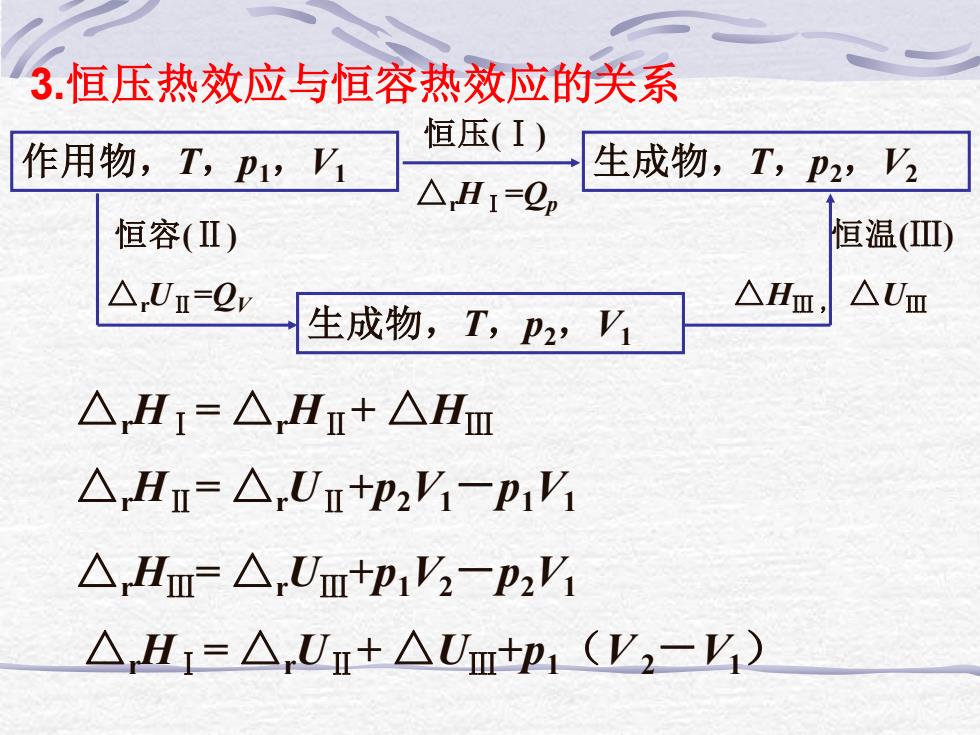
3.恒压热效应与恒容热效应的关系 恒压(I) 作用物,T,P1,V 生成物,T,p2,V △H1=2p 恒容(Ⅱ) 恒温(Ⅲ) △Um=2w 生成物,T,p2,V1 △Hm, △Um △H1=△Hn+△Hm △H=△Um+P2V-p1V △Hm=△Um+p1V-p2'i △Hr=△Ur+△U+p1(V2-Y)
3.恒压热效应与恒容热效应的关系 作用物,T,p1,V1 生成物,T,p2,V2 恒压(Ⅰ) △rHⅠ=Qp 生成物,T,p2,V1 恒容(Ⅱ) △rUⅡ=QV 恒温(Ⅲ) △HⅢ , △UⅢ △rHⅠ= △rHⅡ+ △HⅢ △rHⅡ= △rUⅡ+p2V1-p1V1 △rHⅢ= △rUⅢ+p1V2-p2V1 △rHⅠ= △rUⅡ+ △UⅢ+p1(V 2-V1)

产物是理想气体或凝聚态物质都有:△Um=0 则:△H=△Um+p1(V2-V) △H1是恒压热效应,△,U1是恒容热效应 即:恒压热效应=恒容热效应+p△V △H=△U+p△V (1)对凝聚态反应体系:△V0 则:恒压热效应≈恒容热效应, △H≈△U或△Hm≈△Um
产物是理想气体或凝聚态物质都有:△rUⅢ=0 则:△rHⅠ= △rUⅡ+ p1(V 2-V1) △rHⅠ是恒压热效应, △rUⅡ是恒容热效应 即:恒压热效应 = 恒容热效应 +p △V △rH = △rU +p △V (1)对凝聚态反应体系:△V≈0 则:恒压热效应≈恒容热效应, △rH ≈ △rU 或 △rHm ≈ △rUm
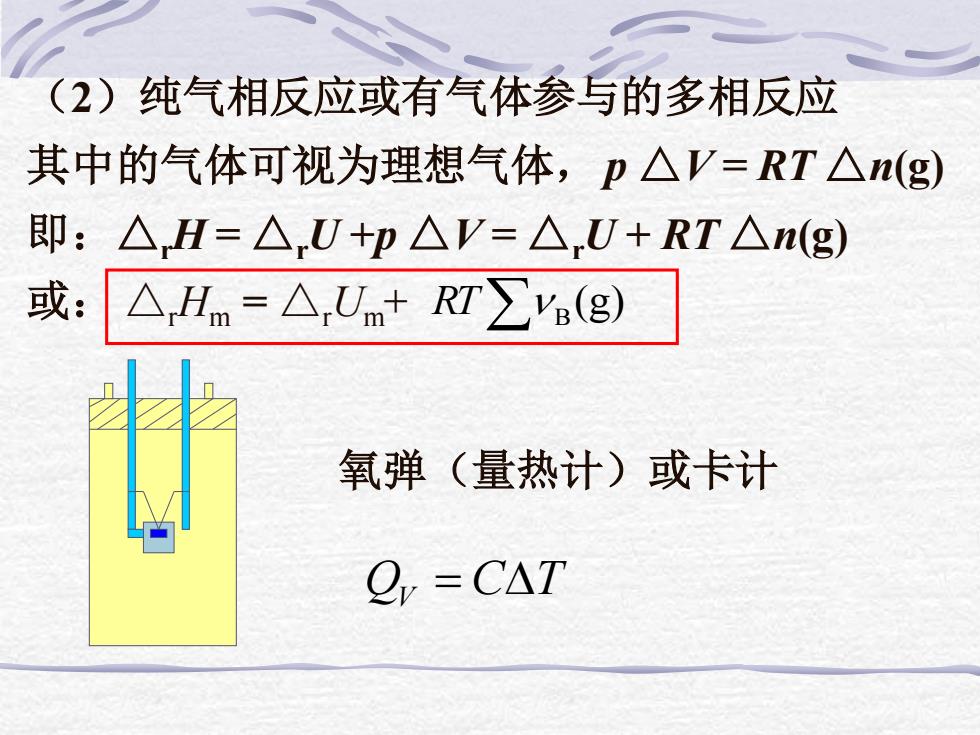
(2)纯气相反应或有气体参与的多相反应 其中的气体可视为理想气体,p△V=RT△n(g) 即:△H=△U+p△V=△U+RT△n(g) 或:△Hm=△,Unm+RT∑(g) 氧弹(量热计)或卡计 =CAT
(2)纯气相反应或有气体参与的多相反应 其中的气体可视为理想气体,p △V = RT △n(g) 即:△rH = △rU +p △V = △rU + RT △n(g) 或: △rHm = △rUm + (g) RT B QV = CT 氧弹(量热计)或卡计
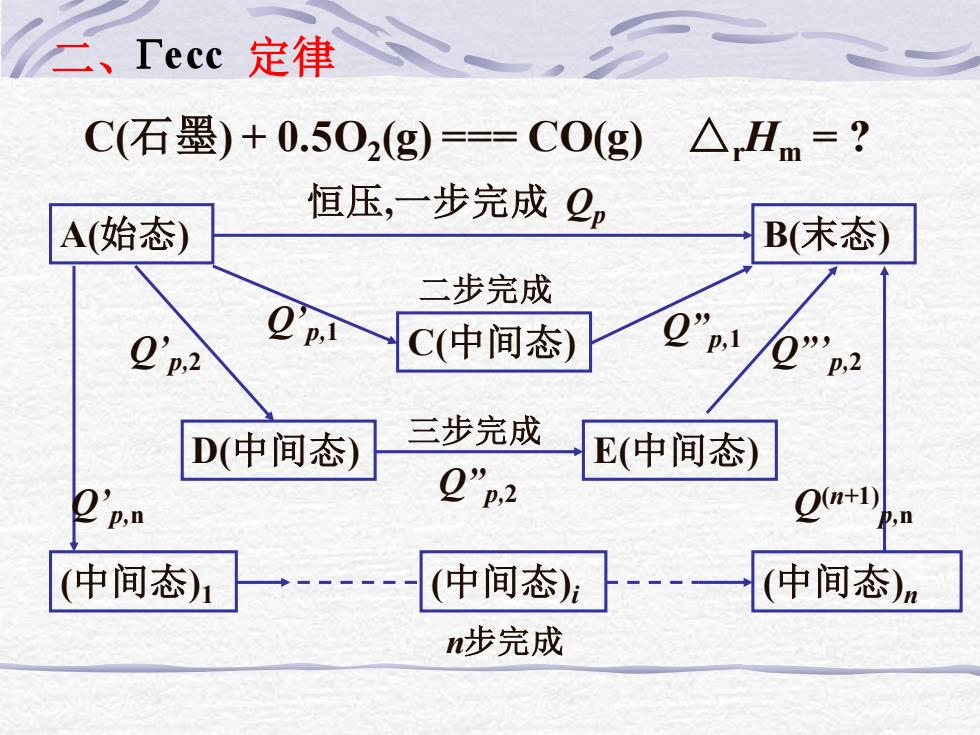
二、Tecc定律 C(石墨)+0.502(g)==C0(g)△Hm=? 恒压,一步完成2p A(始态) B(末态 二步完成 0'p2 C(中间态) Q p,1 p,2 D(中间态) 三步完成 E(中间态) 2"p2 p,n O(n+1) (中间态)1 (中间态) (中间态)n n步完成
A(始态) B(末态) 恒压,一步完成 Qp C(中间态) Q’p,1 Q”p,1 D(中间态) E(中间态) 二步完成 Q’p,2 Q”p,2 Q”’p,2 三步完成 (中间态)1 (中间态)i (中间态)n n步完成 Q’p,n Q(n+1) p,n 二、 定律 C(石墨) + 0.5O2 (g) === CO(g) △rHm = ? ecc

按盖斯定律有: 2p='1+”l =0'p2+2p2+0”"n2 ='pn+2”pn+ P,n 即,热化学方程可以进行代数式一样的加减运算, 故,热效应也可以进行对应的运算。 在无有效功的条件下,△H=2,因此,热效应 的代数和运算就是状态函数的代数和运算
按盖斯定律有: Qp = Q’p,1 + Q”p,1 = Q’p,2 + Q”p,2 + Q”’p,2 = Q’p,n + Q”p,n + + Q(n+1) p,n 即,热化学方程可以进行代数式一样的加减运算, 故,热效应也可以进行对应的运算。 在无有效功的条件下,△rH = Qp,因此,热效应 的代数和运算就是状态函数的代数和运算

C(石墨)+0,(g)==C0,g △,Hmw 可测 -)C0(g)+0.502(g)=C02(g)△Hm2可测 C(石墨)+0.502(g)==C0(g) △Hm=△Hmw-△Hm2 (1)涉及的各反应必须有完整的热化学方程; (2)各反应的条件完全相同; (3)无非体积功存在。 盖斯定律的方法可推广到化学反应的其他状态 函数的计算
C(石墨) + O2 (g) === CO2 (g) △rHm(1) 可测 -) CO (g) + 0.5O2 (g) === CO2 (g) △rHm(2) 可测 C(石墨) + 0.5O2(g) === CO(g) △rHm = △rHm(1) - △rHm(2) (1)涉及的各反应必须有完整的热化学方程; (2)各反应的条件完全相同; (3)无非体积功存在。 盖斯定律的方法可推广到化学反应的其他状态 函数的计算

三、热化学数据的建立及应用 1.标准生成热 ▲定义:在指定条件(p,T)下,由稳定单质 元素反应生成1mol化合物时的热效应。记为: △HO(B,T) 其中B代表所生成的化合物。 特别提醒: ()单质:非单质间的反应不能构成“生成反应”。 C0g)+0.502(g)===C02(g)
特别提醒: (1) 单质:非单质间的反应不能构成“生成反应”。 CO(g) + 0.5O2 (g) ==== CO2 (g) 三、热化学数据的建立及应用 1.标准生成热 ▲定义:在指定条件(p Θ ,T)下,由稳定单质 元素反应生成1mol化合物时的热效应。记为: (B, ) f Hm T 其中B代表所生成的化合物