
第三章原子结构 §3-1原子核外电子运动状态 电子围绕原子核高速运转, 从最简单的原子氢光谱开始研究
第三章 原子结构 §3-1 原子核外电子运动状态 电子围绕原子核高速运转, 从最简单的原子氢光谱开始研究

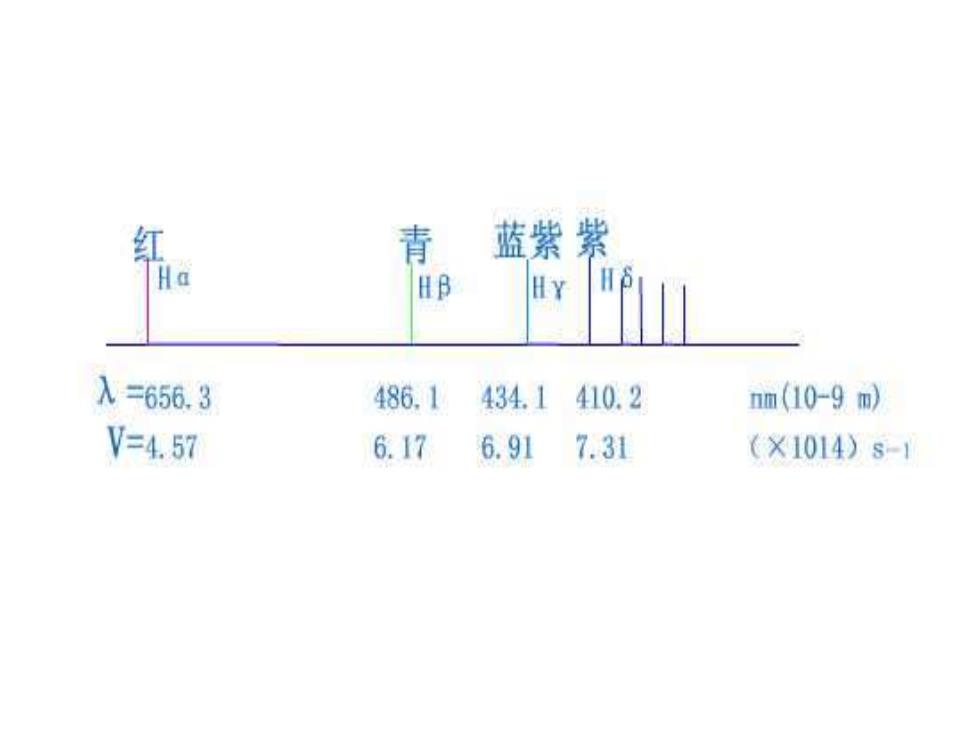
1.氢原子光谱 (1)实验事实:当极少量的高纯氢 气在高真空玻璃管中,加入高电压 使之放电,管中发出光束,使这种 光经过分光作用。在可见光区得到 四条颜色不用的谱线,如下图所示 这种光谱叫做不连续光谱或线状光 谱。所有的原子光谱都是线性光谱
1.氢原子光谱 • (1)实验事实:当极少量的高纯氢 气在高真空玻璃管中,加入高电压 使之放电,管中发出光束,使这种 光经过分光作用。在可见光区得到 四条颜色不用的谱线,如下图所示, 这种光谱叫做不连续光谱或线状光 谱。所有的原子光谱都是线性光谱
红 青蓝紫紫 Ha HB Hy 入=656.3 486.1 434.1410.2 nm(10-9m V=4.57 6.17 6.917.31 (×1014)s-1

1.氢原子光谱 ·(2)实验总结:1885年,瑞士一位中学物 理教师J.J.Balmar(巴尔多)指出,上述谱线的频 率符合下列公式: 11、 v=3.289X1015(2月s ·由此公式可算出: -当n=3时,是Ha的频率 -当n=4时,是HB的频率 -当n=5时,是HY的频率 -当n=6时,是H8的频率
1.氢原子光谱 • (2)实验总结: 1885年,瑞士一位中学物 理教师J.J.Balmar(巴尔多)指出,上述谱线的频 率符合下列公式: ν=3.289╳1015( )s-1 • 由此公式可算出: –当n=3时,是Hα的频率 –当n=4时,是Hβ的频率 –当n=5时,是Hγ的频率 –当n=6时,是Hδ的频率 2 2 1 2 1 n −

2.Bohr理论: ·1913年,丹麦物理学家N.Bohr首次 认识到氢原子光谱与结构之间的内 在联系,并提出了氢原子结构模型。 并用经典的牛顿力学推导了结论
2.Bohr理论: • 1913年,丹麦物理学家N.Bohr首次 认识到氢原子光谱与结构之间的内 在联系,并提出了氢原子结构模型。 并用经典的牛顿 力学推导了结论
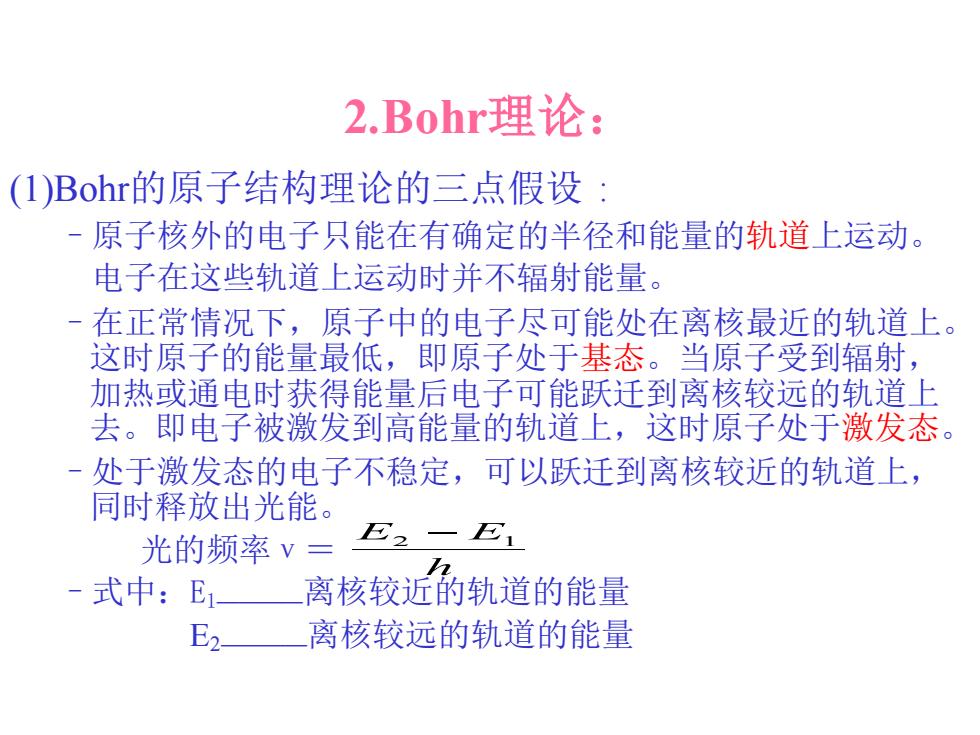
2.Bohr理论: (1)Bohr的原子结构理论的三点假设: -原子核外的电子只能在有确定的半径和能量的轨道上运动。 电子在这些轨道上运动时并不辐射能量。 在正常情况下,原子中的电子尽可能处在离核最近的轨道上。 这时原子的能量最低,即原子处于基态。当原子受到辐射, 加热或通电时获得能量后电子可能跃迁到离核较远的轨道上 去。即电子被激发到高能量的轨道上,这时原子处于激发态。 -处于激发态的电子不稳定,可以跃迁到离核较近的轨道上, 同时释放出光能。 光的频率V= E2一E1 -式中:E 离核较近的轨道的能量 E2 离核较远的轨道的能量
(1)Bohr的原子结构理论的三点假设 : –原子核外的电子只能在有确定的半径和能量的轨道上运动。 电子在这些轨道上运动时并不辐射能量。 –在正常情况下,原子中的电子尽可能处在离核最近的轨道上。 这时原子的能量最低,即原子处于基态。当原子受到辐射, 加热或通电时获得能量后电子可能跃迁到离核较远的轨道上 去。即电子被激发到高能量的轨道上,这时原子处于激发态。 –处于激发态的电子不稳定,可以跃迁到离核较近的轨道上, 同时释放出光能。 光的频率ν= –式中:E1————离核较近的轨道的能量 E2————离核较远的轨道的能量 2.Bohr理论: h E2 − E1

·轨道 ·基态、激发态 。引入量子数一n,1、2、3
• 轨道 • 基态、激发态 • 引入量子数- n , 1 、 2 、3

2.Bohr理论: Bohr在其三点假设的基础上,运用牛顿力学定律 推算出下列关香戎: r=aon E=一 n2 1 KJ.mol-1 v=3.29×1015( n2-n2)s-1 (n1<n2) 式中:r一氢原子轨道的半径,ao=0.053纳米 (玻尔半径) E—氢原子轨道的能量 v一氢原子中电子由高能态跃迁到低能 态时辐射光的平率一正整数(自然数,量 子数)
Bohr在其三点假设的基础上,运用牛顿力学定律 推算出下列关系式: r=a0n 2 E=- KJ.mol-1 ν=3.29╳1015( )s- 1 (n1<n2) 式中:r——氢原子轨道的半径,a0=0.053纳米 (玻尔半径) E——氢原子轨道的能量 ν——氢原子中电子由高能态跃迁到低能 态时辐射光的平率 n——正整数(自然数,量 子数)。 2.Bohr理论: 2 1312 n 2 2 2 1 1 1 n n −

2.Bohr理论: 1 1 ·根据v=3.29X1015( 2 2 )s1 在可见光区: n 当n1=2,n2=3 为Ha谱线的频率 n2=4 为HB谱线的频率 n2=5 为Y谱线的频率 n2=6 为Hδ谱线的频率 在红外光区: 当n1=3,n2=4,5,6,7有一组谱线 在紫外光区: 当n1=3,n2=2,3,4,5也有一组谱线
• 根据ν=3.29╳1015( )s- 1 在可见光区: 当n1 =2, n2 =3 为Hα谱线的频率 n2 =4 为Hβ谱线的频率 n2 =5 为Hγ谱线的频率 n2 =6 为Hδ谱线的频率 在红外光区: 当n1 =3,n2 =4,5,6,7有一组谱线 在紫外光区: 当n1 =3, n2 =2,3,4,5也有一组谱线 2.Bohr理论: 2 2 2 1 n 1 n 1 −

2.Bohr理论: (3)玻尔理论的贡献和局域性: -贡献: ·成功的解释了氢原子光谱。 ·提出了主量子数n和能级的重要概念,为 近代原子结构的发展作出一定的贡献。 -局限性: ·不能说明多电子原子光谱和氢原子光谱的 精细结构; ·不能说明化学键的本质
(3)玻尔理论的贡献和局域性: – 贡献: • 成功的解释了氢原子光谱。 • 提出了主量子数n和能级的重要概念,为 近代原子结构的发展作出一定的贡献。 – 局限性: • 不能说明多电子原子光谱和氢原子光谱的 精细结构; • 不能说明化学键的本质。 2.Bohr理论: