
§4活化能与元反应速率理论简介 阿伦尼乌斯方程 温度对反应速率的影响 纯经验关系式一范特霍夫规则: k0=y或 k7+10m=y Y=24 KT dlnK.△U m dink:E dT RT 和K=k dT RT j=?范特霍夫没解决,Arrhenius提出j= 0 得到Arrhenius方程: dln Es dT RT2
§4 活化能与元反应速率理论简介 2 ~ 4 1 0 1 0 = = = + + n T T n T T k k k k 或 一、阿伦尼乌斯方程 —— 温度对反应速率的影响 纯经验关系式 —— 范特霍夫规则: j R T E T k k k K R T U T K c c = = + = − + 2 2 r m d dln d dln 和 j = ?范特霍夫没解决, Arrhenius提出 j = 0 得到Arrhenius方程: 2 a d dln RT E T k =
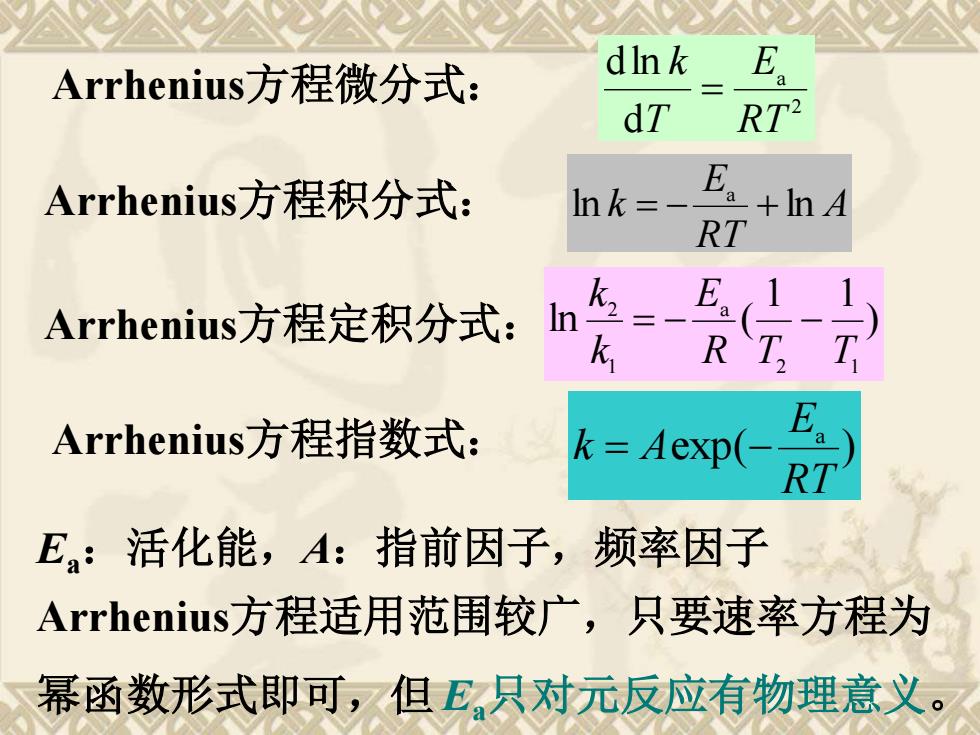
Arrhenius方程微分式: dInk dT RT2 Arrhenius方程积分式: Ink=- E。+nA RT Arrhenius方程定积分式: In k Arrhenius方程指数式: k Aexp(- a RT E:活化能,A:指前因子,频率因子 Arrhenius方程适用范围较广,只要速率方程为 幂函数形式即可,但E只对元反应有物理意义
2 a d dln RT E T k Arrhenius方程微分式: = Arrhenius方程积分式: A RT E ln k ln a = − + Arrhenius方程指数式: exp( ) a RT E k = A − Ea:活化能,A:指前因子,频率因子 Arrhenius方程适用范围较广,只要速率方程为 幂函数形式即可,但 Ea只对元反应有物理意义。 Arrhenius方程定积分式: ) 1 1 ln ( 2 1 a 1 2 R T T E k k = − −

1.元反应活化能 Arrhenius反应速率理论假设: (1)只有活化分子碰撞才是有效碰撞; (2)活化分子的平均能量与普通分子的平均 能量差称为活化能; (3)活化分子碰撞先形成“(中间)活化状态” 然后形成产物; (4)活化能与温度无关,与反应性质有关; (5)指前因子与分子的碰撞频率有关
1.元反应活化能 Arrhenius反应速率理论假设: (1)只有活化分子碰撞才是有效碰撞; (2)活化分子的平均能量与普通分子的平均 能量差称为活化能; (3)活化分子碰撞先形成“(中间)活化状态”, 然后形成产物; (4)活化能与温度无关,与反应性质有关; (5)指前因子与分子的碰撞频率有关
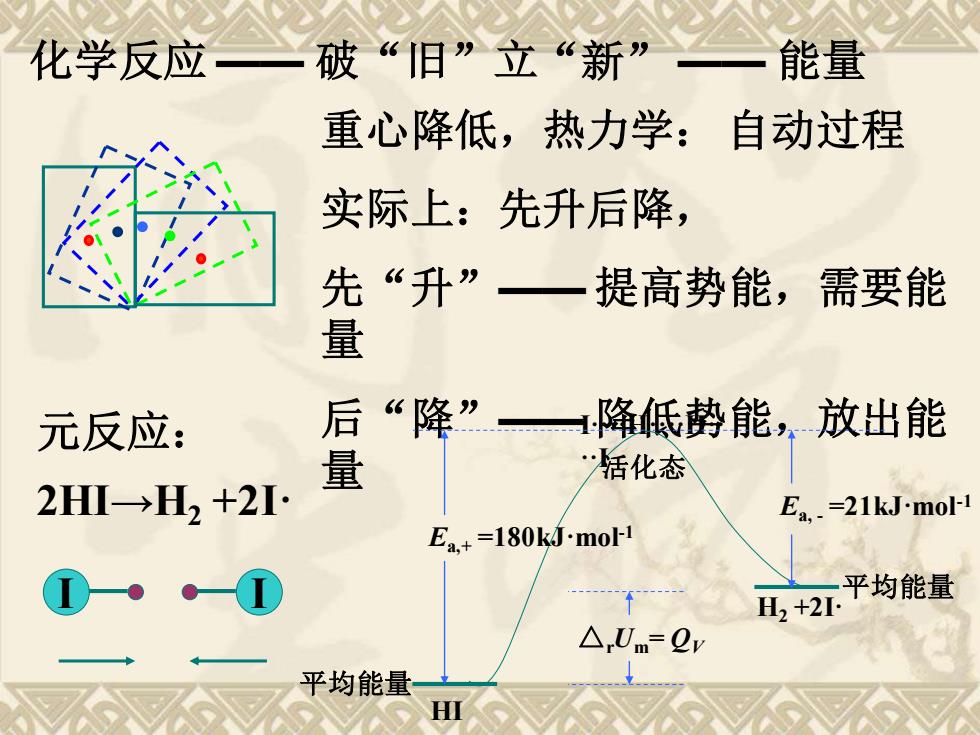
化学反应 破“旧”立“新” 能量 重心降低,热力学:自动过程 实际上:先升后降, 先“升”一提高势能,需要能 量 元反应: 后“降”降低势能,放出能 量 活化态 2H→H2+2I· Ea.=21kJ-mol-1 Ea.+=180kJ.mol-1 山+2平均能量 △,Um=2 平均能量 HⅢ
化学反应 —— 破“旧”立“新” —— 能量 重心降低,热力学: 自动过程 实际上:先升后降, 先“升”—— 提高势能,需要能 量 后“降”—— 降低势能,放出能 量 元反应: 2HI→H2 +2I· I I 平均能量 HI 平均能量 H2 +2I· I····H····H·· ··I活化态 Ea,+ =180kJ·mol-1 Ea, - =21kJ·mol-1 △rUm= QV

作用物跨越“能峰”→产物,“能峰”高低活 化能 “能峰”只适于元反应; Ead-Ea=2 一反应热效应 严格E,应与温度有关,由三参量经验式P33)得: Ea=E+mRT,E与温度关 则: E,≡-R d(1/T) E,400kJmo1,反应困难; 多数反应:40kJmo1<E,<400kJmo1;
作用物跨越 “能峰” →产物, “能峰”高低→活 化能 “能峰”只适于元反应; Ea,+-Ea, - = Q —— 反应热效应 严格Ea应与温度有关,由三参量经验式(P383)得: Ea = E + mRT, E与温度无关, 则: − d(1/ ) dln a T k E R Ea 400kJ·mol-1,反应困难; 多数反应:40kJ·mol-1 < Ea< 400kJ·mol-1;

2.活化能的作用 对元反应:反应活化能低,活化 分子多,反应快;反之,反应慢。 活化能决定温度对反应速率的影响程度,活化 能大,反应对温度敏感。(dlnk/dT=(E,/RT) ※改变温度可以改变反应速率。 ※改变活化能反应速率变化更明显。 热活化,光活化,机械活化,电活化, 实质:改变反应途径
2. 活化能的作用 N E 对元反应:反应活化能低,活化 分子多,反应快;反之,反应慢。 活化能决定温度对反应速率的影响程度,活化 能大,反应对温度敏感。(dlnk/dT) = (Ea /RT2 ) ※ 改变温度可以改变反应速率。 ※ 改变活化能反应速率变化更明显。 热活化,光活化,机械活化,电活化,· · · 实质:改变反应途径

3.阿伦尼乌斯方程的应用 ★求实验活化能:图解法,计算法, 对元反应求出实验活化能; 对非元反应求出(实验)表观活化能;P384 表观活化能无“能峰”的意义。 ★已知活化能值和某一温度(T)下的速率常数 (k),则可求出另一温度(T)下的速率常数 (k2)。(定积分式)
3. 阿伦尼乌斯方程的应用 ★ 求实验活化能:图解法,计算法, 对元反应求出实验活化能; 对非元反应求出(实验)表观活化能;P384 表观活化能无“能峰”的意义。 ★ 已知活化能值和某一温度(T1 )下的速率常数 (k1 ) ,则可求出另一温度(T2 )下的速率常数 (k2 ) 。(定积分式)

阿氏方程对有非幂函数速率方程的反应不适用 所以,温度对反应速率的影响形式多样P385图)。 二、简单碰撞理论(SCT) 1.双分子碰撞理论 双分子反应A+F→产物,假设: ◆反应物分子无内部结构和内部自由度的刚性 球,相互无作用,碰撞完全弹性; 反应分子必须通过碰撞才可能发生反应; 活化碰撞才有效;
阿氏方程对有非幂函数速率方程的反应不适用。 所以,温度对反应速率的影响形式多样(P385图)。 二、简单碰撞理论(SCT) 1. 双分子碰撞理论 双分子反应A+ F→产物,假设: ◆ 反应物分子无内部结构和内部自由度的刚性 球,相互无作用,碰撞完全弹性; ◆ 反应分子必须通过碰撞才可能发生反应; ◆ 活化碰撞才有效;

活化碰撞 碰撞分子对的能量达到或超过 某一定值ε(称为阈能)时,反应才能发生; ◆在反应过程中,反应分子的速率分布始终遵守 Maxwell-Boltzmann分布。 气体分子运动理论→单位体积内,单位时间作 用物分子碰撞次数一碰撞数 (Z) (1)异种分子碰撞: 1/2 NANE D 8πRT NANE 1000 1000
活化碰撞——碰撞分子对的能量达到或超过 某一定值ε0 (称为阈能)时,反应才能发生; ◆ 在反应过程中,反应分子的速率分布始终遵守 Maxwell-Boltzmann分布。 气体分子运动理论→单位体积内,单位时间作 用物分子碰撞次数—— 碰撞数(Z) A F 1/ 2 M 2 A F AF 1/ 2 A F A F 2 A F A,F 8 1000 1000 8 2 N N N N D R T M M M M R T d d Z = + + = (1)异种分子碰撞:

1/2 1/2 8πRT N,= NANE LDKE 8πRT =cL 1000 1000 CACE My .r= dc=1=- dt y dt 1 dN.g-exp( VL dt L = DXEL 1000 .k= DRrL 1000 ep(-后7)Aep(-7) .A= Ao∝T12 1000 与三参量公式比较(P386)。m三1/2
c L V n L N i i i = = A F 1/ 2 M 2 A F 2 A F 1/ 2 M 2 A ,F A F 8 1000 1000 8 c c R T N N L D R T Z D = = , exp( ) d 1 d d 1 d d d A A A A ,F c R T E q q L Z t N t V L n t V c r = − = − = − = = − A F c A F 1/ 2 M 2 A F exp( ) 8 1000 kc c R T E c c D L R T r − = = exp( ) exp( ) 8 1000 c c 1/ 2 M 2 A F R T E A R T D L R T E k − = − = 1/ 2 1/ 2 0 1/ 2 M 2 A F 8 1000 Z T A T D L R T A = = 与三参量公式比较(P386)。m = 1/2