
第三章 化学平衡热力学原理
第三章 化学平衡热力学原理

由△G的符号可判断过程的方向,△G是化 学反应体系中产物Gibbs自由能与作用物Gibbs自 由能之差,随着反应进行△G,趋向于零,反应 趋向平衡。当外界条件发生改变时,原平衡被破 坏,即发生平衡移动,直至达到新条件下的新平 衡。那么,平衡移动的方向?新平衡点(限度)? 与外界影响因素的关系?一本章要解决的问题
由△rGT,p的符号可判断过程的方向,△rGT,p是化 学反应体系中产物Gibbs自由能与作用物Gibbs自 由能之差,随着反应进行△rGT,p趋向于零,反应 趋向平衡。当外界条件发生改变时,原平衡被破 坏,即发生平衡移动,直至达到新条件下的新平 衡。那么,平衡移动的方向?新平衡点(限度)? 与外界影响因素的关系?——本章要解决的问题

§1.化学反应的等温方程式 一、化学反应等温方程式的导出 1.化学平衡的条件 T,卫 aA+dD-L-xX+yY 或0=2=∑yB 不作有效功的条件下,反应过程的任意瞬间: dGx,p=∑4edng=∑4B(yBd5) 得 =∑y4a=△,Gm和 T.p
§1. 化学反应的等温方程式 一、化学反应等温方程式的导出 1.化学平衡的条件 aA +d D ==== xX + yY 或 不作有效功的条件下,反应过程的任意瞬间: 0 ==== B B T, p T, p d d ( d ) GT , p = B nB = B B 得 B B r m , G G T p = = 和 = r Gm G T
反应过程中,发生变化→H也变化→G体变化 △Gm0,反应自动左移; △Gm=0,体系达到平衡 化学反应平衡的条件是: △,Gm △Gm=0 △,Gm=∑V4,=0 这是“量变”到“质变”的分界 点
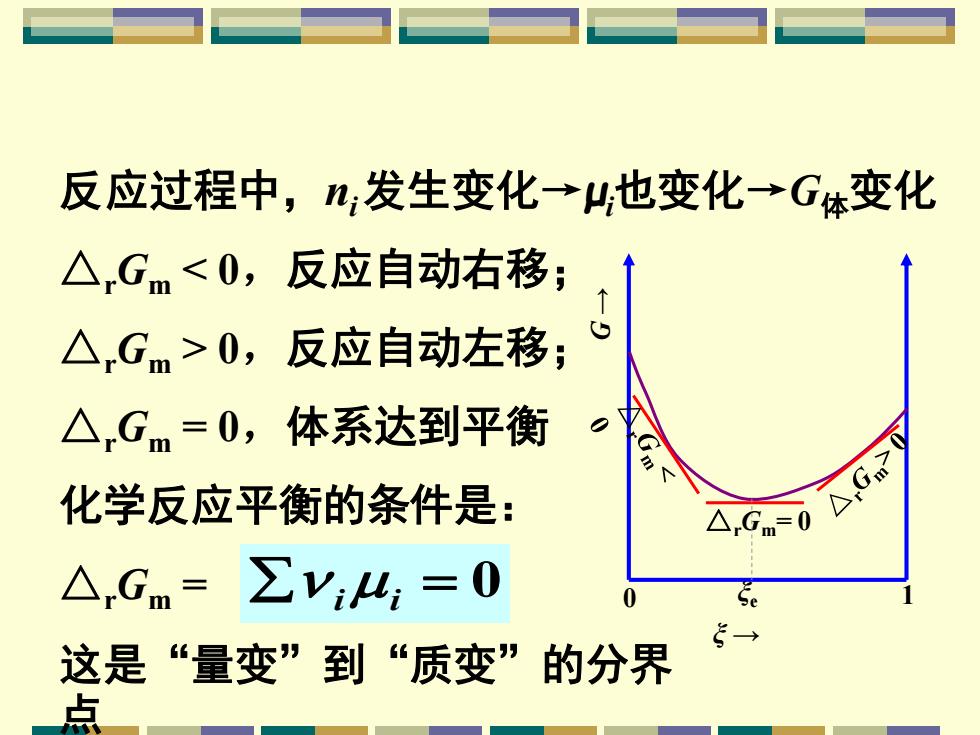
反应过程中,ni 发生变化→μi也变化→G体变化 △rGm= 0 G → ξ → 0 ξe 1 △rGm 0,反应自动左移; △rGm = 0,体系达到平衡 化学反应平衡的条件是: △rGm = 这是“量变”到“质变”的分界 点 i i = 0

-∑y4=-△Gm也被定义为“化学亲和势” “化学亲和势”描述了物质间化学反应的趋势, 贝特洛原理(早期: 反应放热(△HmO) 反应存在
− i i = −r Gm 也被定义为“化学亲和势” “化学亲和势” 描述了物质间化学反应的趋势, 贝特洛原理(早期) : 反应放热(△rHm 0) 反应存在 如何解释?

一△Gm=T△Sm一△Hm≥0,反应自动进行 当△Hm0时,△.Gm≤0,且|△Hm愈大, △Gm愈负,反应趋势愈大一满足贝氏原则 当△Hm|T△Sml,则△Gm≤0 一满足贝氏原则 若△Hml0一贝氏原则失效 当△Hm>0,△Sm0,满足贝氏原则 当△Hm>0,△Sm>0时, 若△Hm>T△Sm,则△Gm≤0一贝氏原则失效 若△Hm0一氵 满足贝氏原则
-△rGm= T△rSm - △rHm≥0,反应自动进行 当△rHm<0, △rSm>0时, △rGm≤0,且|△rHm |愈大, △rGm愈负,反应趋势愈大—— 满足贝氏原则 当△rHm<0, △rSm<0时: 若|△rHm |>|T△rSm |,则△rGm≤0 —— 满足贝氏原则 若|△rHm |<|T△rSm |,则△rGm>0 ——贝氏原则失效 当△rHm>0 ,△rSm<0时,△rGm>0,满足贝氏原则 当△rHm>0 ,△rSm>0时, 若△rHm >T△rSm,则△rGm≤0 ——贝氏原则失效 若△rHm <T△rSm ,则△rGm>0 —— 满足贝氏原则

2.均相化学反应等温方程式 ★气相反应 设为理想气体 aA+fF====xX+yY 4,=4°(T)+RTnP: AGm=∑y,4,=∑y,4(T)+∑y,RTIn Pi 令:∑y,ln=nJ8 J8— 标准压强商 则:△,Gm=△,GR+RTInJ9— 等温方程式
2.均相化学反应等温方程式 ★ 气相反应 设为理想气体 aA + f F ==== xX + yY = + p p T RT i i i ( ) ln = = + p p G T RT i i i i i i r m ( ) ln = p i i J p p 令: ln ln p J —— 标准压强商 G = G + RT J p 则: r m r m ln —— 等温方程式

化学反应达到平衡时,△Gm=0,则: RTIn(J)m=-△,G8=-∑y,4°(T)—只是T的函数 当T一定时,(J)确定,令(U)m=K9 称Ke为标准平衡常数,即△,G=-RTlnK9 且:A,Gm=-RTnK9+RTnJ9—等温方程式 J9=Πpr(p)2vK9=Π(p)a(p)2 蓍 (s)()H ()() ()(g)尸
化学反应达到平衡时,△rGm = 0,则: 注 意 RT ln(J p ) eq = −r Gm = − i i (T) ——只是T的函数 当T一定时, 确定,令 称 为标准平衡常数,即 且: —— 等温方程式 J p eq = Kp ( ) eq ( ) J p K p G = −RT Kp r m ln G = −RT Kp + RT J p r m ln ln f p a p p p y p x p p p p i i i J p p ( ) ( ) ( ) ( ) ( ) A F X Y = = − f p a p p p y p x p p p p i i i K p p eq eq eq eq eq ( ) ( ) ( ) ( ) ( ) ( ) A F X Y = = −

等温式用于判断过程(平衡)的方向和限度: △Gm=RTln J9>K,△Gm>0,反应(平衡)逆向移动 J<K9,△Gm<0,反应(平衡)正向移动 J9=K,△Gm=0,反应达到平衡,不移动
= p p K J r Gm RT ln J p Kp ,△rGm > 0,反应(平衡)逆向移动 J p Kp ,△rGm < 0,反应(平衡)正向移动 J p = Kp ,△rGm = 0,反应达到平衡,不移动 等温式用于判断过程(平衡)的方向和限度:

★液相反应 QA+fF====xX+yY 选择某一参考态后,化学势与活度的关系为: 4=参考态(T,p)+RTl血a 则△,Gm=∑y4=∑y,4套考态(T,p+∑y,RTna 令:∑y,n,=lnJ。 J。一活度商 则:△,Gm=∑y,参考态(T,p)+RTInJ。 压强对凝聚态影响很小,在压强不高时, 4套考态(T,P)≈4°(T)
★ 液相反应 aA + f F ==== xX + yY 选择某一参考态后,化学势与活度的关系为: i i T p RT ai = ( , )+ ln 参考态 a 令: i lnai = ln Ja J —— 活度商 G i i T p RT Ja r m = ( , )+ ln 参考态 则: 压强对凝聚态影响很小,在压强不高时, (T, p) (T) i i 参考态 G i i i i T p i RT ai r m = = ( , )+ ln 参考态 则