
§4.熵(S)及其应用 一、热功的转换效率与 热力学第二定律的经典表述 1.卡诺循环及可逆热机效率 高温热源(T) (1)恒温可逆膨胀 ,(2)绝热可逆膨胀 锅炉 T1一T2 太空 低温热源(T2) (3)恒温可逆压缩;(4)绝热可逆压缩 T2→T1
§4. 熵(S)及其应用 一、热功的转换效率与 热力学第二定律的经典表述 1. 卡诺循环及可逆热机效率 高温热源(T1) 锅 炉 太 空 低温热源(T2) (1)恒温可逆膨胀;(2)绝热可逆膨胀 T1 T2 (3)恒温可逆压缩;(4)绝热可逆压缩 T2→T1 Q1 Q2
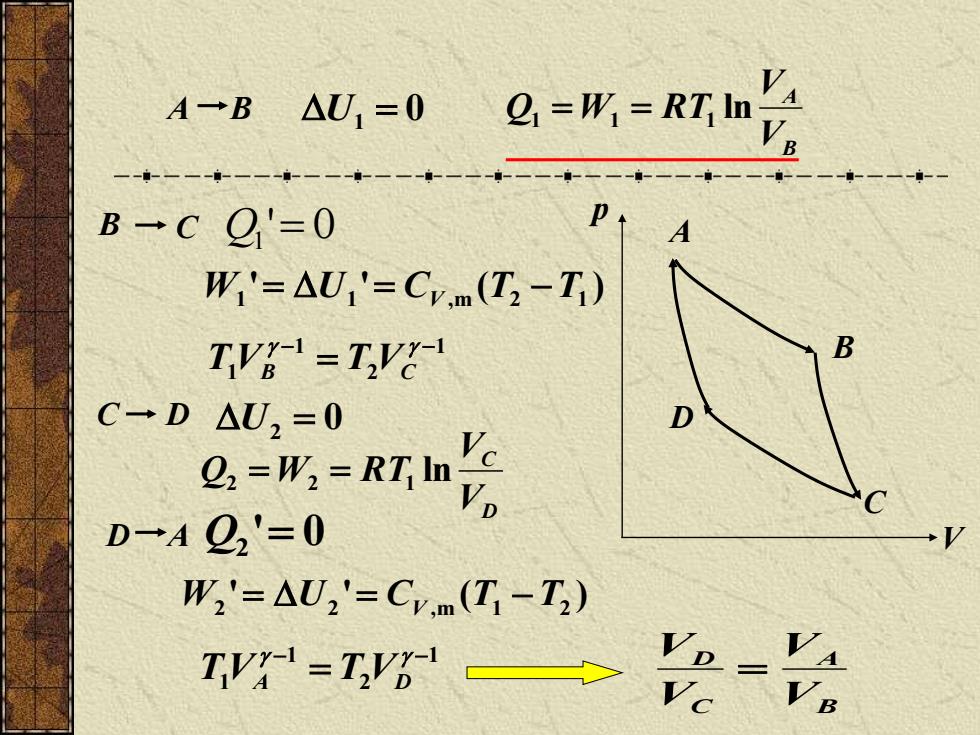
A-B△U,=0 V Q,=用=RT B→cQ'=0 W'=△U1'=C.m(T2-T) TVB-=TVg- C一D△U2=0 D Q.-W:-RTInyp ,'c D-A22'=0 W2'=△U2'=Cm(T-T2)
V p A B C C D B C Q1 ' = 0 ' ' ( ) W1 = U1 = C V , m T2 − T1 D U2 = 0 DC VV Q 2 = W2 = RT1 ln 1 2 1 1 − − = T VB T VC D A Q2 ' = 0 ' ' ( ) W2 = U 2 = C V , m T1 − T2 1 2 1 1 − − = T VA T VD BA CD VV VV = A B U1 = 0 BA VV Q1 = W1 = RT1 ln

e=g,+e.+0+0,=Q,+2,=Rr-In'0 三市 热机效率:7=”_2+2可道1- 21 21 热机 (1)T2不为绝对零度时,7<1。 (2)热功转换具有不可逆性。 功可100%转换成热,热不可能100%转换成功 (3)+9=0
W V V Q Q Q Q Q Q Q R T T B A = − = 1 + 2 + 1 '+ 2 '= 1 + 2 = ( 1 − 2 )ln (1)T2不为绝对零度时, (2)热功转换具有不可逆性。 功可100%转换成热,热不可能100%转换成功 r < 1。 (3) 0 2 2 1 1 + = T Q T Q 1 1 2 1 Q Q Q Q W + = − 热机效率: = 可逆 热机 ——— 1 1 2 T T −T

2.热力学第二定律的经典表述(见教材P208) 实质:自动过程都是不可逆的。 3.卡诺原理 在两个热源之间工作的热机中,可逆热 机效率最大。即:1≥1 ★在两个热源之间工作的一切可逆热机效率 相等。1r=1r ★在两个热源之间工作的可逆热机效率大于 切不可逆热机效率。1.>1r 则: g+g≤0
2. 热力学第二定律的经典表述 (见教材 P208) 实质:自动过程都是不可逆的。 3. 卡诺原理 在两个热源之间工作的热机中,可逆热 机效率最大。即:ηr≥η ★在两个热源之间工作的一切可逆热机效率 相等。ηr = ηr ★在两个热源之间工作的可逆热机效率大于 一切不可逆热机效率。 ηr >ηir 2 2 1 1 T Q T Q 则: + ≤0

二、任意可逆循环过程的热温商与熵函数 热温商:QT 对卡诺循环有:号+ 2=0 p 设任意可逆循环:A一B一A 每个小卡话猫环%% B 整个循环过程:户学,-0或%-0 f9.=9e+9nm=9).a-9)a=0
二、任意可逆循环过程的热温商与熵函数 热温商:Q/T 0 2 2 1 1 + = T Q T Q 对卡诺循环有: 设任意可逆循环:A B A 0 δ δ 1 1 + = + + i i i i T Q T Q 每个小卡诺循环: 整个循环过程: ) 0 δ ( r 1 = i= i i T Q ) 0 δ ( r = i i T Q 或 ) 0 δ ) ( δ ) ( δ ) ( δ ) ( δ ( r = r( ) + r( ) = r( ) − r( ) = B A B A A B B A T Q T Q T Q T Q T Q V p A B

即:2a-9o 令:d= T S:熵,熵变形式定义 则:鹘a=鹘n-ia=S,-s,=△s ※熵是状态函数,体系的容量性质; ※经可逆过程,熵变量dS=8 T ※δ2.=TdS,而δW=-pdV
r( ) r( ) ) δ ) ( δ ( = B A B A T Q T 即: Q 令: T Q S δ r d = 则: S S S S T Q T Q B A B A B A B A = = = − = ) d δ ) ( δ ( r( ) r( ) S : 熵,熵变形式定义 ※ 熵是状态函数,体系的容量性质; ※ 经可逆过程,熵变量 ; ※ ,而 T Q S δ r d = δQr = TdS δW = − pdV

三、熵增原则 1,任意不可逆过程的热温商与熵变的关系, 设可逆(r)与不可逆(r)两条途径 由第一定律得:dU,=δ2,+δW,dUr=δ2r+δWr 而dU=dUr,δW0÷9,9 不可逆循环有:工%0 B 又ds=2,故s>2 T
三、熵增原则 1. 任意不可逆过程的热温商与熵变的关系 V p A B r ir 设可逆(r)与不可逆(ir)两条途径 由第一定律得: r r r d i r δ i r δ i r dU = δQ + δW , U = Q + W d d , 而 Ur = Uir δWr δWirT Q T Q Q Q r i r r i r δ δ δ δ 不可逆循环有: 0 δ T Q T Q S δ r 又 d = ,故 T Q S δ ir d

2.克劳修斯(Clausius)不等式 因为有加5-观有山空,故西习 Clausius不等式,第二定律的数学表达式, T 热源(环境)温度。 3.自动过程的共同特征 自动过程:在指定条件下,不需要消耗外力 (热or功)而自行发生、进行的过程
2. 克劳修斯(Clausius)不等式 T Q S δ r 因为有 d = 和 ,故: ≥ T Q S δ ir d dS T ir δQ r Clausius不等式,第二定律的数学表达式, T—— 热源(环境)温度。 3. 自动过程的共同特征 自动过程:在指定条件下,不需要消耗外力 (热or功)而自行发生、进行的过程

实例 方向 推动力 限度 判据 传热 T高→T低 温差(△D△T-0 温度T 水流h高→h低水位差(△h)△h=0水位h 自动过程的逆过程都不能自动进行,要实现, 需要借助外力,所以, ▲自动过程是不可逆过程,反之不成立; ▲自动过程的推动力是强度性质差; ▲自动过程有推动力,有判据
实例 方向 推动力 限度 判据 传热 T高→ T低 温差(△T) △T= 0 温度T 水流 h高→ h低 水位差(△h ) △h = 0 水位h 自动过程的逆过程都不能自动进行,要实现, 需要借助外力,所以, ▲ 自动过程是不可逆过程,反之不成立; ▲ 自动过程的推动力是强度性质差; ▲ 自动过程有推动力,有判据

4.熵增原则 将AS屿号 比较,可判断过程可逆与否 (1)绝热可逆:ds=9=0,恒嫡过程 2)绝热不阿逆:sg050箱增 T (3)隔离体系:δQ=δw=0 ò0=0,dS隔多,6w=0无外力作用 故dS9,或△S% 自动 自动 熵判据 隔离体系进行的自动过程使体系熵增
4. 熵增原则 将△S与 比较,可判断过程可逆与否 T Q (1)绝热可逆: ,恒熵过程 (2)绝热不可逆: ,dS >0 熵增 (3)隔离体系: , dS隔 ≥0 , 无外力作用 故 dS隔 ≥0 ,或△S隔 ≥0 熵判据 隔离体系进行的自动过程使体系熵增 0 δ d r = = T Q S 0 δ d ir = T Q S δQ = δW = 0 δQ = 0 ir r δW = 0 自动 平衡 自动 平衡