
②规定熵或标准熵 a)规定熵(标准熵): 在标准状态下(T,P),1mol纯物质的熵值 S) m:1mol; 0:标态; 298K:温度 b)化学反应熵的计算 (1) 由规定嫡计算化学反应的△SM29sK △,S228K)=(∑y,S)产(∑Si)反应物
1 ②规定熵或标准熵 a)规定熵(标准熵): 在标准状态下(T,P θ),1mol 纯物质的熵值 S m(298K) b)化学反应熵的计算 (1)由规定熵计算化学反应的Δr S m(298K) Δr S m(298K) =( ) , m j j j S 产物 - ( ) , m i i i S 反应物 m: 1mol;θ:标态; 298K:温度
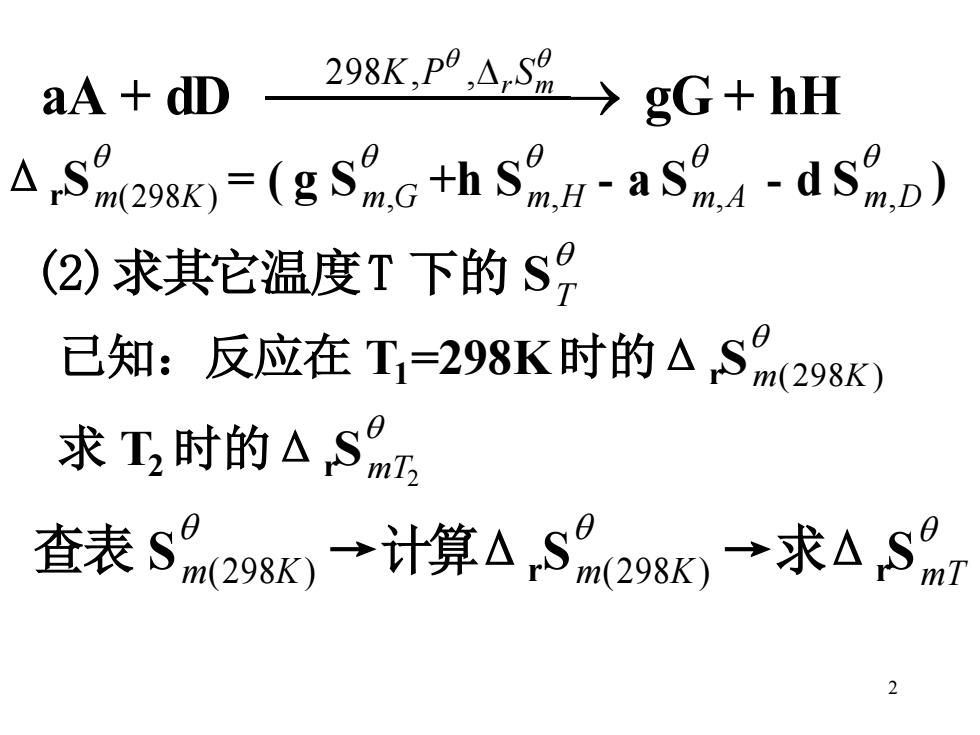
aA dD 298Kp4s8→gG+hH A S(298K)=(gSthSdmo) (2)求其它温度T下的S 己知:反应在T1=298K时的△SM298K 求工,时的△S9m 查表S9m28K)→计算△rS%298K→求△rSr 2
2 aA + dD ⎯⎯⎯⎯ ⎯→ 298K,P , r S m gG + hH Δr S m(298K) = ( g S m,G +h S m,H - a S m,A - d S m,D ) (2)求其它温度T 下的 S T 已知:反应在 T1 =298K时的Δr S m(298K) 求 T2 时的Δr S m T2 查表 S m(298K) →计算Δr S m(298K) →求Δr S m T
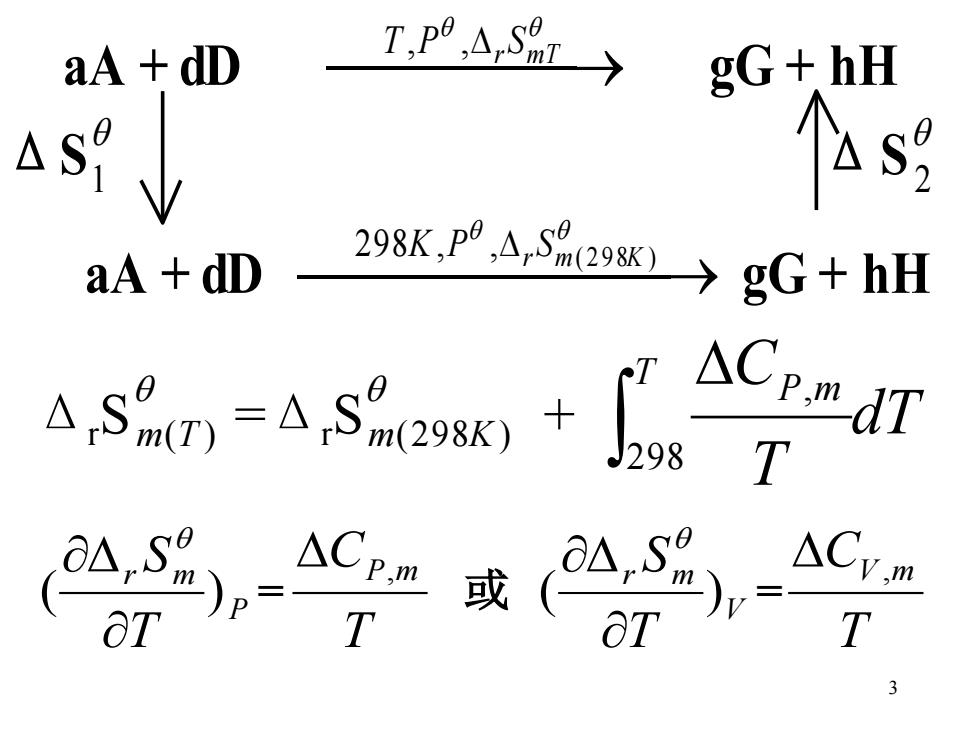
aA dD Tp9,d→ gG+hH s aA dD 298K,p9,A,S9298x →gG+hH T △Cpm T T 3
3 aA + dD ⎯⎯⎯⎯→ r m T T ,P , S gG + h H ΔS 1 ΔS 2 aA + dD ⎯⎯⎯⎯⎯ ⎯→ ( 298 ) 298 , , r m K K P S gG + h H Δ r S m(T ) =Δ r S m(298K) + dT T T CP m 298 , P r m T S ( ) = T CP,m 或 V r m T S ( ) = T CV ,m

联想:( 2).-sc 当ACrm0时,△m,△H与T无关 适用范围:等TP,等TV化学变化和相变化 说明:若有相变化发生,需考虑可逆相变化 的熵值 AS A(S,T→0) →A(1,T2) 个 A(S,T)A→A(1,T)
4 联想: P r m T H ( ) =CP,m 当CP,m =0 时,Δr S m ,Δr H m 与 T无关 适用范围:等 TP,等 TV 化学变化和相变化 说明:若有相变化发生,需考虑可逆相变化 的熵值 ΔS1 ΔS3 A(s,T1 )⎯ ⎯S2 → A(l,T1 ) A(s,T→0) ⎯⎯→ S A(l,T2 )
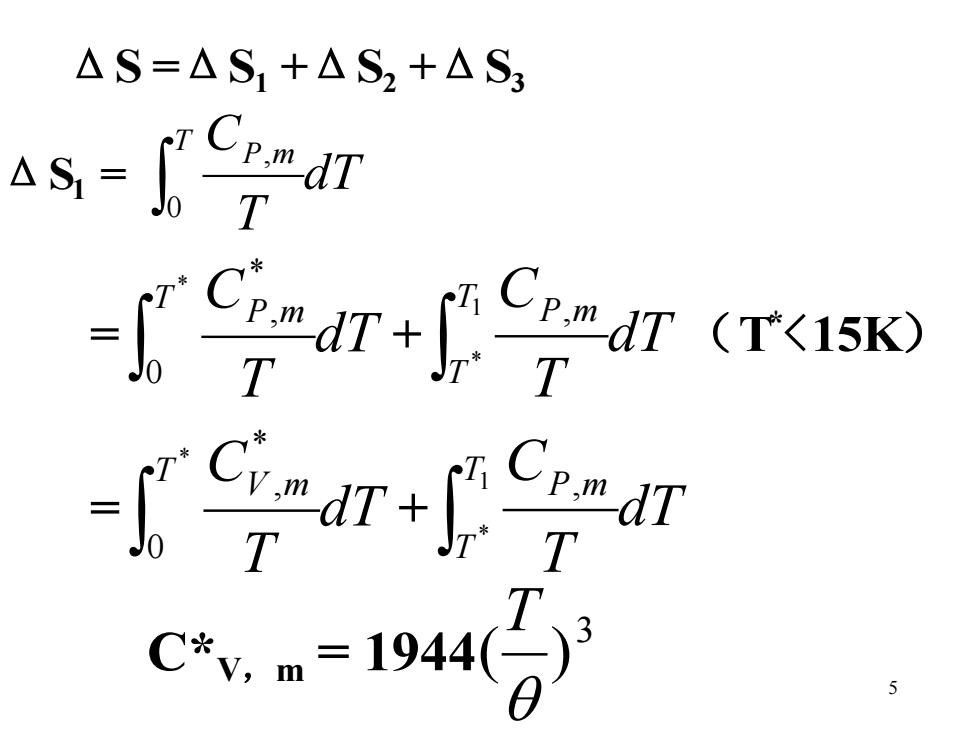
△S=△S1+△S2+AS3 △S= T CPm dT T C7+ pm dT T 5
5 ΔS =ΔS1 +ΔS2 +ΔS3 ΔS1 = dT T T CP m 0 , = dT T T CP m * 0 * , + dT T T C T P m 1 * , (T * <15K) = dT T T CV m * 0 * , + dT T T C T P m 1 * , C*V,m = 1944 3 ( ) T

△S2= △s,= Cpm)dT T T §2.7熵的统计意义一物理意义 1877年玻兹曼研究分子运动论的统计现象后 给出熵的物理意义 1.熵是体系内混乱程度的度量 体系内部的无序性 S的大小反映了体系内部大量质点运动的 混乱程度 1)热传导:高温T高—一 高能级粒子数多 低温T低 低能级粒子数多
6 ΔS2 = T1 Hm l s ΔS3 = dT T T C T P m l 2 1 , ( ) §2.7 熵的统计意义——物理意义 1. 熵是体系内混乱程度的度量 体系内部的无序性 S 的大小反映了体系内部大量质点运动的 混乱程度 1)热传导:高温 T 高——高能级粒子数多 低温 T 低——低能级粒子数多 1877 年玻兹曼研究分子运动论的统计现象后 给出熵的物理意义

微观:有序无序 宏观:向熵增加的方向变化 2)气体真空膨胀 开始:较有序,不混乱 终态:无序,混乱 微观:向混乱程度增加的方向变 宏观:△S>0,向熵增加的方向变化 3) H,O①与H,Og)的△S比较 由无序运动的程度 比较混乱度:Smg)〉Sm) 7
7 微观:有序→无序 宏观:向熵增加的方向变化 2)气体真空膨胀 开始:较有序,不混乱 终态:无序,混乱 微观:向混乱程度增加的方向变 宏观:ΔS> 0,向熵增加的方向变化 3)H2O(l)与 H2O(g)的ΔS 比较 比较混乱度:Sm(g)> Sm(l) 由无序运动的程度
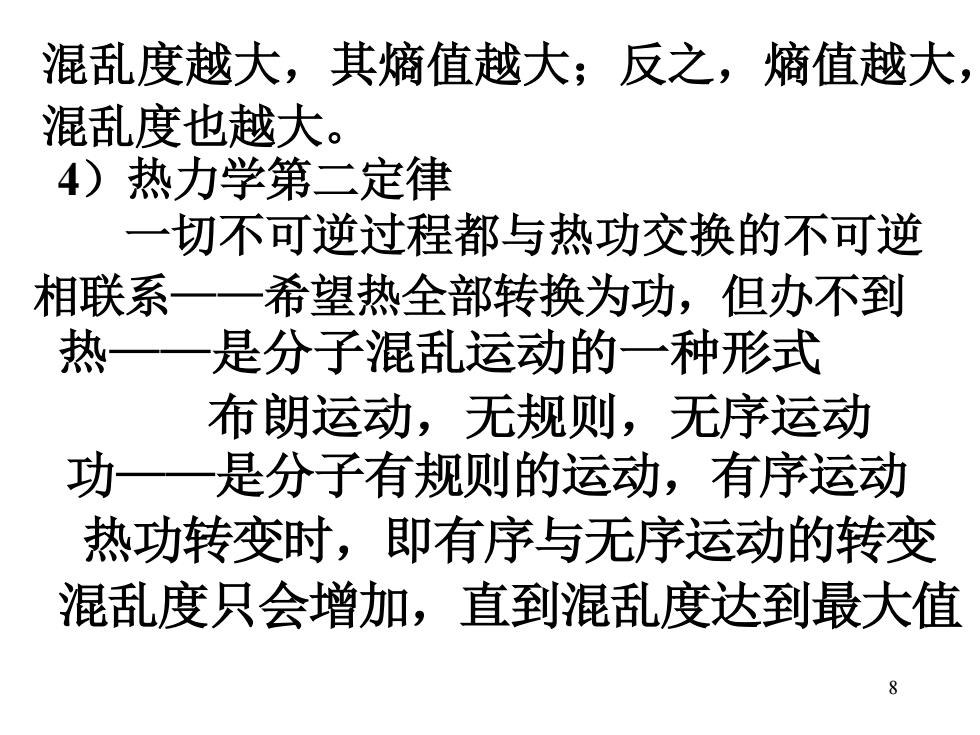
混乱度越大,其熵值越大;反之,熵值越大 混乱度也越大。 4)热力学第二定律 一切不可逆过程都与热功交换的不可逆 相联系一一希望热全部转换为功,但办不到 热 是分子混乱运动的一种形式 布朗运动,无规则,无序运动 功一一是分子有规则的运动,有序运动 热功转变时,即有序与无序运动的转变 混乱度只会增加,直到混乱度达到最大值
8 4)热力学第二定律 一切不可逆过程都与热功交换的不可逆 相联系——希望热全部转换为功,但办不到 热——是分子混乱运动的一种形式 布朗运动,无规则,无序运动 功——是分子有规则的运动,有序运动 混乱度越大,其熵值越大;反之,熵值越大, 混乱度也越大。 热功转变时,即有序与无序运动的转变 混乱度只会增加,直到混乱度达到最大值

一切不可逆过程都是向混乱度增加方向进行 热力学第二定律的本质 第二定律又与熵函数有关 熵函数是体系混乱度的一种度量 2.玻兹曼公式(Boltzmann) 1)宏观状态,微观状态 宏观状态:宏观物理量,P,V,T等确定的量 微观状态:能量,空间位置 体系确定的宏观状态是由体系不同微观 状态体现的
9 2. 玻兹曼公式(Boltzmann) 1)宏观状态,微观状态 一切不可逆过程都是向混乱度增加方向进行 ——热力学第二定律的本质 第二定律又与熵函数有关 熵函数是体系混乱度的一种度量 宏观状态:宏观物理量,P,V,T 等确定的量 微观状态:能量,空间位置 体系确定的宏观状态是由体系不同微观 状态体现的

确定的微观状态需一个很大的微观状态数2 熵增加原理:△S≥0 S与2存在某种平衡的对应的关系 2)玻兹曼公式(1876年) S=kLn2一玻兹曼公式 R k:玻兹曼常数,k= =1.3806×1023J/K 2:微观状态数 2越大,S越大 S的统计意义:混乱度 10
10 熵增加原理:ΔS ≥0 2) 玻兹曼公式(1876 年) S = kLnΩ——玻兹曼公式 k:玻兹曼常数,k = L R = 1.3806×10-23J/K Ω:微观状态数 S 的统计意义:混乱度 确定的微观状态需一个很大的微观状态数Ω S 与Ω存在某种平衡的对应的关系 Ω越大,S 越大