V)理气的混合熵 1)等T,V混合 卫aTy+BTV I”→,£,IV n=nA+ng P=PA+PB 等T:△UA=0,△UB=0,△U=0 △H=0,△H=0,△U=0 始态 终态 A T,V,PA T,V,PA △S=0 B T,V,Pe T,V,PB 1
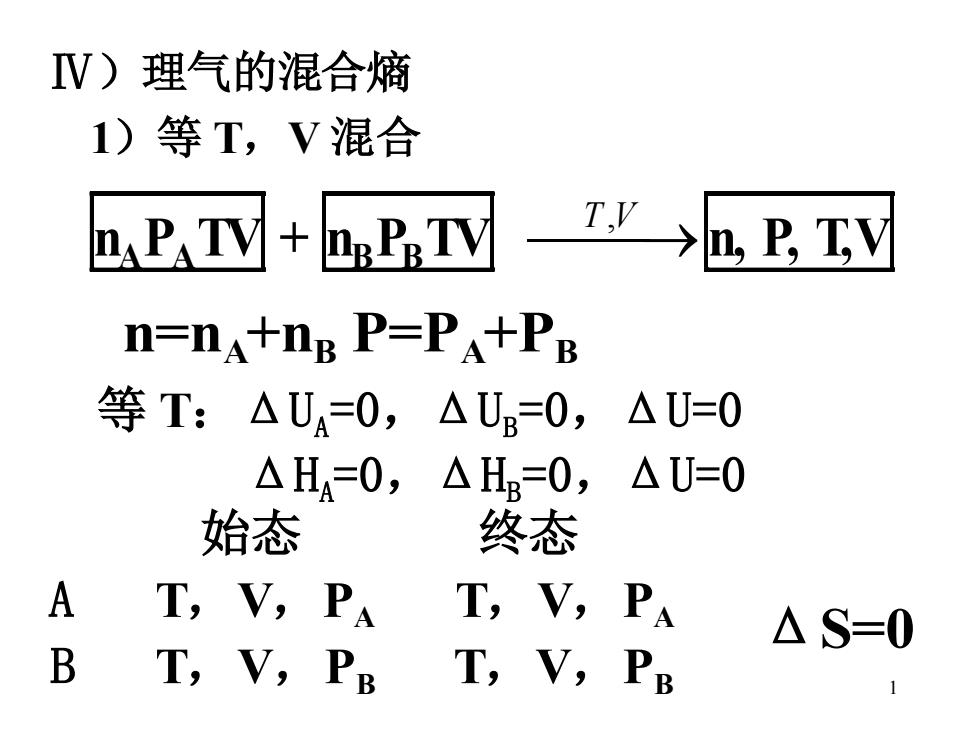
1 Ⅳ)理气的混合熵 1)等 T,V 混合 nA PA TV + nB PB TV ⎯T ⎯,V →n, P, T,V n=nA +nB P=PA +PB 等 T:ΔUA = 0,ΔUB = 0,ΔU=0 ΔHA = 0,ΔHB = 0,ΔU=0 始态 终态 A T,V,PA T,V,PA B T,V,PB T,V,PB ΔS=0

说明:a)始终态未变△S=0 b)两种不同理气等TV混合△S=0 c)相同理气混合相当于压缩,△S≠0 2)等T(P)的混合 na VeTP+ne VeTP ip >n,V,T,P n=na+nB,P=PA+PB2 V=VA+VB 始态 终态 A VA,T,P T,V,PA V=V+VB B VB,T,P T,V,PB P=PA+PB
2 说明:a)始终态未变ΔS=0 b)两种不同理气等 TV 混合ΔS=0 c)相同理气混合相当于压缩,ΔS≠0 2)等 T(P)的混合 n=nA +nB , P=PA +PB , V=VA + VB 始态 终态 A VA,T,P T,V,PA V=VA +VB B VB,T,P T,V,PB P=PA +PB nA VB TP + nB VB TP ⎯T ⎯,P →n , V , T , P
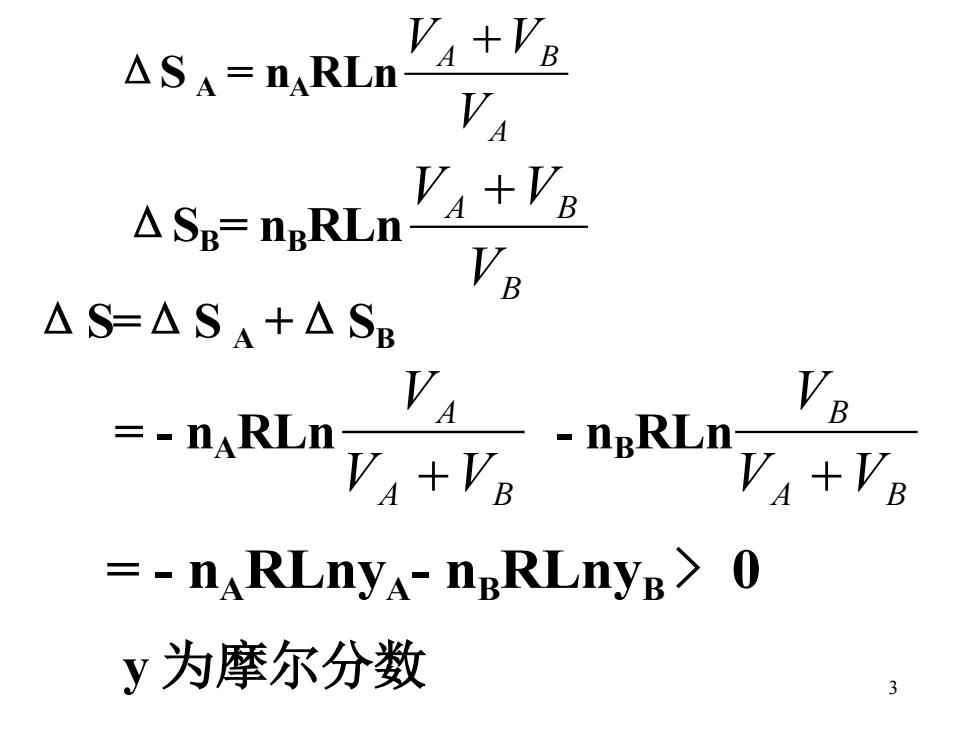
Va +VB △SA=n4RLn Va VA+VB A SB=neRLn VB AS=△SA+ASB =-an,a Va =-nARLnyA-nERLnyB >0 y为摩尔分数 3
3 ΔS A = nA RLn A A B V V +V ΔSB = nB RLn B A B V V +V ΔS=ΔS A +ΔSB = - nA RLn A B A V V V + - nB RLn A B B V V V + = - nA RLnyA- nB RLnyB > 0 y 为摩尔分数

△S环=Q体/T=0 Q体=0 △S总=△S体=-n4 RLnyA-ngRLnyE>0 绅业凹缅最Lb婚号 AS-RnLny>0 说明:a)等T,P混合,△S↑,V:↑,活动空 间↑,混乱度增大 b)若为同种理气等T,P 状态没有发生变化混合△$=0
4 ΔS 环=-Q 体/T= 0 ΔS 总=ΔS 体= - nARLnyA- nBRLnyB >0 几种不同理气等 T,P混合: ΔS= -R i n i ni Lny > 0 说明:a)等 T,P 混合,ΔS↑ ,Vi↑,活动空 间↑,混乱度增大 b)若为同种理气等 T, P Q 体=0 状态没有发生变化 混合ΔS=0

△S 等T,V 等T,P 不同理气 △S=0 n aS-R∑n,Lny 相同理气 △S≠0 △S=0 2.相变化过程的熵变 相变化:在一定条件下,物质从一种聚集态 变到另一种聚集态 聚集态:汽,液,固,g,1,s表示 1)可逆相变化: 5
5 2. 相变化过程的熵变 相变化:在一定条件下,物质从一种聚集态 变到另一种聚集态 聚集态:汽,液,固,g,l,s 表示 1)可逆相变化: c) ΔS 等 T,V 等 T,P 不同理气 ΔS= 0 ΔS= -R i n i ni Lny 相同理气 ΔS≠0 ΔS= 0

①定义:发生在两相平衡共存的T,P下的相变 可逆相变 例:H0(0) IP→H20(g) T=373K,P*=P9=101325Pa T=298K,P*=3168Pa T体=T环,P体=P环=P外 例:P时的平衡T,熔点,沸点,晶型转变点 为可逆相变 6
6 例: H2 O (l) ⎯T ⎯,P → H2 O (g) T=373K, P*=Pθ=101325Pa T=298K, P*=3168Pa T 体= T 环, P 体=P 环=P 外 例:P θ时的平衡 T,熔点,沸点,晶型转变点 ——为可逆相变 发生在两相平衡共存的 T,P 下的相变 ——可逆相变 ①定义:
②可逆相变的△S计算 可逆相变:相变潜热Q T T △S=△S体+△S环=0 例:1molH20() T,P,△S=? →H20(S) T=273K,P=101325Pa 已知:疑固热为-6004J·molH 7
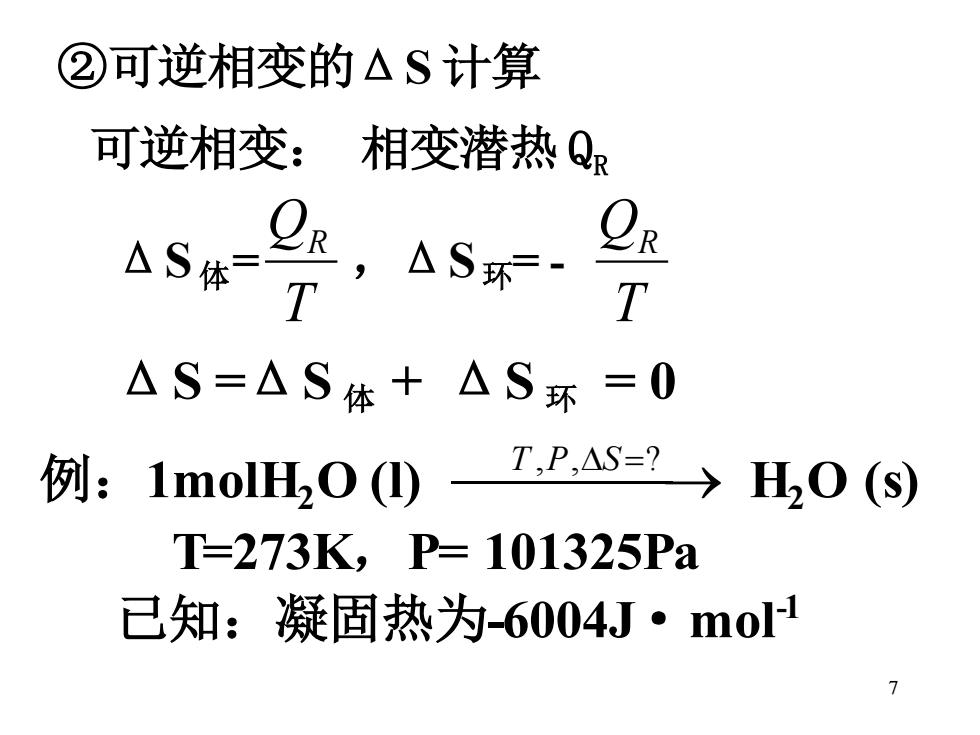
7 ②可逆相变的ΔS 计算 可逆相变: 相变潜热 QR ΔS 体= T QR ,ΔS 环= - T QR ΔS =ΔS 体 + ΔS 环 = 0 例:1molH2 O (l) ⎯T ⎯,P,S ⎯=? → H2 O (s) T=273K,P= 101325Pa 已知:凝固热为-6004J·mol-1

-6004 △S体= =-22J·K T 273 △S环=· 2r=22J·K T △S=△S体+△S环=0 2)不可逆相变化 ①定义:不是发生在两相平衡共存的T,P下 的相变一一不可逆相变 亚(介)稳态的变化:过冷、过热的液体; 过饱和溶液等
8 ΔS 体= T QR = 273 − 6004 = - 22 J·K-1 ΔS 环= - T QR =22 J·K-1 ΔS =ΔS 体 + ΔS 环 = 0 2)不可逆相变化 ①定义:不是发生在两相平衡共存的 T,P 下 的相变——不可逆相变 亚(介)稳态的变化:过冷、过热的液体; 过饱和溶液等

T,P,△S=? 例:1molH2O① >H20(S) T=263K(-10℃),P=P ②不可逆相变的△S计算 需设计可逆过程来计算△S 例:1molH20(① T,P,△S=? →H20(s) T=263K(-10℃),P=P9 273K凝固潜热:-6004J·moH 水的比热:75.3J·K·molH1 冰的比热:36.8J·K1·moH 不可逆过程:QrQR△S≠g 9
9 例:1molH2 O (l) ⎯T ⎯,P,S ⎯=? → H2 O (s) T=263K(-10℃), P=Pθ ②不可逆相变的ΔS 计算 需设计可逆过程来计算ΔS 例:1molH2 O (l) ⎯T ⎯,P,S ⎯=? → H2 O (s) T=263K(-10℃), P=Pθ 273K 凝固潜热:-6004 J·mol-1 水的比热:75.3 J·K-1·mol-1 冰的比热:36.8 J·K-1·mol-1 不可逆过程:QQR T Q S

解:设计可逆过程 263K,p,AS=? H0(0① 7H20(S) 、AS、 △S3 H20(① 273Kp°AS2=”→H20(S) T1=263K,△S= T2=273K,△S2=22J·K1 T? A S1=CP,m (Ln T 273 =75.3Ln =2.8J·K1·mo1 263 10
10 解:设计可逆过程 H2 O (l) ⎯263 ⎯K ⎯,P ⎯,S ⎯=? → H2 O (s) ΔS1 ΔS3 H2 O (l) ⎯273 ⎯K ⎯,P ⎯,S2⎯=? → H2 O (s) T1 =263K,ΔS=? ΔS1 =CP,m(l) Ln 1 2 T T =75.3Ln 263 273 =2.8 J·K-1·mol-1 T2 =273K,ΔS2 =22 J·K -1