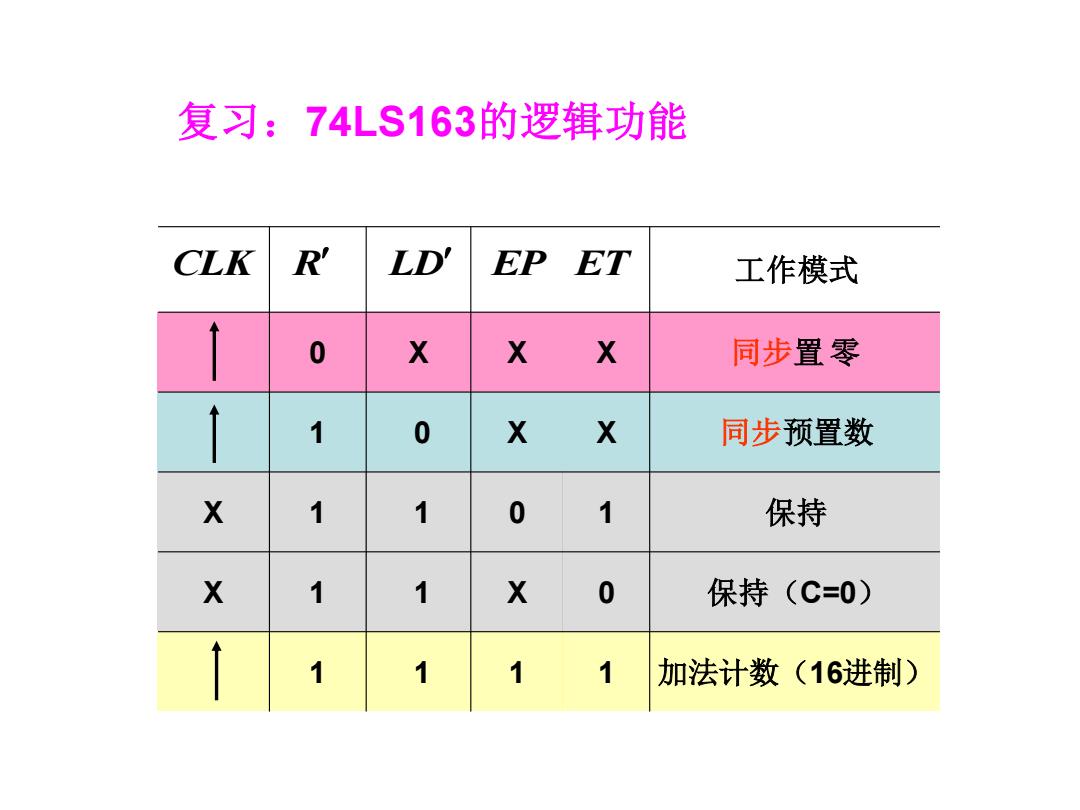
复习:74LS163的逻辑功能 CLK R LD' EP ET 工作模式 0 X X X 同步置零 1 0 X X 同步预置数 X 1 1 0 1 保持 X 1 1 X 0 保持(C=0) 1 加法计数(16进制)
复习:74LS163的逻辑功能 1 1 1 1 加法计数(16进制) X 1 1 X 0 保持(C=0) X 1 1 0 1 保持 1 0 X X 同步预置数 0 X X X 同步置 零 CLK R LD EP ET 工作模式
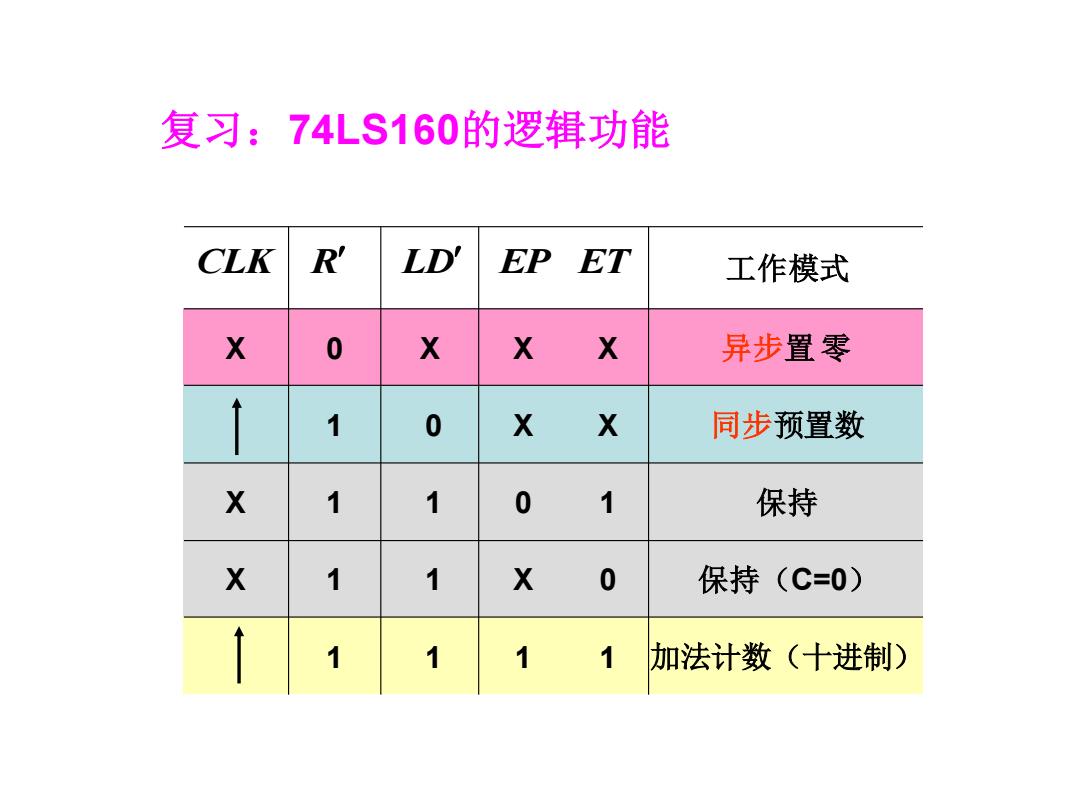
复习:74LS160的逻辑功能 CLK R LD EP ET 工作模式 0 X X 异步置零 1 0 X X 同步预置数 X 1 0 1 保持 X 1 1 X 0 保持(C=0) 加法计数(十进制)
复习:74LS160的逻辑功能 1 1 1 1 加法计数(十进制) X 1 1 X 0 保持(C=0) X 1 1 0 1 保持 1 0 X X 同步预置数 X 0 X X X 异步置 零 CLK R LD EP ET 工作模式

用集成计数器构成任意进制计数器 假设已有N进制计数器,要构成M进制计数器,分两种情况: ◆MN: M=N1xN2g串行进位法、并行进位法 M:矿整体置零法、整体置数法
◆ MN: M=N1N2 串行进位法、并行进位法 M: 整体置零法、整体置数法 用集成计数器构成任意进制计数器 假设已有N进制计数器,要构成M进制计数器,分两种情况:
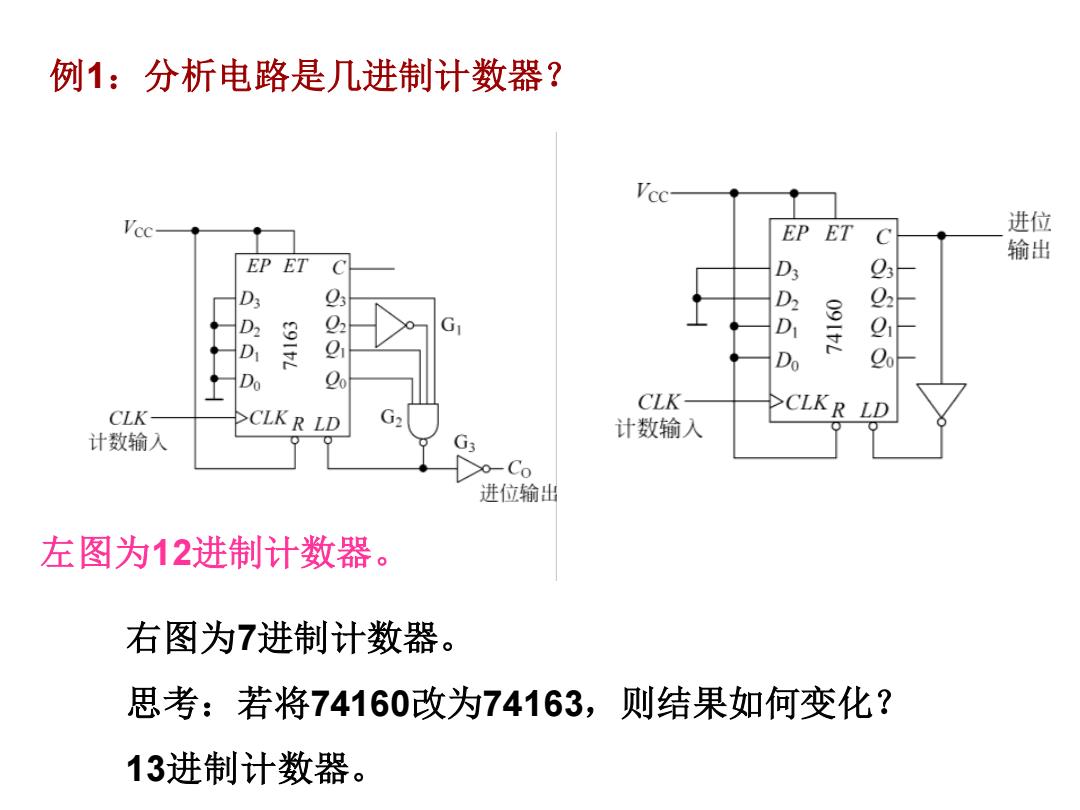
例1:分析电路是几进制计数器? EP ET 进位 C 输出 EP ET D 92 2 02 D D 9 Do CLK- CLK CLK R LD G2 CLKR LD 计数输入 G 计数输入 进位输出 左图为12进制计数器。 右图为7进制计数器。 思考:若将74160改为74163,则结果如何变化? 13进制计数器
例1:分析电路是几进制计数器? 左图为12进制计数器。 右图为7进制计数器。 思考:若将74160改为74163,则结果如何变化? 13进制计数器
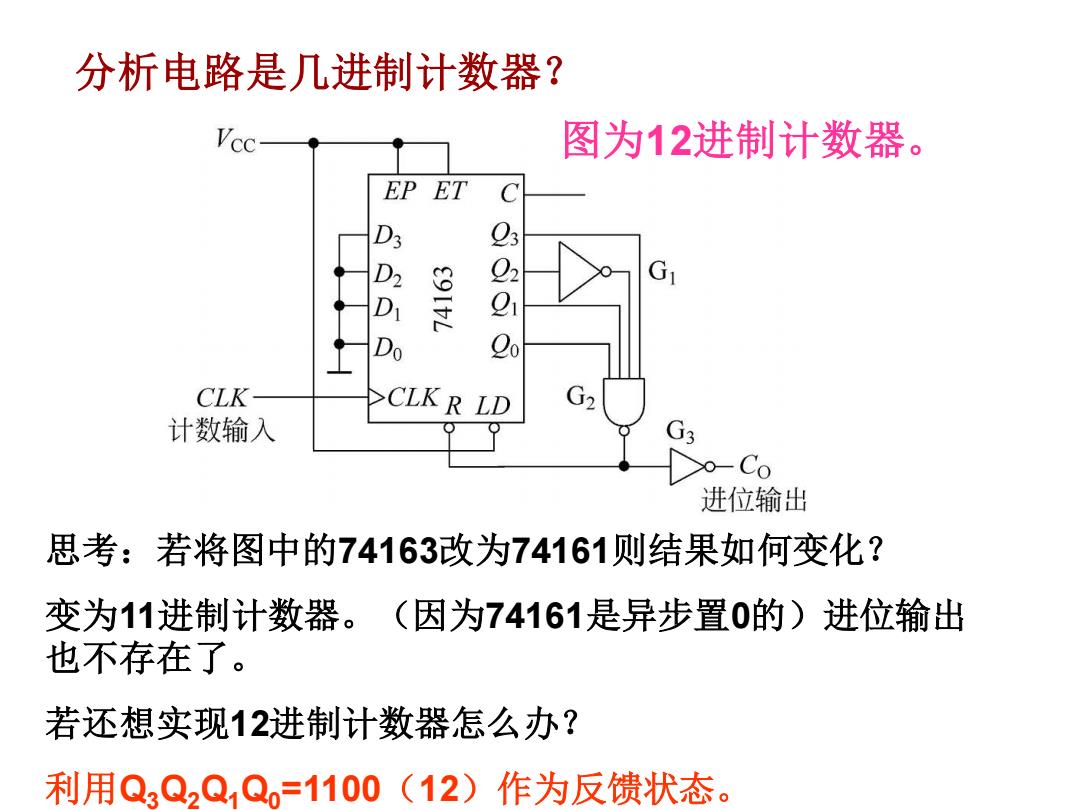
分析电路是几进制计数器? 图为12进制计数器。 EP ET D 23 D E9ItL 92 91 Do 2o CLK -CLK R LD G2 计数输入 G; Xo-Co 进位输出 思考:若将图中的74163改为74161则结果如何变化? 变为11进制计数器。(因为74161是异步置0的)进位输出 也不存在了。 若还想实现12进制计数器怎么办? 利用Q3Q2Q,Q,=1100(12)作为反馈状态
分析电路是几进制计数器? 图为12进制计数器。 思考:若将图中的74163改为74161则结果如何变化? 变为11进制计数器。(因为74161是异步置0的)进位输出 也不存在了。 若还想实现12进制计数器怎么办? 利用Q3Q2Q1Q0=1100(12)作为反馈状态

例2]试利用同步十进制计数器74160接成同步六进制计数器 由于74160是异步清零端 解:反馈置零法 瞬态 0000 000 0010 0110 0101 0100 001 Do D1 D2 D3 EP ET 74160 LD CP- CP 计数输入 Qo Q1 Q2 Q3 0 1 10 N=6 0 Q3Q2Q1Q0=0110
[例2]试利用同步十进制计数器74160接成同步六进制计数器 解: 反馈置零法 0 1 10 0 由于74160是异步清零端 N=6 Q3Q2Q1Q0=0110 0110 0001 0100 0011 0010 0101 0000 瞬态
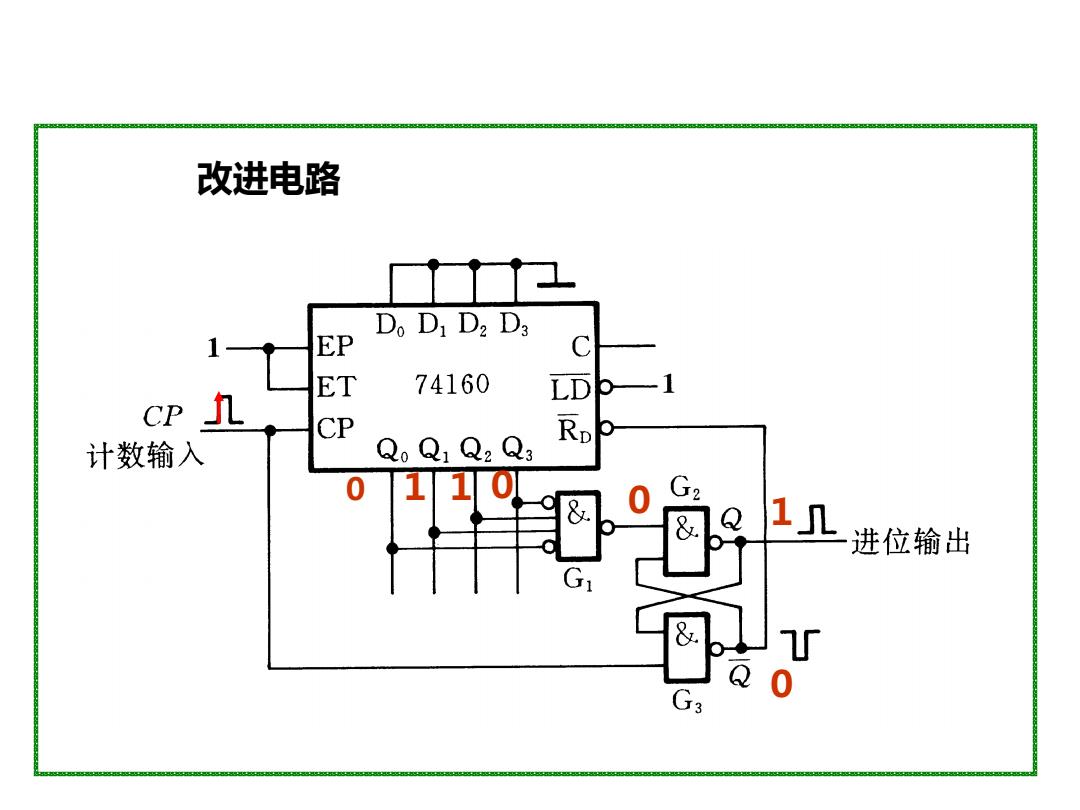
改进电路 Do Di D2 Da 1 EP 九 ET 74160 LD CP CP 计数输入 Qo Q:Q2 Q: RD 110 09 0 G2 98p 进位输出 &
改进电路 0 1 10 0 0 1

[例3]试利用同步十进制计数器74160接成同步六进制计数器 由于74160是同步置数端 解:反馈置数法 置0000,记数范围0~5 0000 000 0010 0101 0100 001 EP Du D:D:D ET 74160 D CP- CP Qo Q:QQ 0 计数 轴入 1010 9& 10
[例3]试利用同步十进制计数器74160接成同步六进制计数器 解: 反馈置数法 1 010 0 置0000,记数范围0~5 由于74160是同步置数端 0001 0100 0011 0010 0101 0000

1001 0000 0001 置1001,记数范围9、0~4 0100 00 001 EP D.D:D:D 74160 CP- CP Rp 计数 Qo Q:Q:Q 临入
置1001,记数范围 9 、0~4 0000 0011 0010 0001 0100 1001
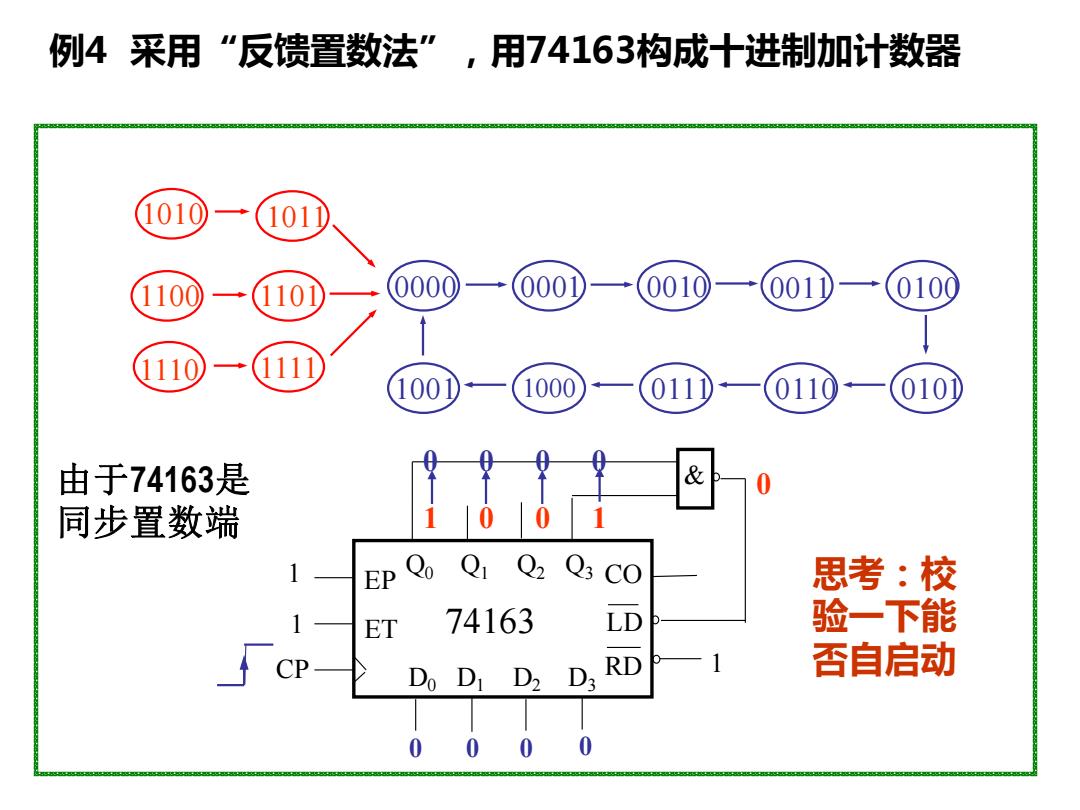
例4采用“反馈置数法”,用74163构成十进制加计数器 1010 101 1100 101 0000 000 0010 001 0100 100 1000 011 0110 010 由于74163是 & 同步置数端 EP Qo Qi Q2 Q3 CO 思考:校 ET 74163 LD 验一下能 CP Do D D2 D3 RD 否自启动 00 00
例4 采用“反馈置数法” ,用74163构成十进制加计数器 0000 0001 0010 0011 0100 1001 1000 0111 0110 0101 1100 1101 1010 1011 1110 1111 & Q0 Q1 Q2 Q3 D0 D1 D2 D3 74163 EP ET CO LD RD 1 1 CP 1 0 0 0 0 1 0 0 1 0 0 0 0 0 思考:校 验一下能 否自启动 由于74163是 同步置数端