
绪论 1.数字电子技术的发展与展望 电子器件的发展历程:电子管时代(20世纪初) →晶体管时代(1950年) →集成电路时代(1960年) IC按集成度分为SSI、MSI、LSI、VLSI →硅片时代(1970年) 片上系统(S0C):把一个复杂的电子系统制作在一个硅片上 2.数字量和模拟量 模拟量:在时间上、数值变化上都是连续的物理量; 模拟信号;模拟电路 数字量:时间上、数值变化上都是离散的物理量; 数字信号;数字电路
绪 论 2.数字量和模拟量 模拟量:在时间上、数值变化上都是连续的物理量; 模拟信号;模拟电路 数字量:时间上、数值变化上都是离散的物理量; 数字信号;数字电路 1.数字电子技术的发展与展望 电子器件的发展历程:电子管时代(20世纪初) →晶体管时代(1950年) → 集成电路时代(1960年) IC按集成度分为SSI、MSI、LSI、VLSI →硅片时代( 1970年) 片上系统(SOC):把一个复杂的电子系统制作在一个硅片上

3.数字电路中0和1的表示方法 数字电路中采用二进制数表示数量的大小,每 一位只有1和0两种状态。 在电路中是用高、低电平分别表示1和0的。 正逻辑:高电平为1、低电平为0 负逻辑:低电平为1、高电平为0 0 注意:高、低电平 允许有一定的变化 0 范围。 正逻辑 负逻辑
3.数字电路中0和1的表示方法 数字电路中采用二进制数表示数量的大小,每 一位只有1和0两种状态。 在电路中是用高、低电平分别表示1和0的。 正逻辑:高电平为1、低电平为0 负逻辑:低电平为1、高电平为0 注意:高、低电平 允许有一定的变化 范围

。产生高、低电平的方法:通过控制半导体 开关电路的开关状态实现。 a 只需一个开关 功耗为0 功率损耗较大 比较理想
• 产生高、低电平的方法:通过控制半导体 开关电路的开关状态实现。 只需一个开关 功率损耗较大 功耗为0 比较理想

4.数字集成电路 按用途分为专用型和通用型。 专用型数字集成电路是为某种特定用途而专门设计、制造的。 通用型数字集成电路产品中又有两种类型:一种是逻辑功能固定 的标准化、系列化产品;另一种是可编程逻辑器件(PLD) 。 PLD的内部包含了大量的基本逻辑单元电路,通过写入编程数据, 可以将这些单元连接成所需要的逻辑电路。因此,它的产品是通用型 的,而它所实现的逻辑功能则由用户根据自己的需要通过编程来设定。 5.EDA技术的发展与应用 电子设计自动化(EDA)是将计算机技术应用于电子电路设计过程 而产生的一门新技术。它广泛地应用于电路结构设计和运行状态的仿真、 集成电路版图的设计、印刷电路板的设计以及可编程逻辑器件的编程设 计等所有设计环节当中。 常用仿真软件有:Multisim、Proteus等 硬件描述语言:VHDL、Verilog HDL
4.数字集成电路 按用途分为专用型和通用型。 专用型数字集成电路是为某种特定用途而专门设计、制造的。 通用型数字集成电路产品中又有两种类型:一种是逻辑功能固定 的标准化、系列化产品;另一种是可编程逻辑器件(PLD)。 PLD的内部包含了大量的基本逻辑单元电路,通过写入编程数据, 可以将这些单元连接成所需要的逻辑电路。因此,它的产品是通用型 的,而它所实现的逻辑功能则由用户根据自己的需要通过编程来设定。 5.EDA技术的发展与应用 常用仿真软件有:Multisim、Proteus等 硬件描述语言:VHDL、Verilog HDL 电子设计自动化(EDA)是将计算机技术应用于电子电路设计过程 而产生的一门新技术。它广泛地应用于电路结构设计和运行状态的仿真、 集成电路版图的设计、印刷电路板的设计以及可编程逻辑器件的编程设 计等所有设计环节当中
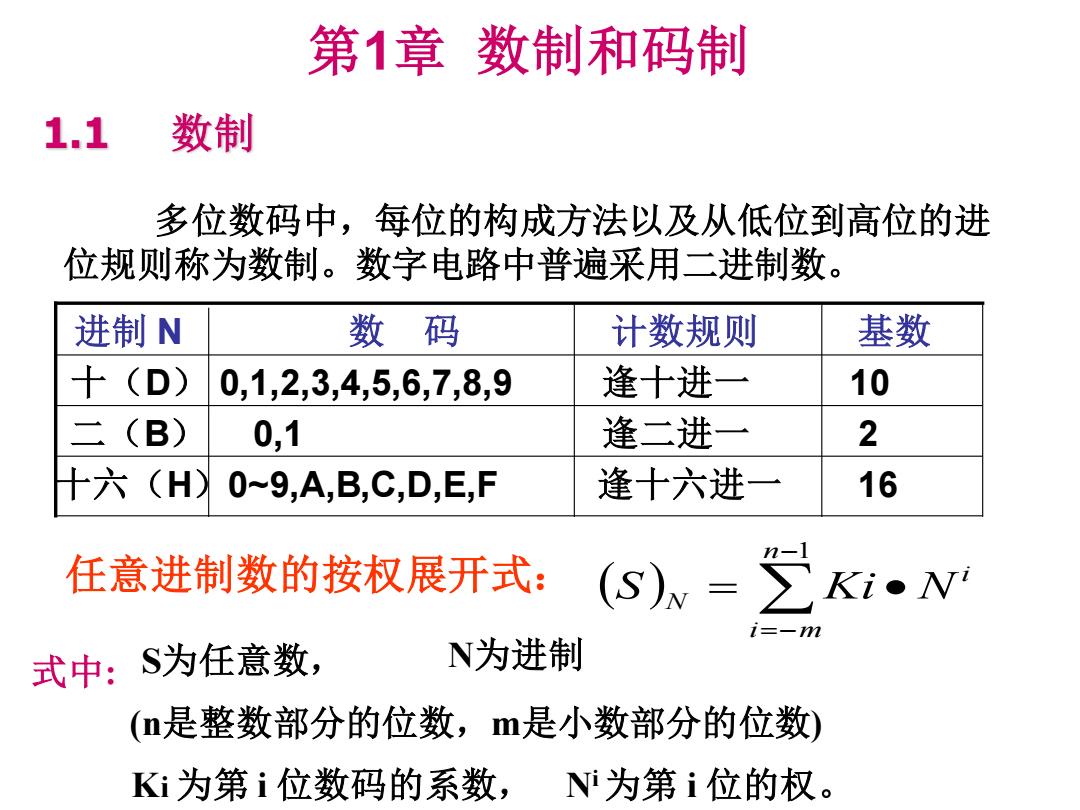
第1章数制和码制 1.1 数制 多位数码中,每位的构成方法以及从低位到高位的进 位规则称为数制。数字电路中普遍采用二进制数。 进制N 数 码 计数规则 基数 十(D) 0,1,2,3,4,5,6,7,8,9 逢十进一 10 二(B) 0,1 逢二进一 2 十六(H) 0~9,A,B,C,D,E,F 逢十六进一 16 任意进制数的按权展开式: (S)= 式中: S为任意数, N为进制 (n是整数部分的位数,m是小数部分的位数) Ki为第i位数码的系数,Ni为第i位的权
第1章 数制和码制 多位数码中,每位的构成方法以及从低位到高位的进 位规则称为数制。数字电路中普遍采用二进制数。 (n是整数部分的位数,m是小数部分的位数) 二(B) 0,1 逢二进一 2 十(D) 0,1,2,3,4,5,6,7,8,9 逢十进一 10 进制 N 数 码 计数规则 基数 ( ) − =− = • n 1 i m i S N Ki N 1.1 数制 任意进制数的按权展开式: 式中: S为任意数, N为进制 Ki 为第 i 位数码的系数, Ni 为第 i 位的权。 十六(H)0~9,A,B,C,D,E,F 逢十六进一 16

1.几种常用的数制 几种进荆数之间的对应关系 十进制数 二进制数 八进制数 十六进制数 0 00000 0 0 00001 1 1 00010 2 2 3 00011 3 4 00100 4 4 5 00101 5 5 6 00110 6 6 7 00111 7 7 8 01000 10 8 9 01001 11 9 10 01010 12 11 01011 13 B 12 01100 14 13 01101 15 D 14 01110 16 E 15 01111 17 F
1. 几种常用的数制 几种进制数之间的对应关系 十进制数 二进制数 八进制数 十六进制数 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 00000 00001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 0 1 2 3 4 5 6 7 8 9 A B C D E F

2、不同数制间的转换 1) 二→十 其它进制数转换为十进制数,用“按权展开,相加即可”。 例: (1011)2=1×23+0×22+1×21+1×20 =8+0+2+1=(11)10 将代码为1的数权值相加,即得对应的十进制数。 2)十→二 十进制转换成其它进制: 整数部分用“除N取余,逆序排列法”。 小数部分用“乘取整,顺序排列法”。 例:将(123.6875)10转换成二进制数。 (123.6875)10=(1111011.1011)2
2 、 不同数制间的转换 1) 二→ 十 2 ) 十 → 二 其它进制数转换为十进制数,用“按权展开,相加即可”。 整数部分用“除N取余,逆序排列法”。 例: (1011)2 + 0×2 2 + 1×2 1 + 1×2 0 =1×2 3 十进制转换成其它进制: = 8 + 0 + 2 + 1 =(11)10 将代码为1 的数权值相加,即得对应的十进制数。 小数部分用 “乘N取整,顺序排列法”。 例:将(123.6875)10转换成二进制数。 (123.6875)10=(1111011.1011)2
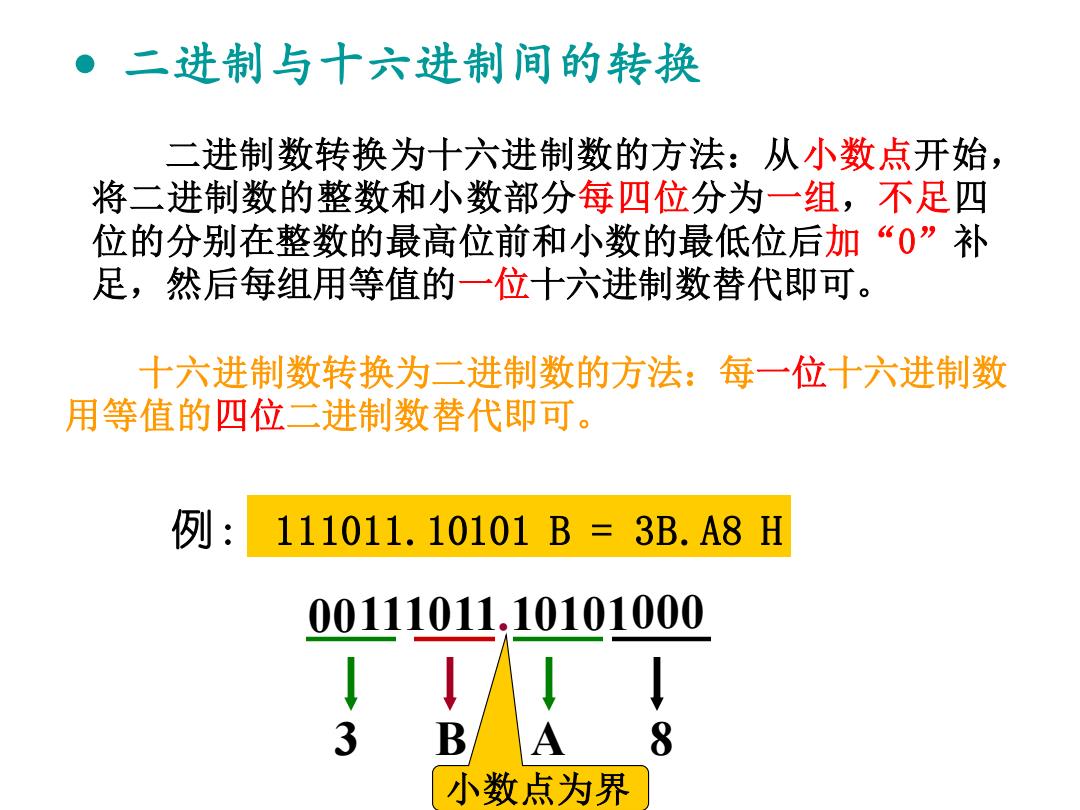
二进制与十六进制间的转换 二进制数转换为十六进制数的方法:从小数点开始, 将二进制数的整数和小数部分每四位分为一组,不足四 位的分别在整数的最高位前和小数的最低位后加“0”补 足,然后每组用等值的一位十六进制数替代即可。 十六进制数转换为二进制数的方法:每一位十六进制数 用等值的四位二进制数替代即可。 例: 111011.10101B=3B.A8H 00111011.10101000 3】 小数点为界
小数点为界 • 二进制与十六进制间的转换 二进制数转换为十六进制数的方法:从小数点开始, 将二进制数的整数和小数部分每四位分为一组,不足四 位的分别在整数的最高位前和小数的最低位后加“0”补 足,然后每组用等值的一位十六进制数替代即可。 例: 111011.10101 B = 3B.A8 H 111011.10101 B = ? H 00111011.10101000 3 B A 8 十六进制数转换为二进制数的方法:每一位十六进制数 用等值的四位二进制数替代即可

思考:十进制与十六进制间如何转换? (3D.8)16=(61.5)10 (138.25)10=(8A.4 16
思考:十进制与十六进制间如何转换? (3D.8)16=( )10 (138.25)10=( )16 61.5 8A.4

1.2编码 不同的数码不仅可以表示数量的大小,还可以表 示不同的事物。用来表示不同事物的数码称为代码。 编制代码遵循的规则叫做“码制”。 1、二十进制码(BCD码): 用四位二进制数码表示一位十进制数码的计数方法。 BCD代码有多种不同的码制: 8421BCD码、2421BCD码、 余3码等 内容见下表
1.2 编码 内容见下表 用四位二进制数码表示一位十进制数码的计数方法。 不同的数码不仅可以表示数量的大小,还可以表 示不同的事物。用来表示不同事物的数码称为代码。 编制代码遵循的规则叫做“码制”。 BCD代码有多种不同的码制: 8421BCD 码、 2421BCD码、 余3码等 1、二-十进制码(BCD码):