2.3.7逻辑函数描述方法间的转换 1逻辑函数式与真值表之间的转换 A B C F 0 0 0 0 0 0 1 0 ()、由真值表写出逻辑函数式 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 输入变量取值为1用原变量表 逻辑函数式: 示;反之,则用反变量表示 ·挑出函数值为1的输入组A'BC.AB'C、ABC ·写出函数值为1的输入组合对应的乘积项 •将这些乘积项相加就得到逻辑表达式 F =A'BC+AB'C+ABC
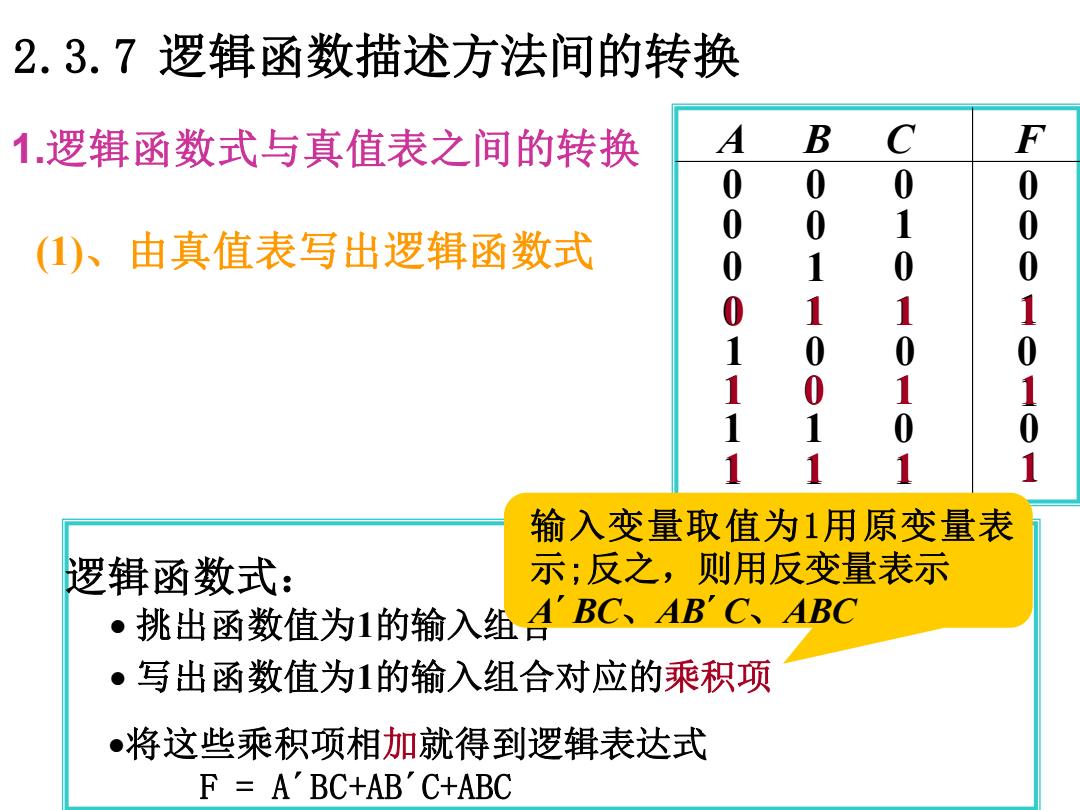
逻辑函数式: • 挑出函数值为1的输入组合 1 0 1 0 0 1 1 0 0 0 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 A B C F 0 0 1 0 1 1 1 1 0 1 1 1 1 1 1 • 写出函数值为1的输入组合对应的乘积项 •将这些乘积项相加就得到逻辑表达式 F = A´BC+AB´C+ABC 输入变量取值为1用原变量表 示;反之,则用反变量表示 A´BC、AB´C、ABC 2.3.7 逻辑函数描述方法间的转换 (1)、由真值表写出逻辑函数式 1.逻辑函数式与真值表之间的转换
(2)、由逻辑函数式写出真值表 将输入变量取值的所有组合状态(n个输 入变量共有2"种组合)逐一代入逻辑式求出函 数值,列成表即可。 例题:已知逻辑函数Y=A+B'C+A'BC',求它对应的真值表。 A B C 0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 7 0 1 1 1 0 1 A 1
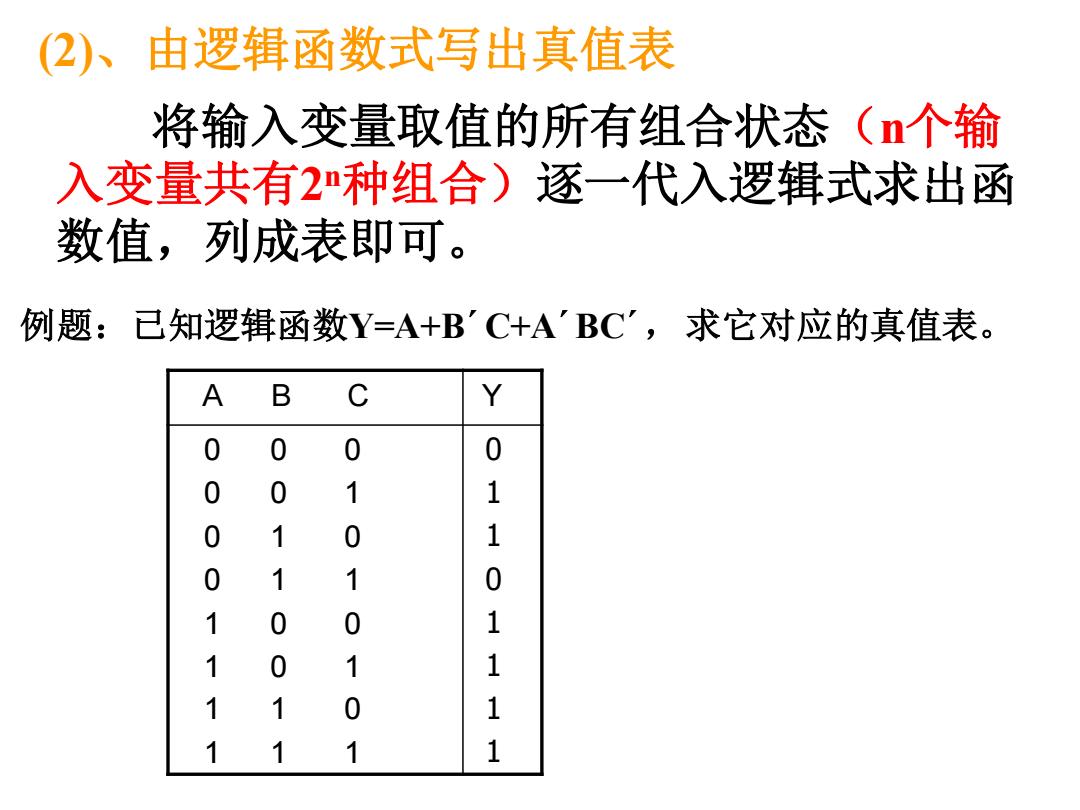
例题:已知逻辑函数Y=A+B´C+A´BC´ ,求它对应的真值表。 A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 (2)、由逻辑函数式写出真值表 将输入变量取值的所有组合状态(n个输 入变量共有2 n种组合)逐一代入逻辑式求出函 数值,列成表即可
2、逻辑函数式与逻辑图之间的转换 (1)、由逻辑函数式画出逻辑图 用逻辑符号代替逻辑式中的运算符号即可。 例题:已知逻辑函数为Y=(AB)'+BC)',画出逻辑图。 A B
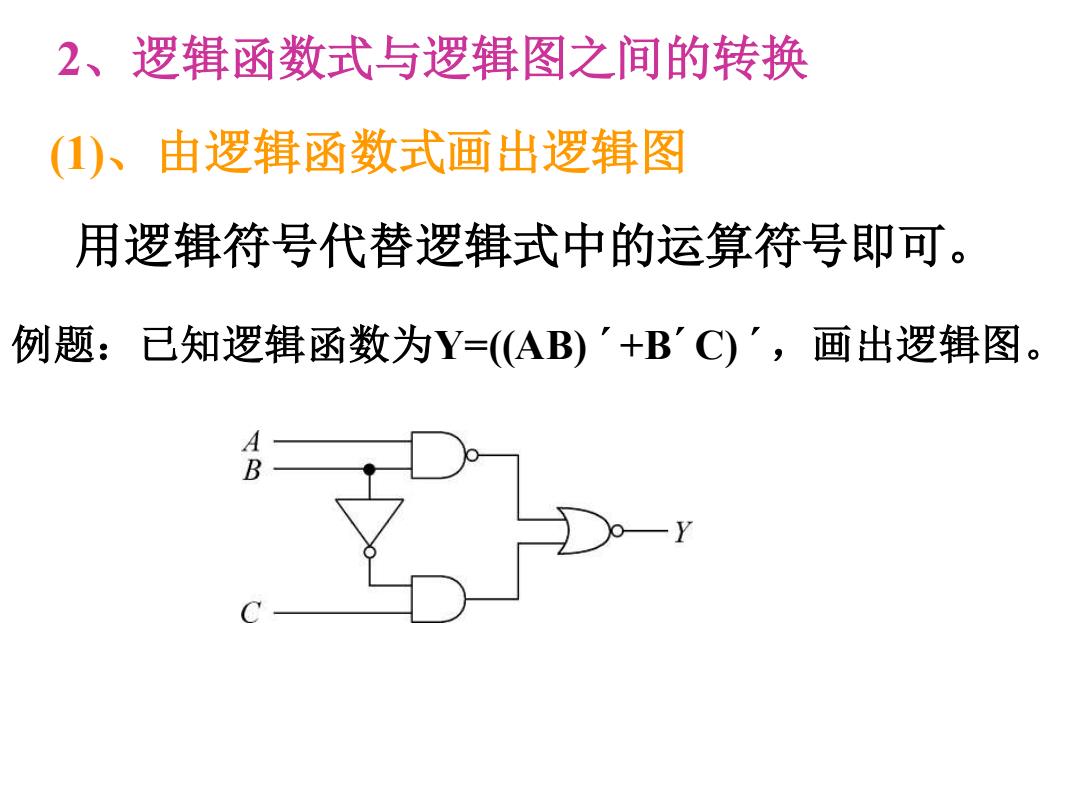
例题:已知逻辑函数为Y=((AB) ´+B´C) ´,画出逻辑图。 (1)、由逻辑函数式画出逻辑图 用逻辑符号代替逻辑式中的运算符号即可。 2、逻辑函数式与逻辑图之间的转换
(2)、由逻辑图写出逻辑函数式 从输入端到输出端逐级写出每个逻辑符号对 应的逻辑式即可。 例题:已知逻辑图如下,请写出逻辑式 4'CD p—Y=(A'B+A'CD+BD) BD
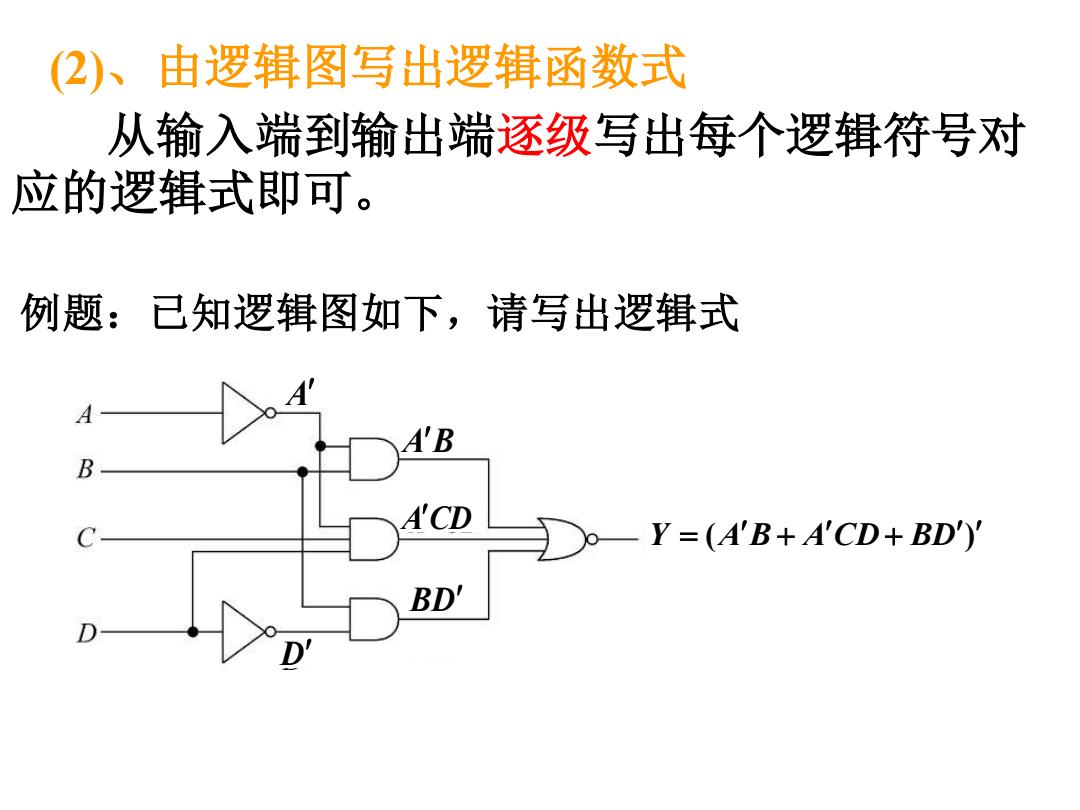
Y = (AB + ACD + BD) BD A ACD AB D 从输入端到输出端逐级写出每个逻辑符号对 应的逻辑式即可。 例题:已知逻辑图如下,请写出逻辑式 (2)、由逻辑图写出逻辑函数式
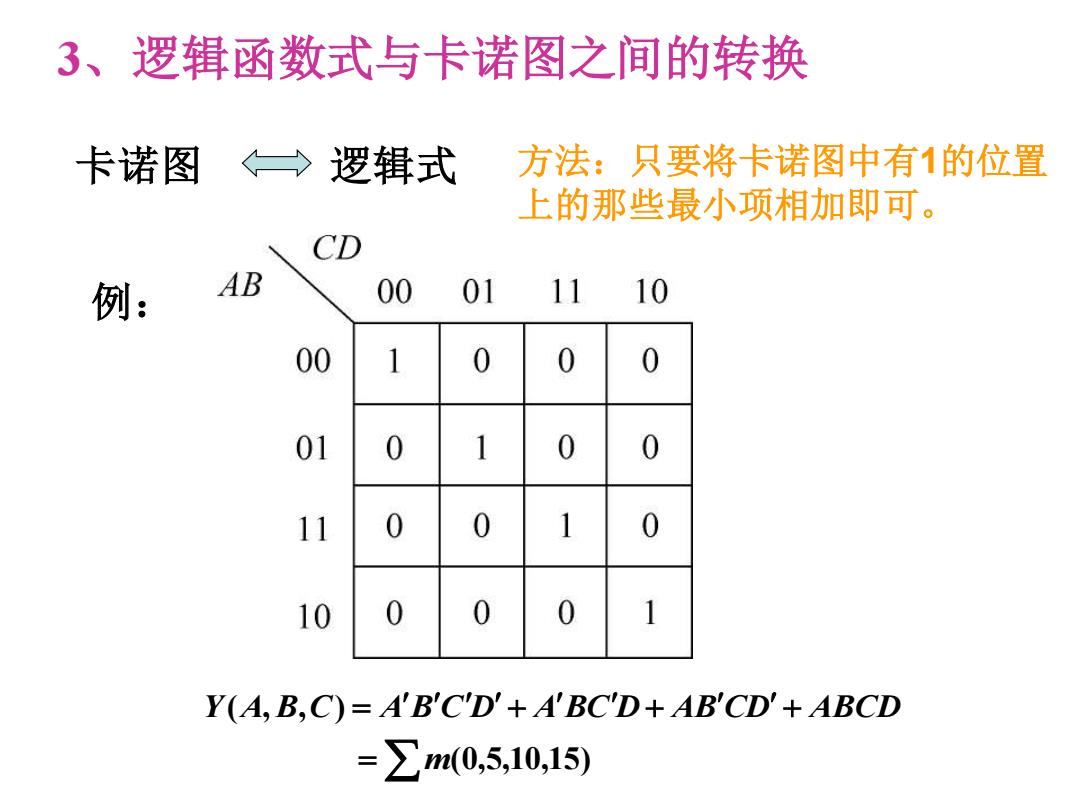
3、逻辑函数式与卡诺图之间的转换 卡诺图。 →逻辑式 方法:只要将卡诺图中有1的位置 上的那些最小项相加即可。 CD 例: AB 00 01 11 10 00 01 11 0 0 0 10 Y(A,B,C)=A'B'C'D'+A'BC'D+AB'CD'+ABCD =∑m(0,5,10,15)
3、逻辑函数式与卡诺图之间的转换 卡诺图 逻辑式 方法:只要将卡诺图中有1的位置 上的那些最小项相加即可。 = = + + + (0,5,10,15) ( , , ) m Y A B C A B C D A BC D AB CD ABCD 例:
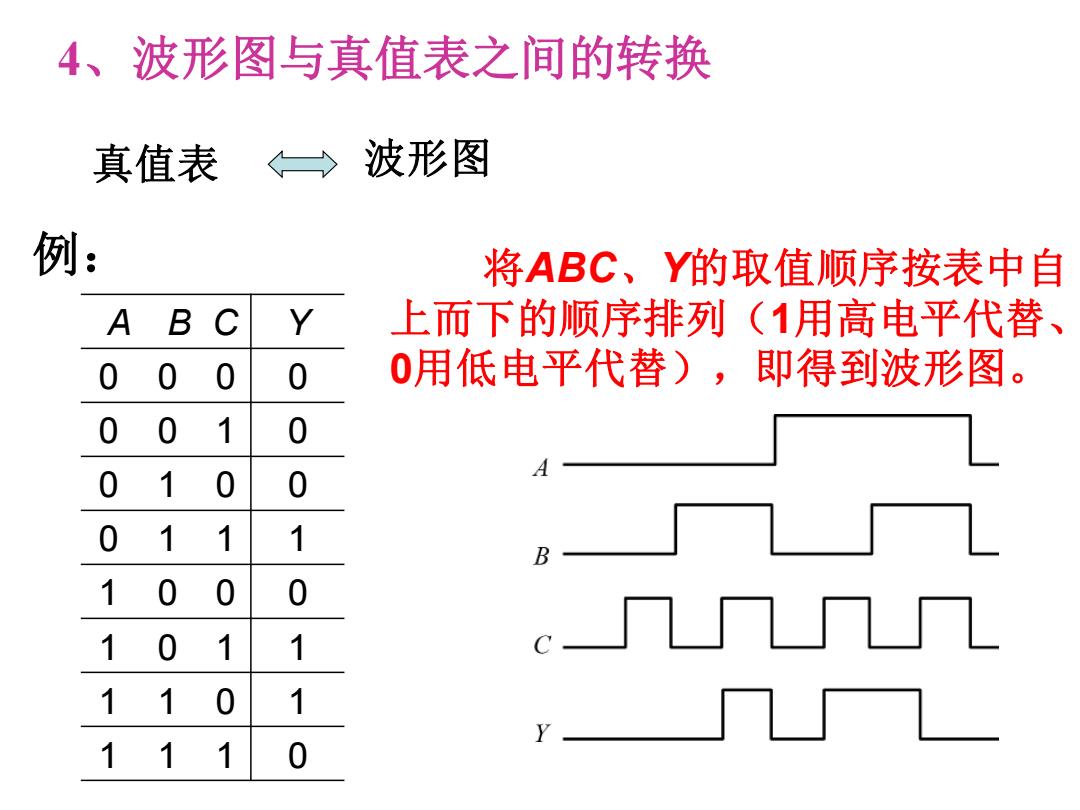
4、波形图与真值表之间的转换 真值表、 →波形图 例: 将ABC、Y的取值顺序按表中自 A BC 上而下的顺序排列(1用高电平代替、 0 0 0 0 0用低电平代替),即得到波形图。 0 0 1 0 0 1 0 0 1 1 1 1 0 0 0 1 01 1 1 1 0 1 11 0
A B C Y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 0 真值表 波形图 将ABC、Y的取值顺序按表中自 上而下的顺序排列(1用高电平代替、 0用低电平代替),即得到波形图。 例: 4、波形图与真值表之间的转换
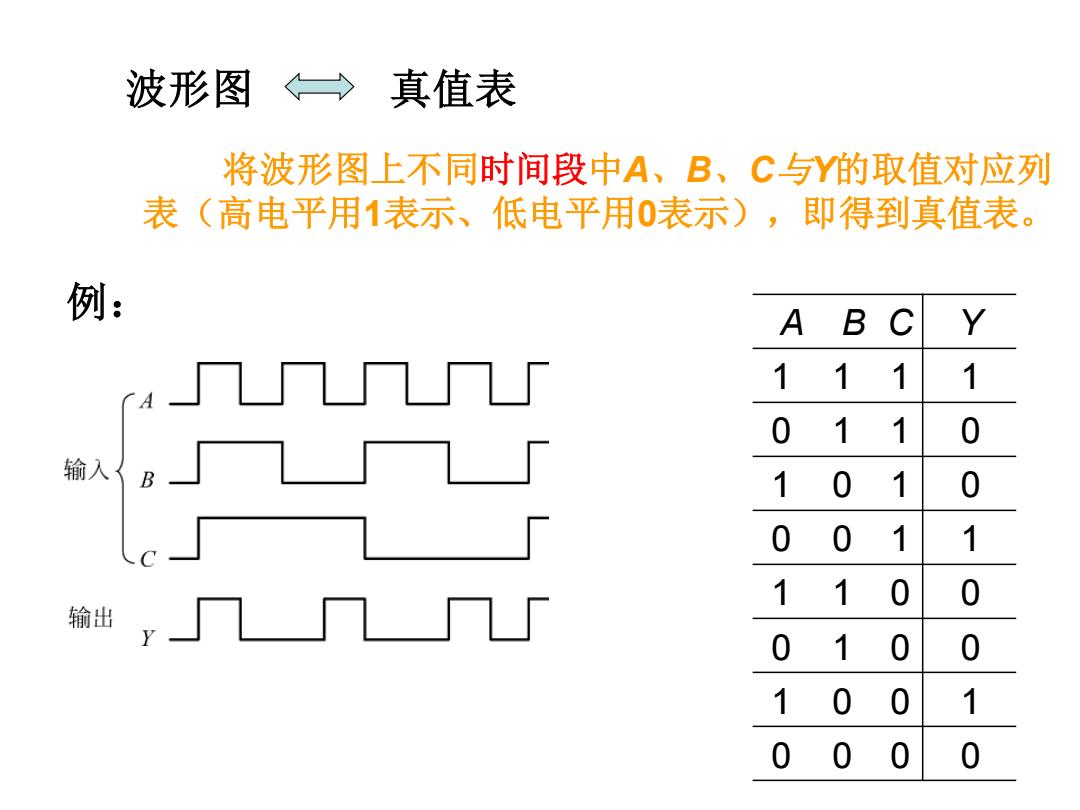
波形图 真值表 将波形图上不同时间段中A、B、C与Y的取值对应列 表(高电平用1表示、低电平用0表示),即得到真值表。 例: A BC 1 1 0 11 0 输入 1 01 0 0 0 1 1 1 0 0 输出 0 1 0 0 0 0 1 0 0 0 0
A B C Y 1 1 1 1 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 波形图 真值表 例: 将波形图上不同时间段中A、B、C与Y的取值对应列 表(高电平用1表示、低电平用0表示),即得到真值表
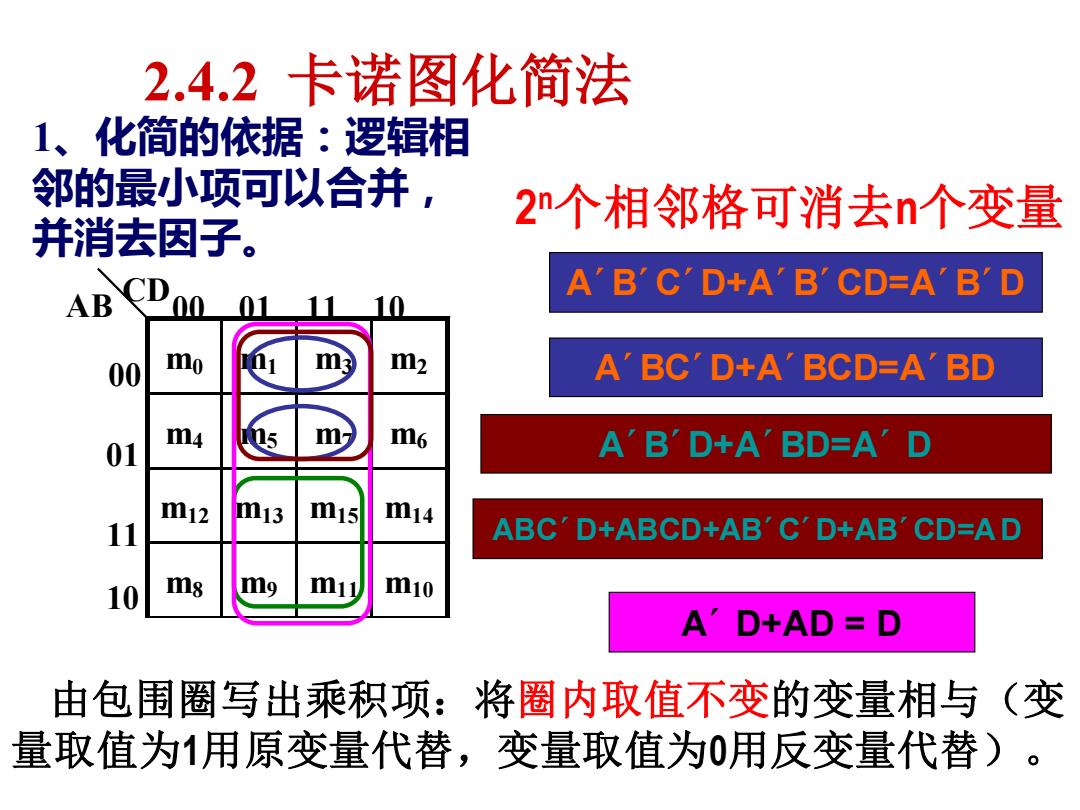
2.4.2卡诺图化简法 1、化简的依据:逻辑相 邻的最小项可以合并, 2n个相邻格可消去n个变量 并消去因子。 A'B'C'D+A'B'CD=A'B'D AB CD 00 mo m2 A'BC'D+A'BCD=A BD m6 01 m4 A B'D+A'BD=A'D m12 113 m15 m14 11 ABC'D+ABCD+AB'C'D+AB'CD=AD 10 ms m10 A'D+AD=D 由包围圈写出乘积项:将圈内取值不变的变量相与(变 量取值为1用原变量代替,变量取值为0用反变量代替)
2.4.2 卡诺图化简法 1、化简的依据:逻辑相 邻的最小项可以合并, 并消去因子。 m0 m1 m3 m2 m4 m5 m7 m6 m12 m13 m15 m14 m8 m9 m11 m10 AB CD00 01 11 10 00 01 11 10 2 n个相邻格可消去n个变量 由包围圈写出乘积项:将圈内取值不变的变量相与(变 量取值为1用原变量代替,变量取值为0用反变量代替)。 A´B´C´D+A´B´CD=A´B´D A´BC´D+A´BCD=A´BD ABC´D+ABCD+AB´C´D+AB´CD=A D A´B´D+A´BD=A´ D A´ D+AD = D

2、化简的步骤 用卡诺图化简逻辑函数的步骤如下: (1)将逻辑函数写成最小项表达式 (2)按最小项表达式填卡诺图,凡式中包含了的最小项, 其对应方格填1,其余方格填0(或不填)。 (3)合并最小项,即将相邻的1方格圈成一组(画一个包围 圈),每一组含2个方格,对应每个包围圈写成一个新的 乘积项。 (4)将所有包围圈对应的乘积项相加。 特别注意:卡诺图中所有的1都必须圈到, 不能合并的1必须单独画圈
2、化简的步骤 用卡诺图化简逻辑函数的步骤如下: (4) 将所有包围圈对应的乘积项相加。 (1) 将逻辑函数写成最小项表达式 (2) 按最小项表达式填卡诺图,凡式中包含了的最小项, 其对应方格填1,其余方格填0(或不填)。 (3) 合并最小项,即将相邻的1方格圈成一组(画一个包围 圈),每一组含2 n个方格,对应每个包围圈写成一个新的 乘积项。 特别注意:卡诺图中所有的 1 都必须圈到, 不能合并的1 必须单独画圈
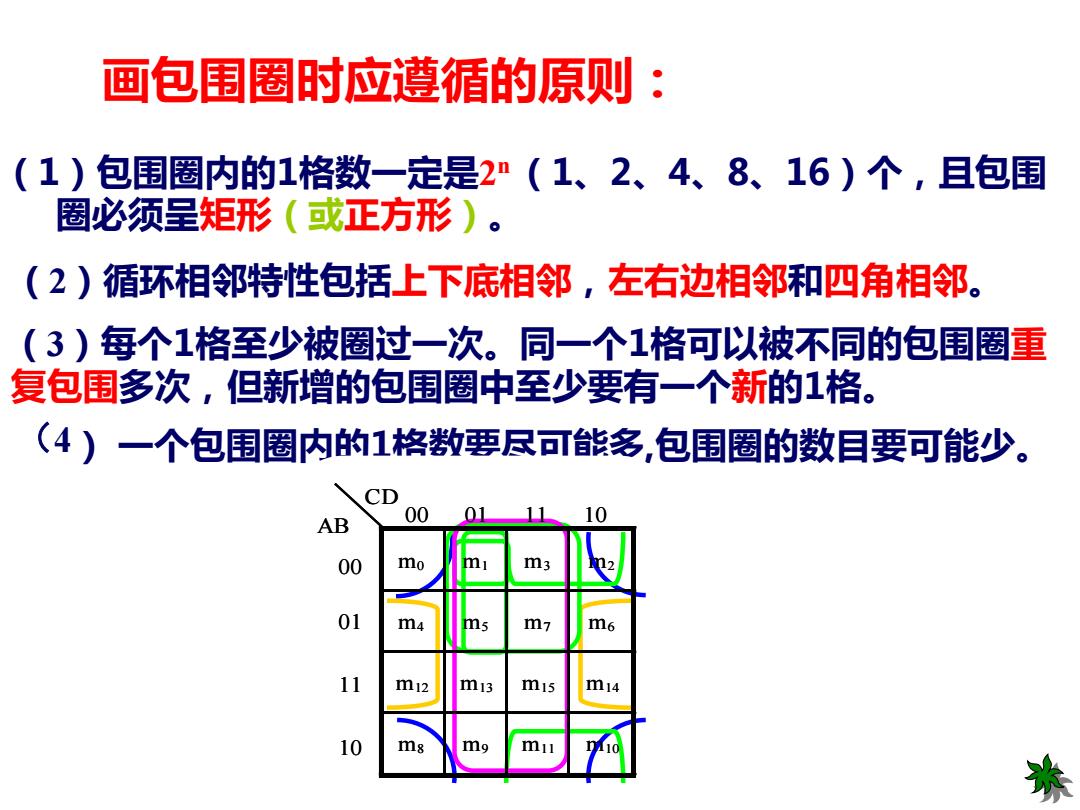
画包围圈时应遵循的原则: (1)包围圈内的1格数一定是2n(1、2、4、8、16)个,且包围 圈必须呈矩形(或正方形)。 (2)循环相邻特性包括上下底相邻,左右边相邻和四角相邻。 (3)每个1格至少被圈过一次。同一个1格可以被不同的包围圈重 复包围多次,但新增的包围圈中至少要有一个新的1格。 (4)一个包围圈内的1格数要尽可能名,包围圈的数目要可能少。 CD AB 00 01 10 00 mo m m m7 m6 m12 m13 m15 m14 10 ms m11
画包围圈时应遵循的原则: (1)包围圈内的1格数一定是2 n (1、2、4、8、16)个,且包围 圈必须呈矩形(或正方形)。 (2)循环相邻特性包括上下底相邻,左右边相邻和四角相邻。 (3)每个1格至少被圈过一次。同一个1格可以被不同的包围圈重 复包围多次,但新增的包围圈中至少要有一个新的1格。 (4) 一个包围圈内的1格数要尽可能多,包围圈的数目要可能少。 m0 m1 m3 m2 m4 m5 m7 m6 m12 m13 m15 m14 m8 m9 m11 m10 00 01 11 10 AB CD 00 01 11 10 m0 m1 m3 m2 m4 m5 m7 m6 m12 m13 m15 m14 m8 m9 m11 m10 00 01 11 10 AB CD 00 01 11 10