
第2章逻辑代数及其应用 用不同的数字可以表示不同数量的大小,也可以表示不 同的事物或同一事物的不同状态。 逻辑状态:用数字1、0表示事物的状态。 所谓“逻辑”是指事物的因果关系。按照事物之间存 在的因果关系进行推理运算逻辑运算。 1849年英国的数学家乔治.布尔首先提出了进行逻辑运算的 数学方法--逻辑代数→开关代数→布尔代数。 逻辑代数已成为分析和设计数字逻辑电路的主要数学工具。 ©参与逻辑运算的变量叫逻辑变量,用大写英文字母(A, B.…)表示。每个变量的取值只有0、1两种。0、1不表 示数的大小,而是代表两种对立的逻辑状态
1849年英国的数学家乔治.布尔首先提出了进行逻辑运算的 数学方法----逻辑代数→开关代数→布尔代数。 逻辑代数已成为分析和设计数字逻辑电路的主要数学工具。 参与逻辑运算的变量叫逻辑变量,用大写英文字母(A, B……)表示。每个变量的取值只有0 、1两种。 0、1不表 示数的大小,而是代表两种对立的逻辑状态。 第2章 逻辑代数及其应用 所谓“逻辑”是指事物的因果关系。按照事物之间存 在的因果关系进行推理运算--逻辑运算。 用不同的数字可以表示不同数量的大小,也可以表示不 同的事物或同一事物的不同状态。 逻辑状态:用数字1、0表示事物的状态
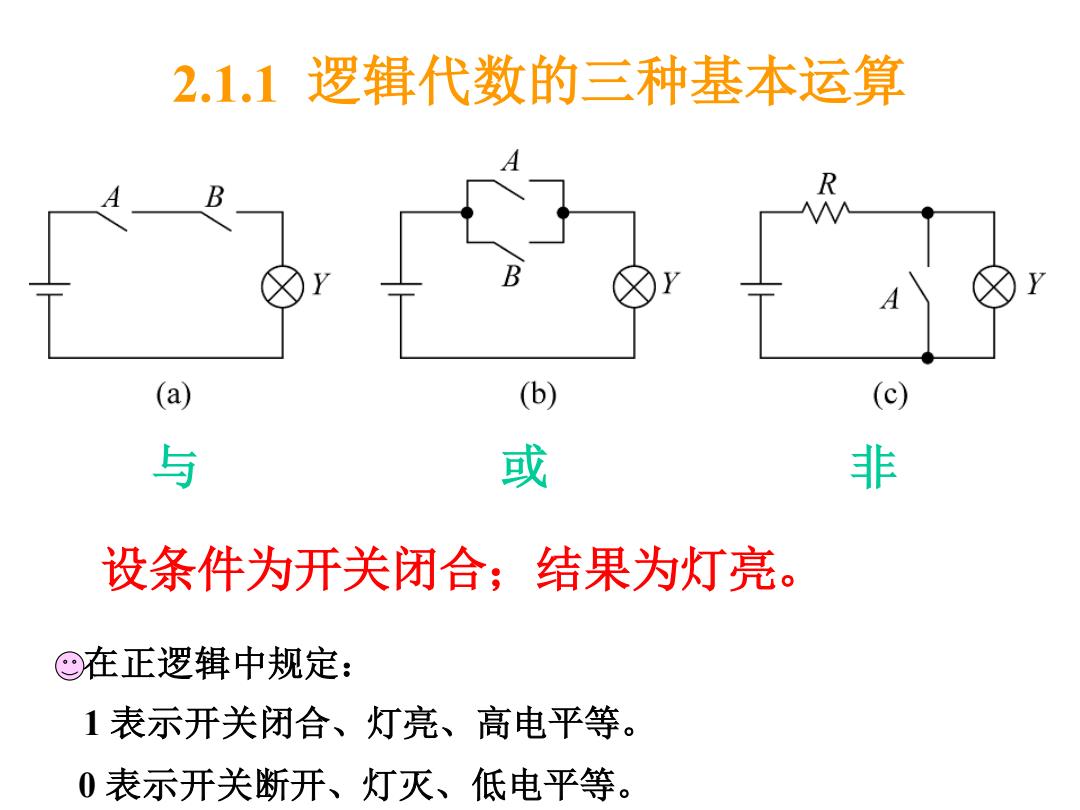
2.1.1逻辑代数的三种基本运算 (a) (b) (c) 与 或 非 设条件为开关闭合;结果为灯亮。 ©在正逻辑中规定: 1表示开关闭合、灯亮、高电平等。 0表示开关断开、灯灭、低电平等
设条件为开关闭合;结果为灯亮。 2.1.1 逻辑代数的三种基本运算 在正逻辑中规定: 1 表示开关闭合、灯亮、高电平等。 0 表示开关断开、灯灭、低电平等。 与 或 非
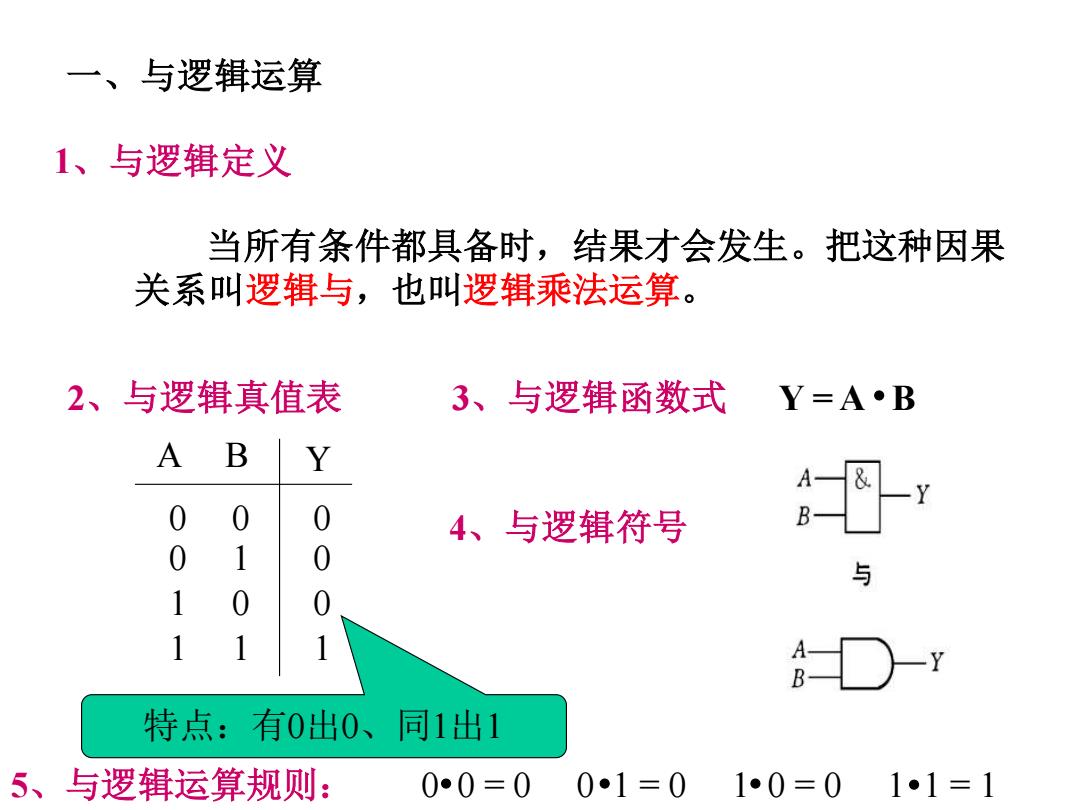
一、与逻辑运算 1、与逻辑定义 当所有条件都具备时,结果才会发生。把这种因果 关系叫逻辑与,也叫逻辑乘法运算。 2、与逻辑真值表 3、与逻辑函数式 Y=A·B A B Y 0 0 4、与逻辑符号 0 1 0 与 1 1 特点:有0出0、同1出1 5、与逻辑运算规则: 0●0=00•1=01•0=0 1•1=1
2、与逻辑真值表 3、与逻辑函数式 4、与逻辑符号 5、与逻辑运算规则: 0 0 = 0 0 1 = 0 1 0 = 0 1 1 = 1 Y = A B A B Y 0 0 0 1 1 0 1 1 0 0 0 1 一、与逻辑运算 1、与逻辑定义 当所有条件都具备时,结果才会发生。把这种因果 关系叫逻辑与,也叫逻辑乘法运算。 特点:有0出0、同1出1
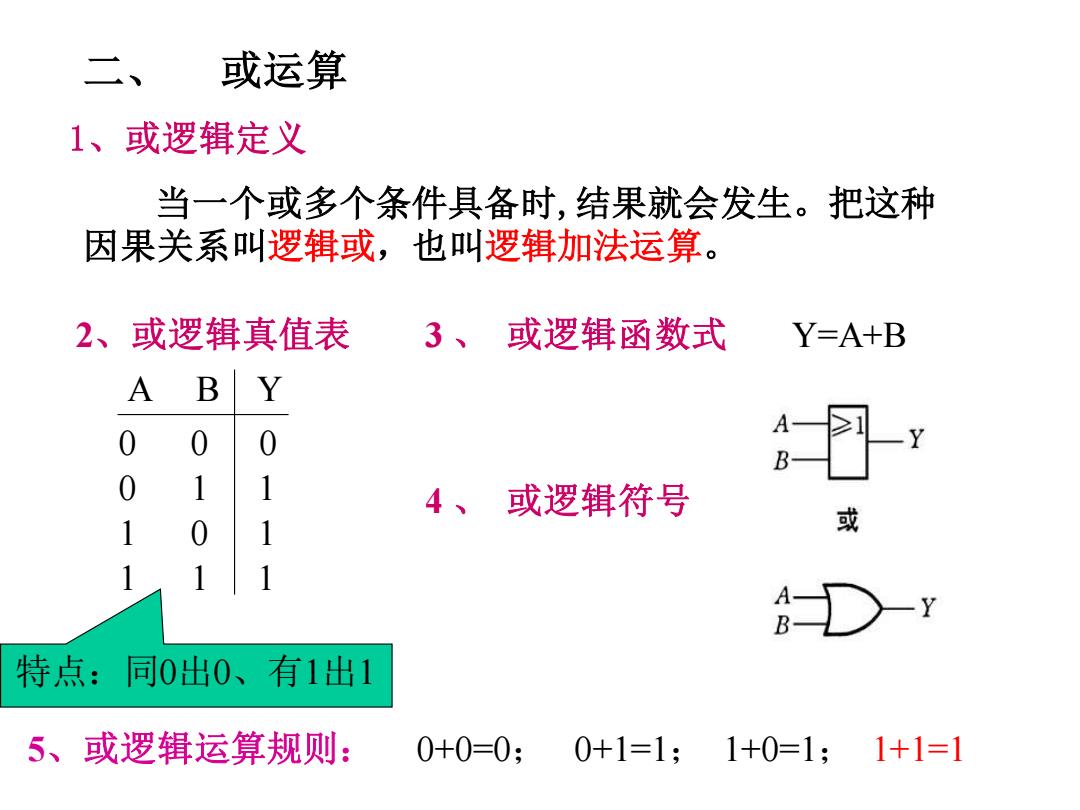
二y 或运算 1、或逻辑定义 当一个或多个条件具备时,结果就会发生。把这种 因果关系叫逻辑或,也叫逻辑加法运算。 2、或逻辑真值表 3、或逻辑函数式 Y=A+B A BY 0 0 0 0 1 1 4、或逻辑符号 1 0 或 8D-Y 特点:同0出0、有1出1 5、或逻辑运算规则: 0+0=0; 0+1=1;1+0=1;1+1=1
二、 或运算 当一个或多个条件具备时,结果就会发生。把这种 因果关系叫逻辑或,也叫逻辑加法运算。 A B 0 1 1 0 1 1 Y 0 1 1 1 2、或逻辑真值表 3 、 或逻辑函数式 4 、 或逻辑符号 Y=A+B 5、或逻辑运算规则: 0+0=0; 0+1=1; 1+0=1; 1+1=1 1、或逻辑定义 0 0 特点:同0出0、有1出1
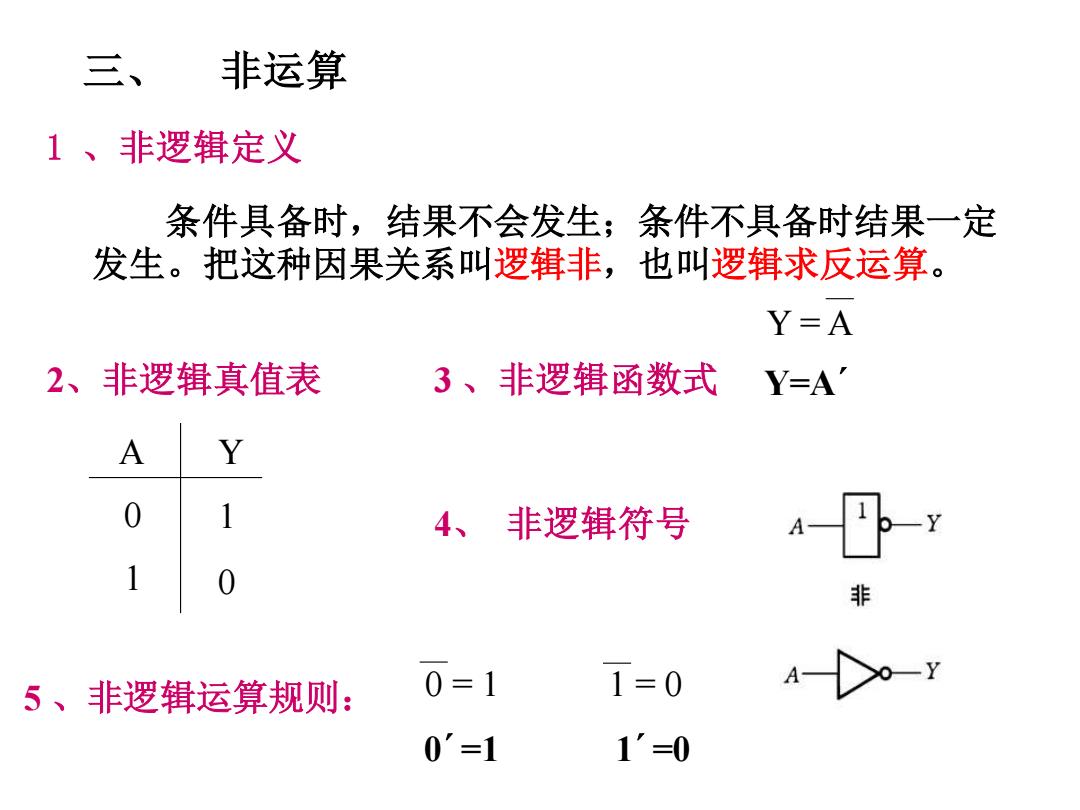
三、 非运算 1、非逻辑定义 条件具备时,结果不会发生;条件不具备时结果一定 发生。把这种因果关系叫逻辑非,也叫逻辑求反运算。 Y=A 2、非逻辑真值表 3、非逻辑函数式 Y=A 4、非逻辑符号 4-1b-y 5、非逻辑运算规则: 0=1 1=0 0'=1 1'=0
三、 非运算 条件具备时,结果不会发生;条件不具备时结果一定 发生。把这种因果关系叫逻辑非,也叫逻辑求反运算。 5 、非逻辑运算规则: 4、 非逻辑符号 2、非逻辑真值表 3 、非逻辑函数式 A Y 0 1 1 0 1 、非逻辑定义 Y = A Y=A´ 0 = 1 1 = 0 0´=1 1´=0
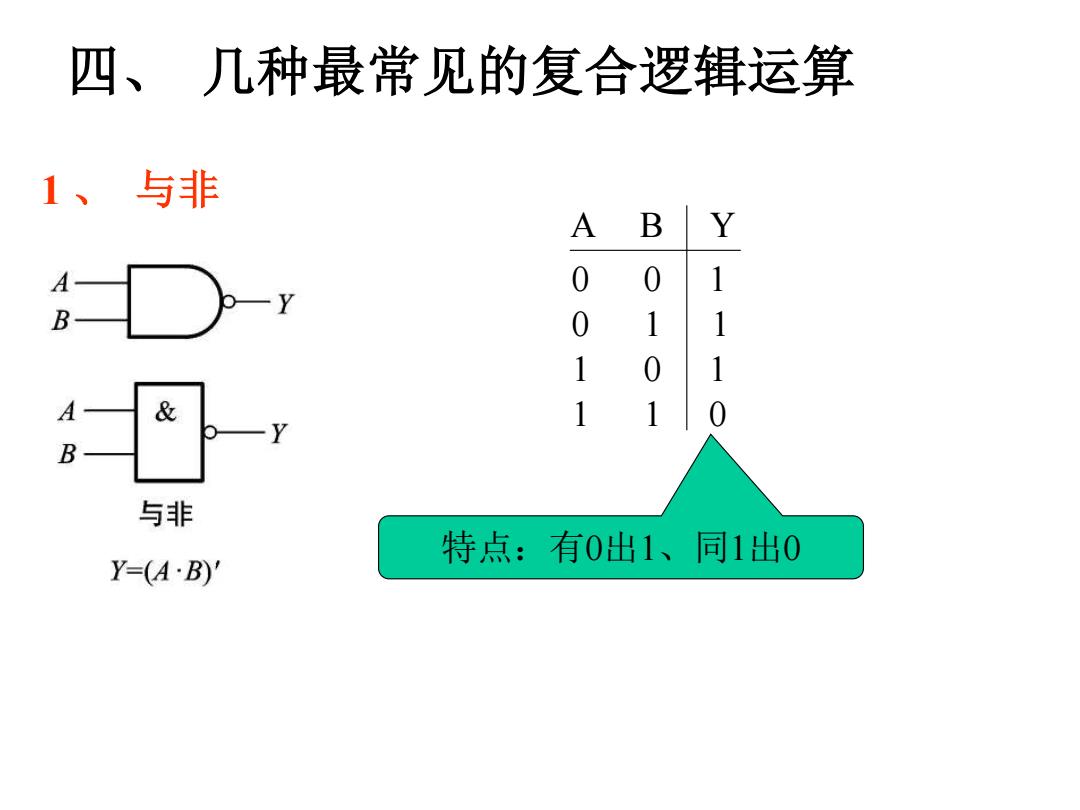
四、几种最常见的复合逻辑运算 1、与非 A B Y A 0 1 B 0 1 与非 特点:有0出1、同1出0 Y=(A·B)
四、 几种最常见的复合逻辑运算 1 、 与非 A B 0 0 0 1 1 0 1 1 Y 1 1 1 0 特点:有0出1、同1出0
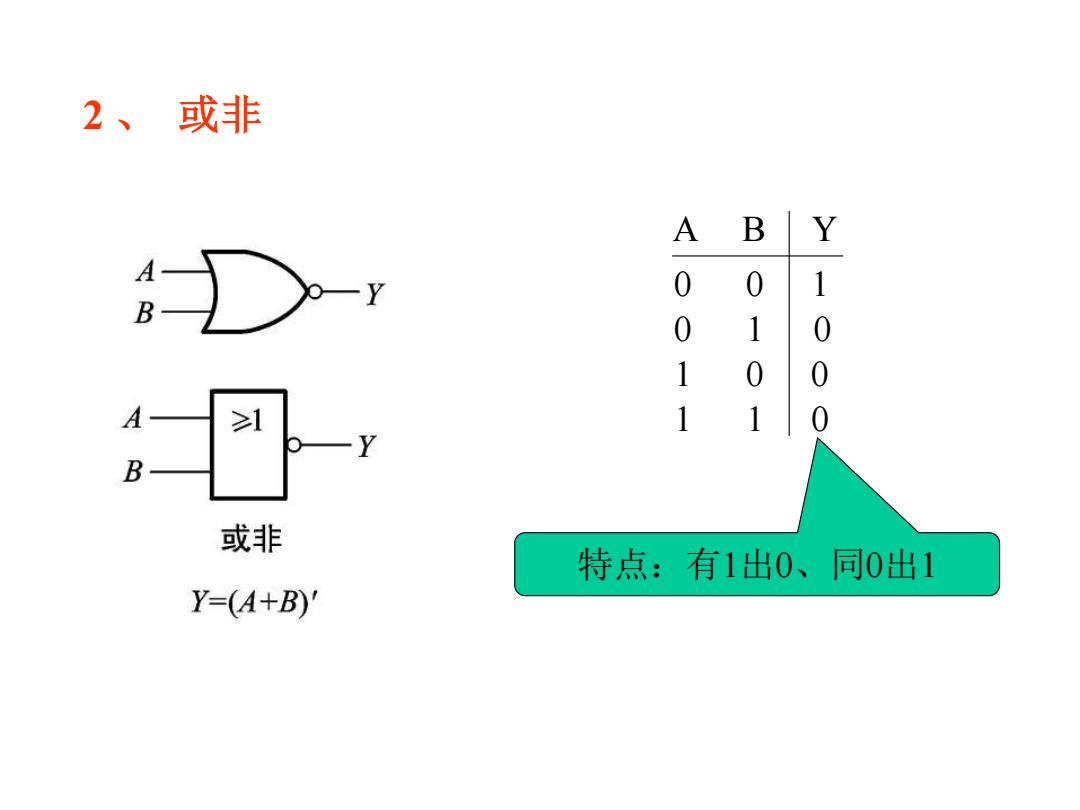
2、或非 A B Y 】 0 0 1 0 1 0 1 0 0 ≥1 1 1 0 或非 特点:有1出0、同0出1 Y=(A+B)
2 、 或非 A B 0 0 0 1 1 0 1 1 Y 1 0 0 0 特点:有1出0、同0出1
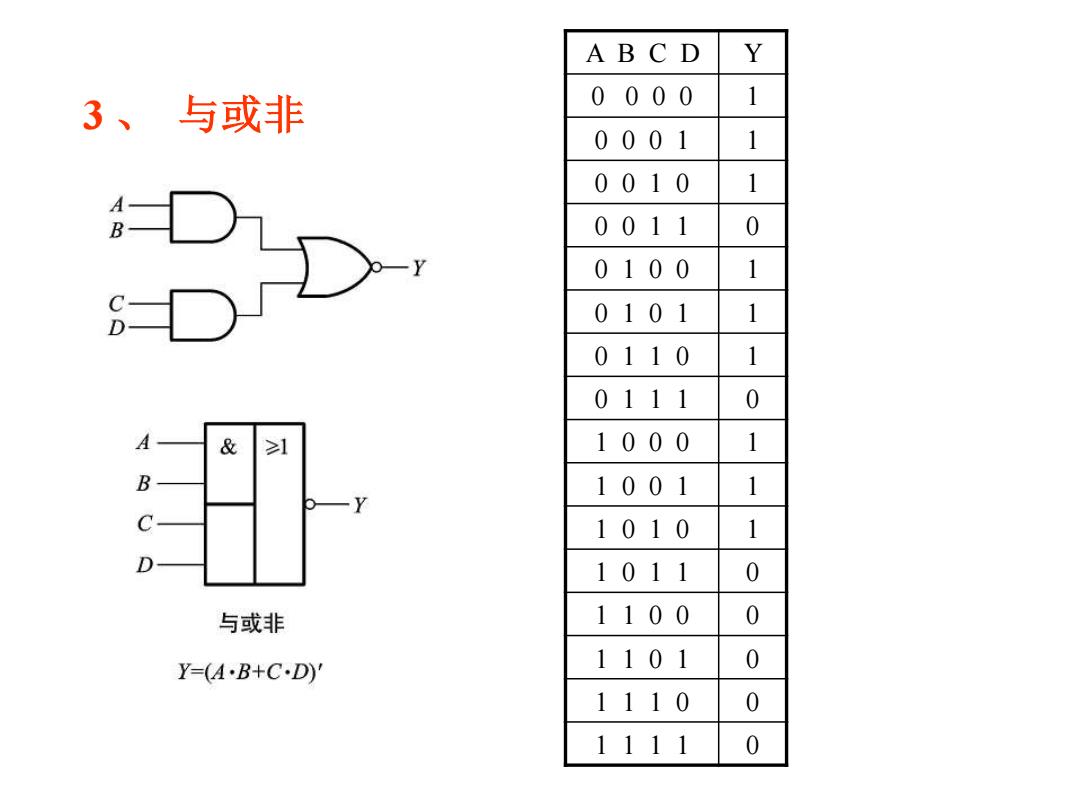
ABCD Y 3、与或非 0000 1 0001 1 0010 1 0011 0 0100 1 0101 1 0110 1 0111 0 A & 1000 1 B 1001 1 C 1010 1 D 1011 0 与或非 1100 0 Y=(AB+C·D)' 1101 0 1110 0 1111 0
3 、 与或非 A B C D Y 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 0 0 1 1 1 1 0
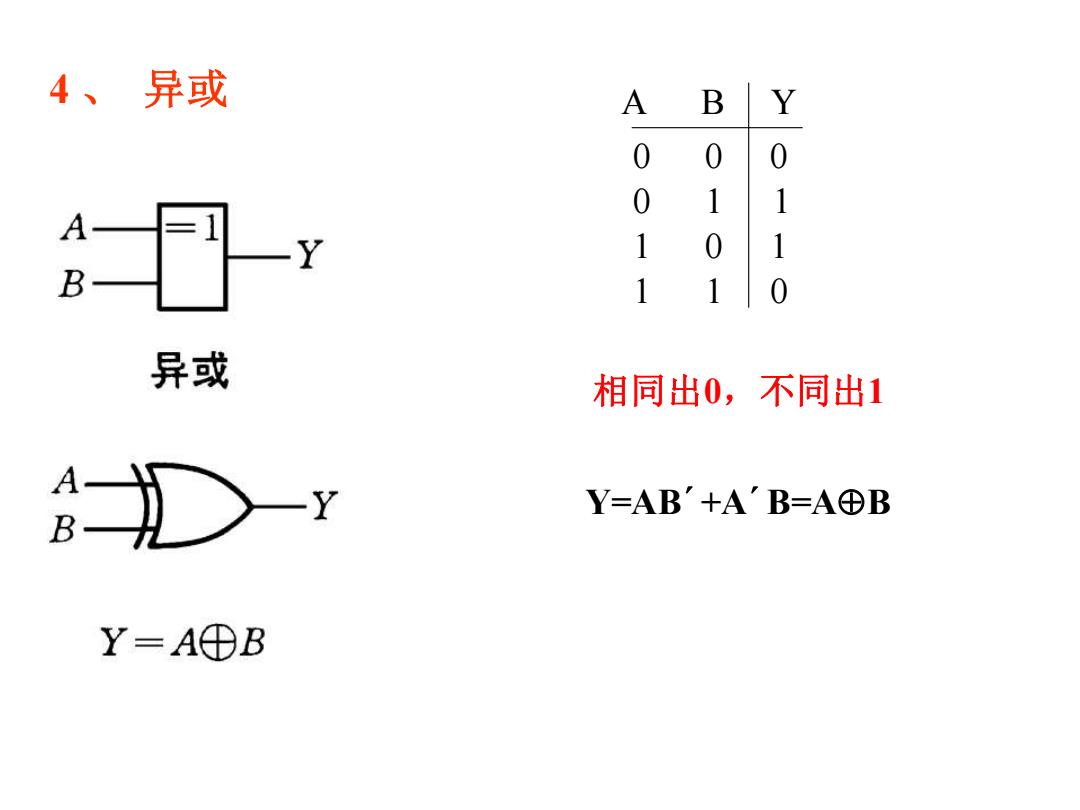
4、异或 A B Y 0 0 0 0 1 1 1 0 1 1 1 0 异或 相同出0,不同出1 Y=AB'+A'B=A⊕B Y=A⊕B
4 、 异或 A B 0 0 0 1 1 0 1 1 Y 0 1 1 0 相同出0,不同出1 Y=AB´+A´B=AB

5、同或(异或非) A B Y 0 0 1 0 1 0 1 0 0 1 11 同或 相同出1、不同出0 8-y Y=A'B'+AB=A⊙B Y=A⊙B
5、 同或(异或非) A B 0 0 0 1 1 0 1 1 Y 1 0 0 1 相同出1、不同出0 Y=A´B´+AB=A⊙B