
23逻辑函数及其描述方法 真值表表示法、逻辑函数式表示法、 逻辑图表示法、波形图表示法、卡诺图表示法等。 例:某一逻辑电路,对输入两路信号A、B进行比较, A、B相异时,输出为1;相同时,输出为0。 试表示其逻辑关系。 输入 输出 一、用真值表描述逻辑函数 Y 函数的真值表就是将输入变 0 0 0 量所有可能的取值与对应的函数 0 1 1 输出值对应列成的表格。 1 0 1 11 0
例:某一逻辑电路,对输入两路信号A、B进行比较, 一、用真值表描述逻辑函数 函数的真值表就是将输入变 量所有可能的取值与对应的函数 输出值对应列成的表格。 A B Y 0 0 0 1 1 0 1 1 0 1 1 0 真值表表示法、逻辑函数式表示法、 逻辑图表示法、 波形图表示法、卡诺图表示法等。 试表示其逻辑关系。 A、B相异时,输出为1;相同时,输出为0。 输 入 输出 2.3 逻辑函数及其描述方法

二、用逻辑函数式描述逻辑函数 把逻辑函数的输出写成输入逻辑变量的代数 运算式,就得到了逻辑函数式。 例:Y=A'B+AB
把逻辑函数的输出写成输入逻辑变量的代数 运算式,就得到了逻辑函数式。 二、用逻辑函数式描述逻辑函数 例:Y=A´B+AB´
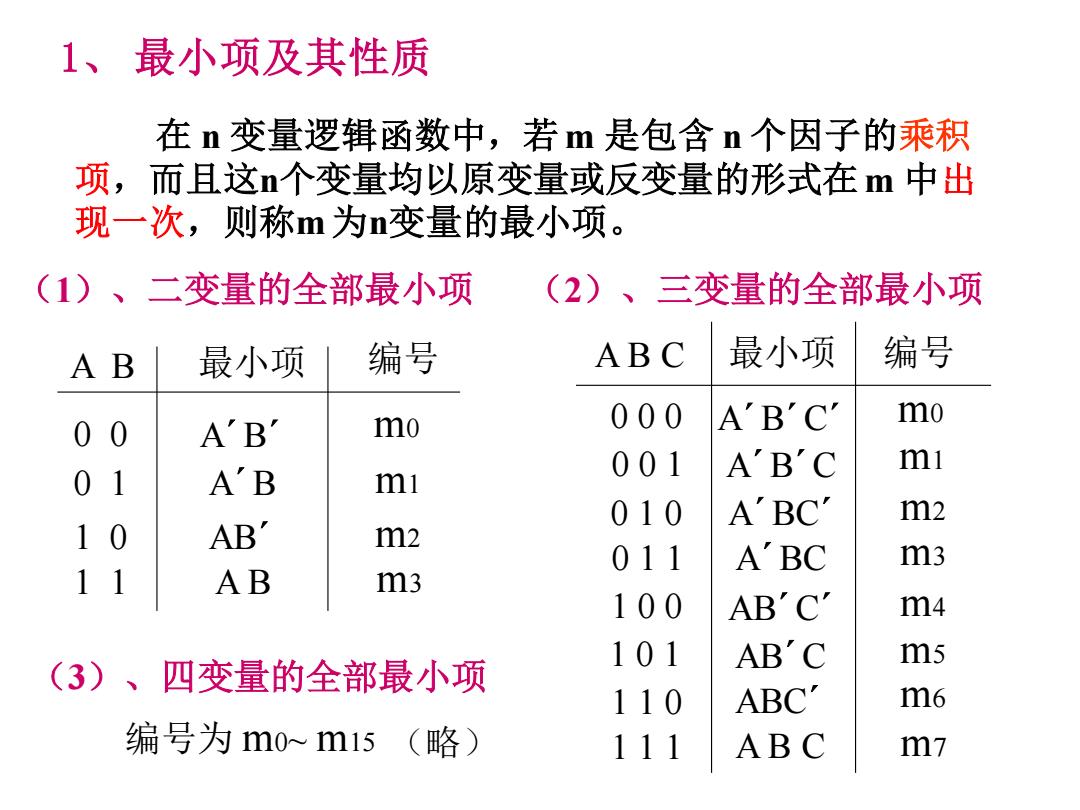
1、最小项及其性质 在n变量逻辑函数中,若m是包含n个因子的乘积 项,而且这个变量均以原变量或反变量的形式在m中出 现一次,则称m为n变量的最小项。 (1)、二变量的全部最小项 (2)、三变量的全部最小项 AB 最小项 编号 ABC 最小项 编号 mo 000 ABC mo 00 AB 01 AB 001 mi AB'C mi 010 ABC m2 10 AB' m2 011 ABC m3 11 AB m3 100 AB'C' m4 (3)、四变量的全部最小项 101 AB'C m5 110 ABC' m6 编号为m0~m15(略) 111 ABC m7
1、 最小项及其性质 (1)、二变量的全部最小项 A B 最小项 编号 0 0 0 1 1 0 1 1 A B A m0 ´B´ A´B AB´ m1 m2 m3 (2)、三变量的全部最小项 A B C 最小项 编号 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 m0 A B C A´B´C´ A´B´C A´BC´ A´BC AB´C´ AB´C ABC´ m1 m2 m3 m4 m5 m6 m7 (3)、四变量的全部最小项 编号为 m0~ m15 在 n 变量逻辑函数中,若m 是包含 n 个因子的乘积 项,而且这n个变量均以原变量或反变量的形式在m 中出 现一次,则称m 为n变量的最小项。 (略)

4变量(A,B,C,D)的最小项: m10: 1010 AB CD' m14: 1110 ABCD
4变量(A,B,C,D)的最小项: m10: 1010 m14: 1110 AB´CD´ ABCD´

n变量的最小项应有2n个 二变量全部最小项有m~m3共4个; 三变量全部最小项有m~m共8个; 四变量全部最小项有m,~m1s共16个; 最小项的性质: 1)在输入变量的任何取值下必有一个且仅有一个最小项的值为1; 2)全体最小项之和为1; 3)任意两个最小项的乘积为0; 4)具有相邻性的两个最小项之和可以合并为一项,合并后的结果 中只保留这两项的公共因子。 (利用公式AB+AB'=A) 只有一个因子不同的两个最小项是具有相邻性的最小项
n变量的最小项应有2 n个 最小项的性质: 2)全体最小项之和为1; 3)任意两个最小项的乘积为0; 1)在输入变量的任何取值下必有一个且仅有一个最小项的值为1; 4)具有相邻性的两个最小项之和可以合并为一项,合并后的结果 中只保留这两项的公共因子。 二变量全部最小项有m0~m3共4个; 三变量全部最小项有m0~m7共8个; 四变量全部最小项有m0~m15共16个; 只有一个因子不同的两个最小项是具有相邻性的最小项。 (利用公式AB+AB´=A)
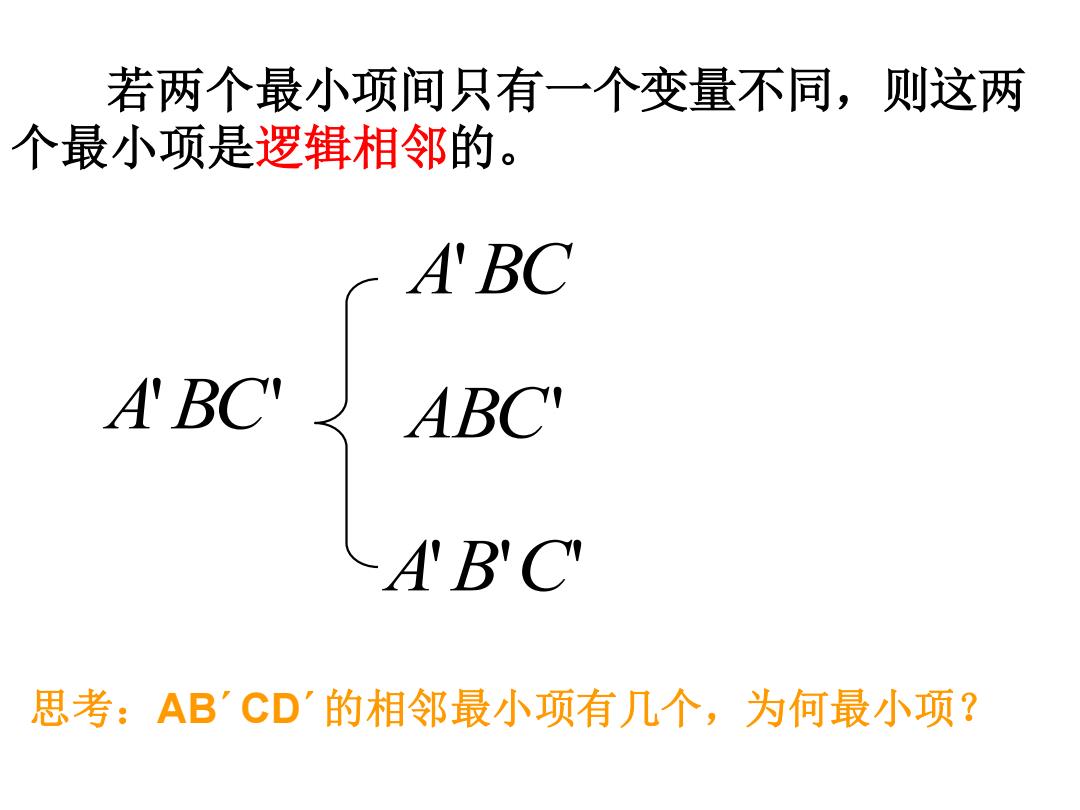
若两个最小项间只有一个变量不同,则这两 个最小项是逻辑相邻的。 ABC ABC 思考:AB'CD'的相邻最小项有几个,为何最小项?
若两个最小项间只有一个变量不同,则这两 个最小项是逻辑相邻的。 A'BC' A'BC ABC' A'B'C' 思考:AB´CD´的相邻最小项有几个,为何最小项?

2、逻辑函数式的最小项之和形式 利用基本公式A+A'=1可以把任何逻辑函数化为最小 项之和的标准形式。 例1:Y(A,B,C)=A'BC+AC'+B'C 解:Y(A,B,C)=A'BC+A(B+B)C'+(A+A')B'C =A'BC+ABC'+AB'C'+AB'C+A'B'C =m3+m6+m4+ms+m1 =2m(1,3,4,5,6)
例1:Y(A,B,C) = A´BC+AC´+B´C 解:Y(A,B,C) = A´BC+A(B+B´)C´+(A+A´)B´C = A´BC+ABC´+AB´C´+AB´C+A´B´C = m3 + m6 + m4 + m5 + m1 = m(1,3,4,5,6) 2、逻辑函数式的最小项之和形式 利用基本公式 A+A´=1 可以把任何逻辑函数化为最小 项之和的标准形式

例2:Y(A,B,C,D)=(AD+A'D'+B'D+C'D')' 解:Y(A,B,C,D)=(AD)'(A'D')'(B'D)'(C'D')' =(A'+D')A+D)(B+D')(C+D) =A'BD+ACD' =A'B(C+C)D+A(B+B)CD =A'BCD+A'BC'D+ABCD'+AB'CD =m7+m5+m14+m10 =2m(5,7,10,14)
例2:Y(A,B,C,D)=(AD+A´D´+B´D+C´D´) ´ 解:Y(A,B,C,D) = (AD) ´(A´D´) ´(B´D) ´(C´D´) ´ = (A´+D´)(A+D)(B+D´)(C+D) = A´BD+ACD´ = A´B(C+C´)D+A(B+B´)CD´ = A´BCD+A´BC´D+ABCD´+AB´CD´ = m7 + m5 + m14 + m10 = m(5,7,10,14)

三、用逻辑图描述逻辑函数 用逻辑图形符号连接起来表示逻辑函数,得到的 连接图称为逻辑图。 (AB') (A'B)' Y(A,B)=((AB)(A'B))' =AB'+AB=A⊕B
三、用逻辑图描述逻辑函数 用逻辑图形符号连接起来表示逻辑函数,得到的 连接图称为逻辑图。 AB A B A B Y A B AB A B = + = = ( , ) (( ) ( ) )
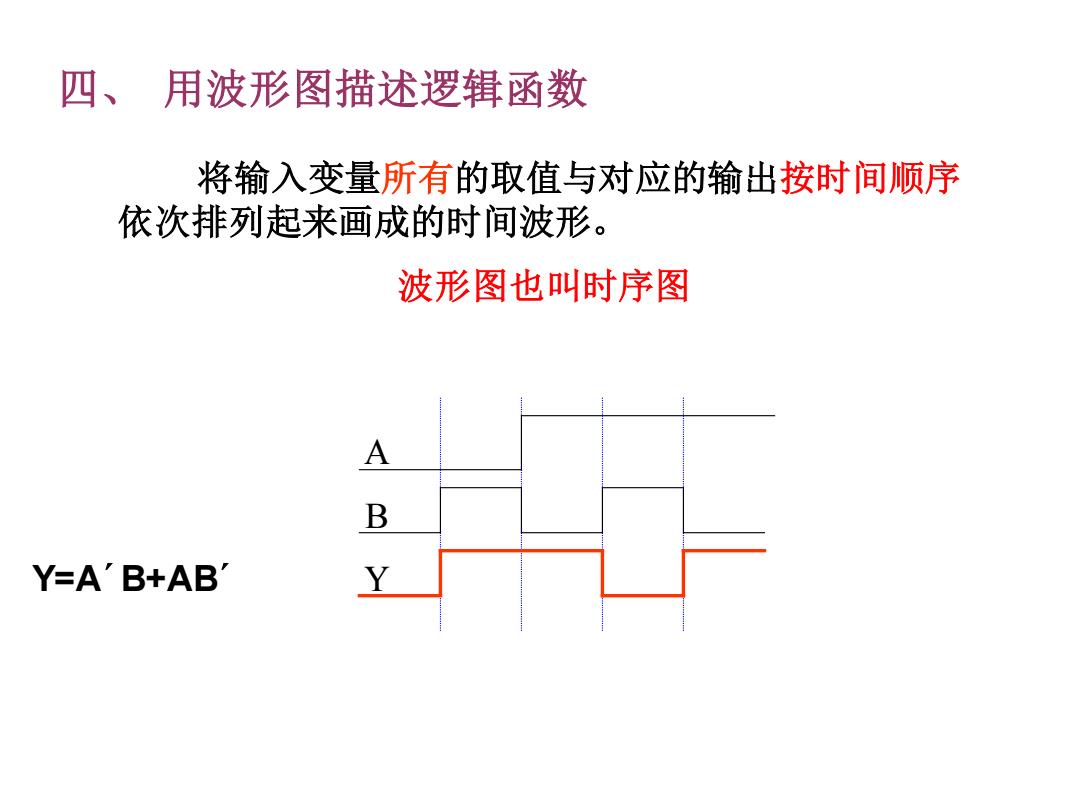
四、用波形图描述逻辑函数 将输入变量所有的取值与对应的输出按时间顺序 依次排列起来画成的时间波形。 波形图也叫时序图 B Y=AB+AB
四、 用波形图描述逻辑函数 A B Y 将输入变量所有的取值与对应的输出按时间顺序 依次排列起来画成的时间波形。 波形图也叫时序图 Y=A´B+AB´