
先进材料疑固实验室 Laboratory of Advanced Materials Solidification 1896 1920 1987 2006 G Heat flow during the solidification process Dr.Mingxu Xia anced Mate 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
1896 1920 1987 2006 Heat flow during the solidification process Dr. Mingxu Xia

先进材料疑固实验室 OUTLINE Laboratory of Advanced Materials Solidification Heat exchange and temperature field Sand mold heat exchange Metal mold heat exchange Solidification mode of castings Concept of casting simulation (Virtual Manufacturing) tory of vanced Materials Solid 上降充通大学 SHANGHAI JIAO TONG UNIVERSITY
OUTLINE Heat exchange and temperature field Sand mold heat exchange Metal mold heat exchange Solidification mode of castings Concept of casting simulation (Virtual Manufacturing)

Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field 3u区.腊 nced Matere 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
Heat exchange and temperature field

Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field Pouring cup Cast metal in cavity Riser Core Cope Downsprue Parting line Runner Flask Drag Mold 777 77777777777, Cope Drag Two sets of castings(bronze and aluminium)from the above sand mold 上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY
Heat exchange and temperature field Cope Drag Two sets of castings (bronze and aluminium) from the above sand mold
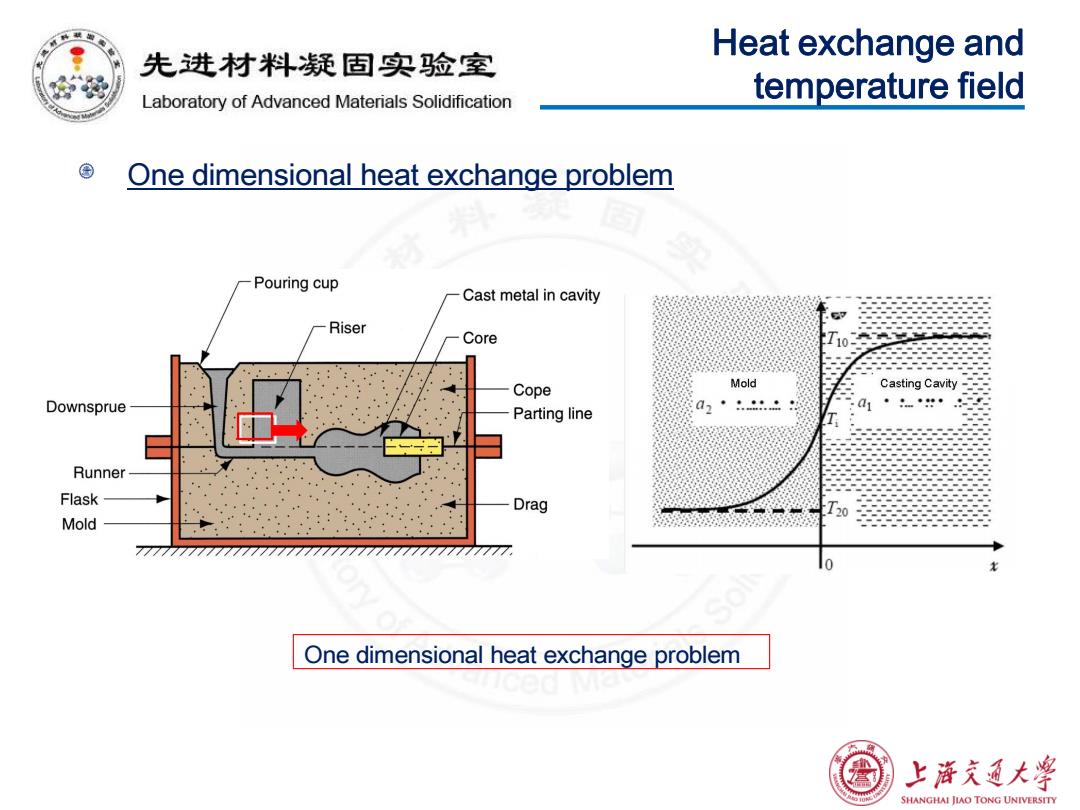
Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field One dimensional heat exchange problem Pouring cup Cast metal in cavity Riser Core Cope Mold Casting Cavity Downsprue Parting line Runner Flask Drag 10 Mold 7777777777777777 One dimensional heat exchange problem 上游充通大学 SHANGHAI JIAO TONG UNIVERSITY
Heat exchange and temperature field One dimensional heat exchange problem One dimensional heat exchange problem

Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field One dimensional heat exchange problem Assumptions: 1.Uniform temperature of mold and mold cavity,Pouring temperature T10,mold temperature T20: 2.Pure metal solidification 3. No latent heat release 4. Parameters:Casting:入1、C1、p1 5. Mold:入2、C2、P2 6. No heat resistance between casting and mold Then: ot 02T &t er2 a---Heat diffusion coefficient,=cp) 上降充通大学 SHANGHAI JIAO TONG UNIVERSITY
Assumptions: 1. Uniform temperature of mold and mold cavity, Pouring temperature T10, mold temperature T20: 2. Pure metal solidification 3. No latent heat release 4. Parameters: Casting: λ1 、c1 、ρ1 5. Mold: λ2 、c2 、ρ2 6. No heat resistance between casting and mold Then: Heat exchange and temperature field One dimensional heat exchange problem α---Heat diffusion coefficient , = λ/(cρ)

Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field One dimensional heat exchange problem The general integral of the equation is T =C+Derf 2√at Where C and D is the constants for indefinite integral,erf(x)is the Gaussian Error Function as erf The value of erf(x)can be obtained from a Chart,as list x=0, erf(x)=0,erf(-x)=-erf(x),erf(co)=1,erf(-co)=-1. 上降充通大学 SHANGHAI JIAO TONG UNIVERSITY
The general integral of the equation is Where C and D is the constants for indefinite integral, erf(x) is the Gaussian Error Function as The value of erf(x) can be obtained from a Chart, as list x=0, erf(x)=0,erf(-x)=-erf(x), erf(∞)=1, erf(-∞)=-1. Heat exchange and temperature field One dimensional heat exchange problem

Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field One dimensional heat exchange problem Initial conditions:For Mold,t=0,Ti=T20; T=C+D=T20(t=0) Boundary conditions:x=0(t>0),T1=T2=Ti T=C=Ti From mold side: T2 =T;+(T;-T20)erf Similarly from casting side: T1=T;+(T1o -T;)erf ced Mat 上降充通大学 SHANGHAI JIAO TONG UNIVERSITY
Initial conditions: For Mold, t=0, Ti=T20; T=C+D=T20(t=0) Boundary conditions: x=0(t>0), T1=T2=Ti T=C=Ti From mold side: Similarly from casting side: Heat exchange and temperature field One dimensional heat exchange problem

Heat exchange and 先进材料疑固实验室 Laboratory of Advanced Materials Solidification temperature field One dimensional heat exchange problem Then easily get: T-%0+a210 a1+Q2 (steady state) a and a corresponding to casting and mold. Substitute this equation to previous one ent va) C1+2 1+2 I+a+aerf(a T= 1+2 a1+a2 nced Materals 上降充通大学 SHANGHAI JIAO TONG UNIVERSITY
Then easily get: α1 and α2 corresponding to casting and mold. Substitute this equation to previous one Heat exchange and temperature field One dimensional heat exchange problem (steady state)

先进材料疑固实验室 Laboratory of Advanced Materials Solidification Sand mold heat exchange For sand casting: Ti(Gin-Ta)er 砂型 困相 液相 Derivate of x is Heat flux went through the interface: 9x=-0=-mx=0 Then 距离x 9x=0= Amcmem (Tm-To) Sand Casting πt vanced Maten 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
For sand casting: Derivate of x is Heat flux went through the interface: Then Sand Casting Sand mold heat exchange