
先进材料疑固实验室 Laboratory of Advanced Materials Solidification 1896 1920 1987 2006 Solidification of multi phase alloys(2) Dr.Mingxu Xia anced Mate 国 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
1896 1920 1987 2006 Solidification of multi phase alloys (2) Dr. Mingxu Xia

先进材料疑固实验室 References Laboratory of Advanced Materials Solidification M.C.Flemings,凝固过程 W.Kuz,凝固原理 介万奇,凝固技术 JA Dantzig,M.Rappaz,Solidification tory of vanced Materials Solid 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
References M.C.Flemings, 凝固过程 W.Kurz,凝固原理 介万奇,凝固技术 JA Dantzig, M. Rappaz, Solidification

先进材料疑固实验室 OUTLINE Laboratory of Advanced Materials Solidification Solidification of Eutectics Coupled eutectic growth morphology Other eutectic morphologies Jackson-Hunt model for Regular eutectics Morphology control method for regular eutectics Model for irregular eutectics Competitive growth of eutectic and dendritic phases Coupled zone in binary alloy phase diagram Solidification of Peritectics Microstructure control through solidification method Solidification Defects 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
OUTLINE Solidification of Eutectics • Coupled eutectic growth morphology • Other eutectic morphologies • Jackson-Hunt model for Regular eutectics • Morphology control method for regular eutectics • Model for irregular eutectics • Competitive growth of eutectic and dendritic phases • Coupled zone in binary alloy phase diagram Solidification of Peritectics Microstructure control through solidification method Solidification Defects
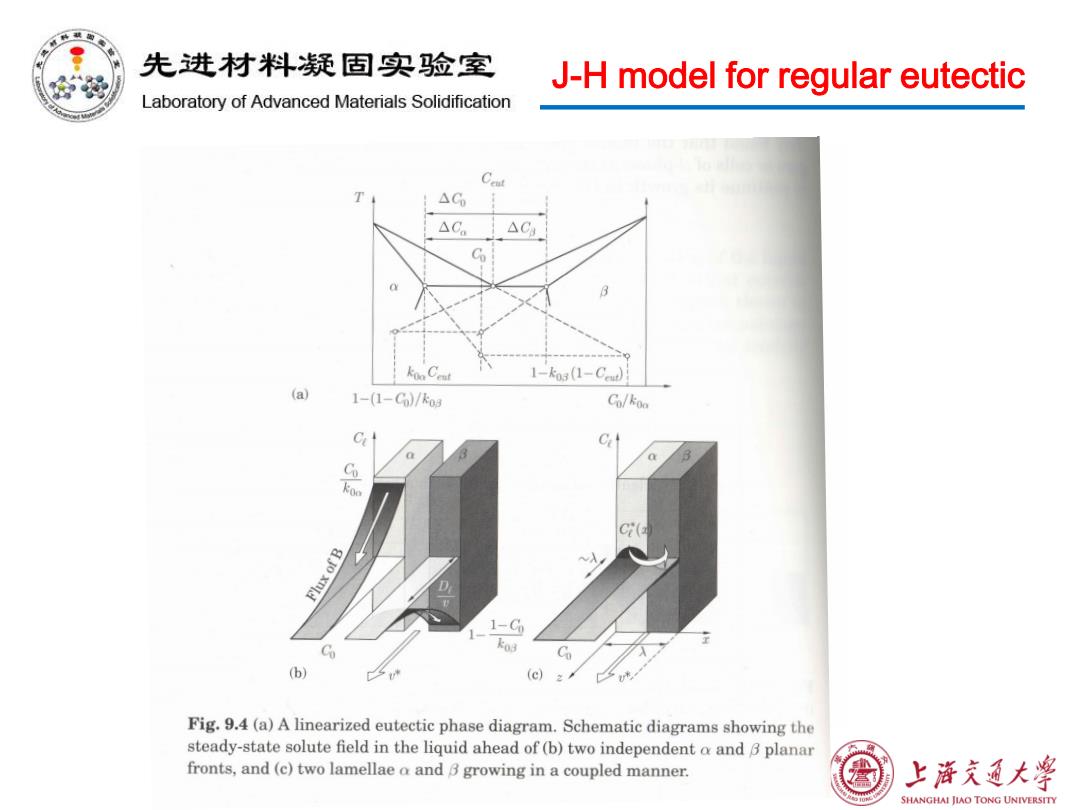
先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification T △G △Ca △C Co 1-k3(1-Ca (a) 1-(1-C0/ko3 Co/koo a a Co Flux of B 1-C ko3 C (b) (c) Fig.9.4(a)A linearized eutectic phase diagram.Schematic diagrams showing the steady-state solute field in the liquid ahead of(b)two independent o and B planar fronts,and (c)two lamellae a and B growing in a coupled manner. 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic
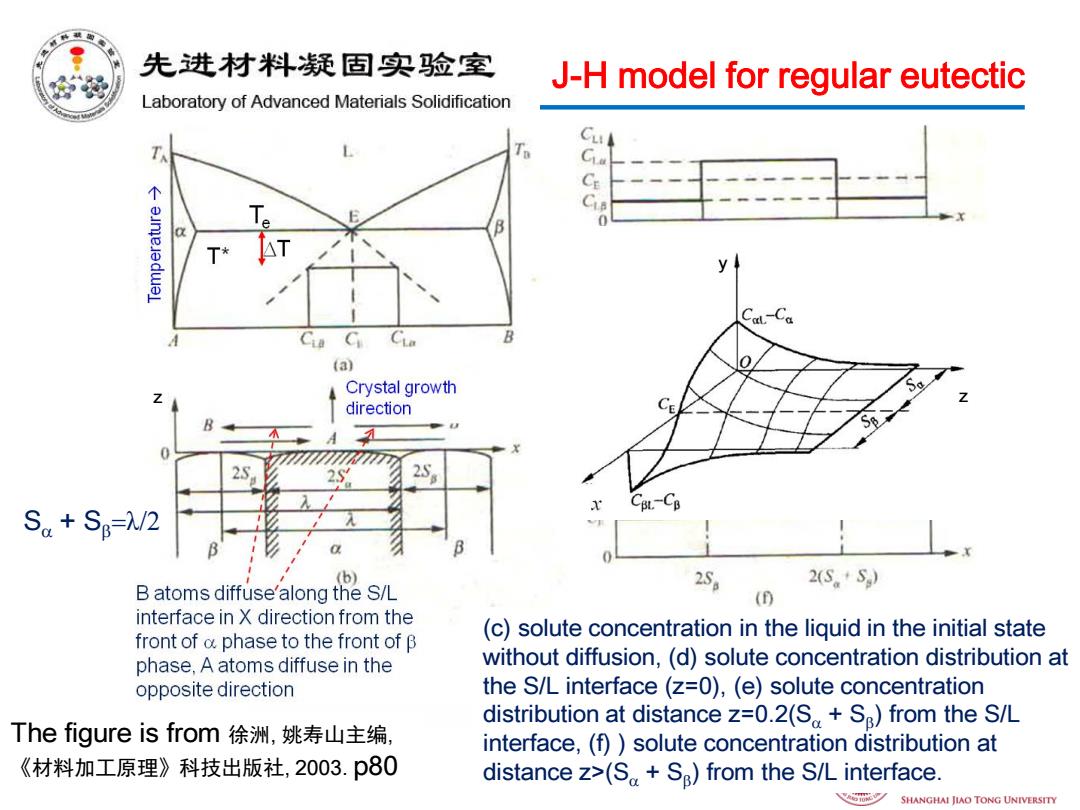
先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification Cu T CE 个 0 AT CLa B (a) Crystal growth direction A 2S BL.-CB Sa+Sg=λ/2 (b) 25。 2S。+S) B atoms diffuse'along the S/L (0 interface in X direction from the front of a phase to the front of B (c)solute concentration in the liquid in the initial state phase,A atoms diffuse in the without diffusion,(d)solute concentration distribution at opposite direction the S/L interface(z=0),(e)solute concentration distribution at distance z=0.2(S+S)from the S/L The figure is from徐洲,姚寿山主编, interface,(f))solute concentration distribution at 《材料加工原理》科技出版社,2003.p80 distance z>(S+Sg)from the S/L interface A SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic (c) solute concentration in the liquid in the initial state without diffusion, (d) solute concentration distribution at the S/L interface (z=0), (e) solute concentration distribution at distance z=0.2(Sα + Sβ) from the S/L interface, (f) ) solute concentration distribution at distance z>(Sα + Sβ) from the S/L interface. The figure is from 徐洲, 姚寿山主编, 《材料加工原理》科技出版社, 2003. p80 y z z Sα + Sβ=λ/2

先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification From the phase diagram,the corresponding solid composition Ca Ce,liquid composition L+a L L+B CaL and CeL have the following relationship: C BM 会k1 Ce =kg>1 A Ca CBL CE CaL B CB/% nced Matere 上浒充通大 SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic From the phase diagram, the corresponding solid composition Cα, Cβ, liquid composition CαL and CβL have the following relationship:

先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification Consider a periodic arrangement of a- C and B-lamellae with a characteristic spacing 1,solidifying at steady state with a constant velocity v*.Symmetry CE permits us to restrict the analysis to the domain xE[0,/2]andz∈[0,ool. CBL.-CB 02C 02C v0Gi 0x20z2 D0z 0 △T Where D,is the diffusion coefficient in Ib) the liquid.The boundary conditions for +%入/2十—/2 the problem are given by ⊕ O 20 Dia x=0,1/2 d Fig.9.9 (a)The solute profile C(r,:ahead of two lamellae a and 3 and (b)the ⊕ CL=Co corresponding solute profile in the liquid at the interface,Ci(r).(c)Assuming an isothermal eutectie front at a temperature T.the difference between the corre ponding liquidus T(C()).=o.3,and T is a direct measure of the curva ture undercooling ATn(r).(d)The Laplace-Young condition at the triple junction a-3-t. ggs is the fraction of a,B phase. 上酒天通大学 SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic Consider a periodic arrangement of α- and β-lamellae with a characteristic spacing λ, solidifying at steady state with a constant velocity ν*. Symmetry permits us to restrict the analysis to the domain x∈[0, λ/2] and z ∈[0,∞]. Where Dl is the diffusion coefficient in the liquid. The boundary conditions for the problem are given by x =0, λ /2 z→∞ gα gβ is the fraction of α, β phase

种 先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification At the eutectic interface z=0,the flux condition should satisfy the following conditions: (az) =-v*Ci(1-koa) z=0,0≤x≤9ax (9)-p1-G1-kag) z=0,9x≤x≤ X gge is the fraction of a,B phase. The x-periodicity of the eutectic structure implies that the solution to 02C02C vOCL D oz 20 Can be obtained by a Fourier series G=C+∑B,cos元e 2πX 2mπ (n≥1) 1=1 熟 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic At the eutectic interface z=0, the flux condition should satisfy the following conditions: The x-periodicity of the eutectic structure implies that the solution to Can be obtained by a Fourier series gα gβ is the fraction of α, β phase. (n≥1)

先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification Where Bn= 1v*△C0 (nI)2D sin(nnga) n≥1,AC=(4Ca+△Cg) =direction,there is no diffusion in solid,x direction,Ca and Ce can be expressed as ca=k(Co+∑ 2nnx B.cos a 0≤x≤Sa n=1 cp-k+∑.os2 0 2nnx Sasx≤Sa+SB n=1 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic Where z direction, there is no diffusion in solid, x direction, Cα and Cβ can be expressed as

先进材料疑固实验室 J-H model for regular eutectic Laboratory of Advanced Materials Solidification According to the solute distribution in front of the eutectic interface and the geometry feature at the interface,the undercooling at the interface is the combination of solutal undercooling and curvature undercooling,which is "A T=Ac AR Jackson-Hunt Model D where 00 ACo Imiallmigl sin2(nnga) Ja9g mial+-mue,台 (nI)3 ma 2Tacos02Tcos0 AR-ml+mmialga miglog 上浒充通大学 SHANGHAI JIAO TONG UNIVERSITY
J-H model for regular eutectic According to the solute distribution in front of the eutectic interface and the geometry feature at the interface, the undercooling at the interface is the combination of solutal undercooling and curvature undercooling, which is where Jackson-Hunt Model