
第三章导数的应用 第五节函数的极值与最大值最小值 一、函数的极值及其球法 1.极值的定义 定义设函数f(x)在点和的某一邻城(和)内有定义,若对于 xeU(),均有 f(x)f(xo)) 则称寸(x)是函数f(x)的一个极大值〔或极小值) 函数的极大值与极小值统称为函数的极值:使函数取得极值的点称为极值点, 注1'极值概仑是一个局部性报念, 极大值未必大于极小值。 如图:极大值f(x2),f(x4),f(x) 极小值f(x),f(x),f红3)f(x)0名”面 极大值f(x)<极小值f(x) 之极值与最值的联系与区别:极值是局部性抵念,而最值是整体性概念极 值未必是最值,最值也未必是极值函数在开区间内的最值必是极值
1 第 三 章 导数的应用 第五节 函数的极值与最大值最小值

2.函数取得极值的必要条件 定理1)若数在点处取得极值,且该点具有导数,则必有()=0 2)若函数在点处x取得极值,则必有'(石)=0或'(和)不存 在 【简言之,函数的极值点必为驻点与不可导点,可导函数的极值点必为 驻点】 证)设(x)在×,处取得极大值,即(,),使 f(x)<f(x),x∈0(x,),则当ב×,时 1,0w-生0 x-X0 当×〉×,时 -<0,从而 x-0 a-典0 故∫'(x0)=0 2)如f(x)=在点x=0处取得极小值,而在该点处f(x)不可导 ■ 注驻点与不可导点不一定都是极值点,即 (f(x)的极值点}C《f(x)的驻点}U(f(x)的不可导.点}
2
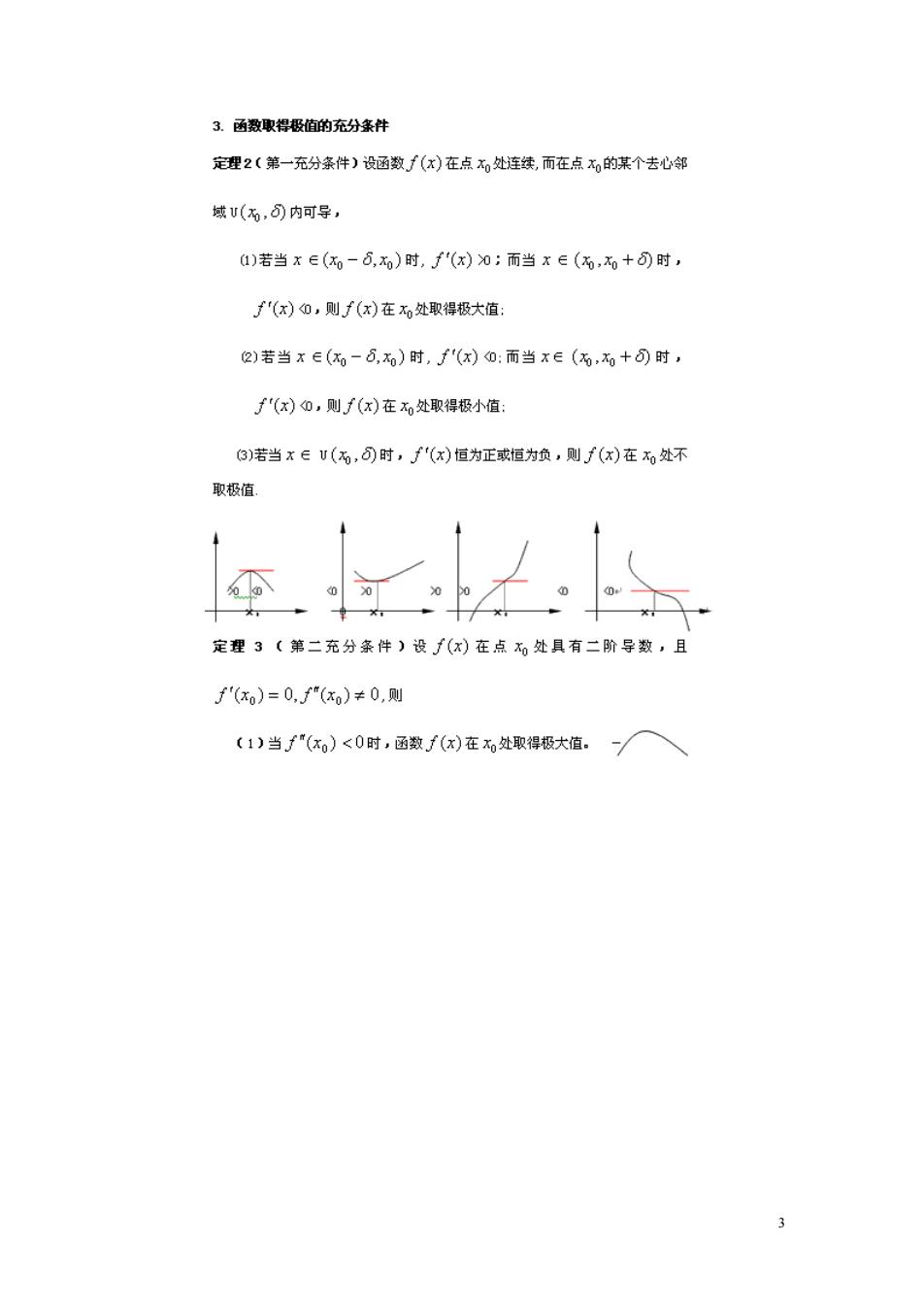
3.函数取得极的充分条件 定理2(第一充分条件)设函数(x)在点和处连续,而在点的某个去心部 城(,)内可导, )若当x∈(伍-6,x)时,f"(x)刀:而当x∈(,0+)时, f"(x)①,则f(x)在和处取得极大值: 2)若当x∈(0-6,0)时,f"(x)0:而当x∈(而,和+时, (x)0,则f(x)在处取得极小值 3)若当x∈v(,可时,∫"(x)恒为正或恒为负,则f(x)在x处不 取极值 定理3〔第二充分条件)设∫(x)在点和处具有二阶导数,且 f(x)=0.f(x)≠0,则 (1)当f"(xo)<0时,函数f(x)在x处取得极大值.。一
3

(2)当f"(红,)>0时,函数f()在处取得极小值。人 正1烟了化)-只园0:当x>和时,f"(x)<0.因此,f(x)在 ×,处取得极大值 〔2)同理可证.■ 4求函数设值的一报解影步柔 1)写出函数f(x)的定义城: (1)写出函数f(x)的定义城: 2)求f代x) 2)求f(x.f(x) 3)求f(x)的班点与不可导点 3)求f(x)的驻点: (4)列表讨论 ④)计算驻点处的二阶导数值,并确 定其符号,此写出结 论 5)写出结论
4

例1求通数y=2x3-5x产的极值 解ú)函数y的定义域为(-00,十0o)。 y. 31 3)令y=0,得x=1:当x=0时,y不存在 -.000,01 (1.+0 0 0\0 0 由上表可知,y(0)=0为极大值:y()=-3为极小值 例2求通数y=2x2-3x2的极值 解ú)函数的定义城为(-00,+oo) 2)y=6x2-6x=6x(x-1) y=12x-6 3)令y=0得,x=0,x=1 )y(0=-60,y0)=0是极大 值:y(①=-1是极小值. 5
5

例3求涵数f(x)=(x2-1)3+1的极值。 解(1)函数的定义域为(-60,十0) 2)f"()=3x2-1)2.2x=6x(x+1)2(x-1)2 /(x)=6(x2-1)2+12x(x2-102x=6(x2-05x2-10】 (3)由f'(x)=0得x1=-1x2=0,x3=1 〔4)列表讨论 x (-co,-10 (-1,0) 0 f"(x) 0 f(x) 0 0 0 5)由上表可知,f(0)=-1是极小值,而在x=-1,x=1处不取极 值 一、是大值、最小值问要 1.闭区间上的连续函数的最值 若函数f(x)在[a,b]上连续,则球(x)在[a,b]上的最值的-搬方法 与步骤如下: (1)求导数(x): 6
6

(2)求f(x)在(a,b)内的所有可能级值点.设为,五,大 (3)计笪f(x),f(x),.,f(x)及f(@),()并加以比较其中最 大者即为最大值,最小者即为最小值 1宝f6)=-4x在6,8上的虽值 是闭=881 3 Γ33 含f"(x)=0得x=-1,x=1:当x=0时,f()不存在 由于f仕1)=-3.f0=0.f(±8=240. 故(x)在8,8上的最小值为f(仕1)=-3:最太值为f仕8)=240 例2求函数f(x)=3x-8x2在【-1,1]上的最大值与最小值 解()=12x3-24x2=12x2(x-2) 由f"(x)=0得驻点x=0,x=2E(←1)(舍去). 因f0)=0,f-1)-11,f0)=-5, 故f(x)在【-1,11上的最大值为f(1)=11,最小值为f(①=-5 2.在某区间内只有一个极值点的链续函数的最值 设∫(x)在某区间工内连线且只有一个极值点
7

若f(x)是极太值则J(x)即为f(x)在工内的量大值 )若寸()是极小值则J()即为f(x)在工内的最小德 侧3求f(x)=x+4x的最值 量了(x)的定义域为(-0+o) f"()=4x2+4=4(x2+1) 全f(x)=0,得x=-1驻 点惟一) 因为f(-1)=12>0,故f(-1)=-3悬f(x)的级小值丛面地是 寸(x)的最小值。寸()设有最大值 3.实际问的最值 在某些实际问题中,如果由问题的性质就可断定目标涵数/(x)确有最太 值或量小值面且一定在寸(x)的定义区间内部取得,而J(x)在定义区间内部 只有一个注点,则咳驻点即为所球之最值点 例4心.1B113)从一块半径为R的圆铁片上挖去一个扇形做成一漏斗,问留 下的扇形的中心角取多大时,做成的漏斗容积最大 解设漏斗的半径为x,高为则 2=R,批得r=R,且=VR-=R-R 2元
8

品-可 (0<p<2m 令f网=4r0-d则f(例=16rg-6=2d8r2 3w2) hR -0-g-2Se029 显然(网的最大值点即为V的最大值点由题意,V的最大值一定存在,龄 当P=25时漏科每联y大 作业:卫.180x.3-513,6,9)342)68
9