
《高等数学》 第一章极限与连续
《高等数学》 第一章极限与连续

第一节 初等函数 高等数学 函数的有关概念 反函数 基本初等函数 复合函数、初等函数 建立函数关系举例 米列
一 函数的有关概念 反函数 基本初等函数 二 复合函数、初等函数 三 四 第一节 初等函数 高等数学 五 建立函数关系举例

、函数的有关概念 1.函数的定义 定义设D是一个给定的非空实数集,如果对于 每一个数x∈D,按照一定的对应关系,都有唯一 确定的y值与之对应,则称y是x的函数,记作 :f(x) 数集D叫做这个函数的定义域 因变量 自变量 eD时,称f()为函数在点x,处的函数值 函数值全体组成的数集 y=f(x),x∈D称为函数的值域
因变量 自变量 , ( ) . 当x0 D时 称f x0 为函数在点x0处的函数值 { ( ), } 称为函数的值域. 函数值全体组成的数集 W = y y = f x x D 按照一定的对应关系,都有唯一 确定的 y 值与之对应,则称 y是x的函数,记作 定义 设D是一个给定的非空实数集,如果对于 y = f ( x) 数集D叫做这个函数的定义域 每一个数x D, 1.函数的定义 一、函数的有关概念

函数的两要素:定义域与对应法则 对应法则 自变量 f(xo) 因变量 约定:定义域是自变量所能取的使算式有意义 的一切实数值. 例如,y=1-x2 D:[-1,1川 例如,y= D:(-1,1) 1-x2
( ( ) ) 0 x ( ) 0 f x 自变量 因变量 对应法则f 函数的两要素: 定义域与对应法则. x y D W 约定: 定义域是自变量所能取的使算式有意义 的一切实数值. 2 例如, y = 1− x D :[−1,1] 2 1 1 x y − 例如, = D :(−1,1)

么2.函数的定义域 在实际问题中,应根据问题的实际意义来确定定义域.对 于用数学式子表示的函数,它的定义域可由函数表达式 本身来确定,即要使运算有意义,一般应考虑以下几点: (1)分式中,分母不能为雯 (2)在根式中,负数不能开偶次方根, ● (3)在对数式中,真数不能为零和负数: (4)在三角函数式中,kx+兀(k∈Z不能取正 2 切,kπ(k∈Z)不能取余切; 在反三角函数式中,要符合反三角函数的定 义域; 函数表达式中含有分式,根式、对数式或反三 则应取各部分定义域的交集
2.函数的定义域 • 在实际问题中,应根据问题的实际意义来确定定义域. 对 于用数学式子表示的函数,它的定义域可由函数表达式 本身来确定,即要使运算有意义,一般应考虑以下几点: • (1)分式中,分母不能为零; • (2)在根式中,负数不能开偶次方根; • (3)在对数式中,真数不能为零和负数; • (4)在三角函数式中, 不能取正 切, 不能取余切; • (5)在反三角函数式中,要符合反三角函数的定 义域; • (6)如函数表达式中含有分式、根式、对数式或反三 角函数式,则应取各部分定义域的交集 ( ) 2 k + k Z k (k Z)
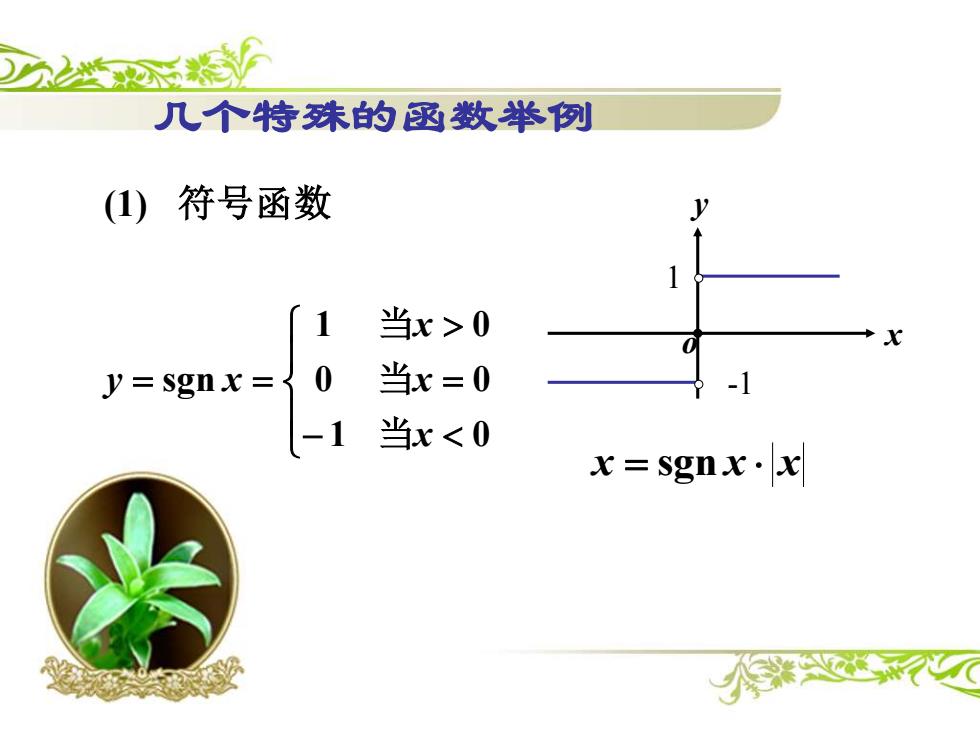
几个恃殊的函数举例 (1)符号函数 1 当x>0 y=sgnx= 当x=0 -1 当x<0 x=Sgnx·x
(1) 符号函数 − = = = 1 0 0 0 1 0 sgn x x x y x 当 当 当 几个特殊的函数举例 1 -1 x y o x = sgn x x

(2)取整函数y=x x表示不超过x的最大整数 d ●0 4-3-2-1.0112345x 23 .4 阶梯曲线
(2) 取整函数 y=[x] [x]表示不超过x 的最大整数 1 2 3 4 5 -2 -4 -4 -3 -2 -1 4 3 2 1 -1 -3 x y o 阶梯曲线
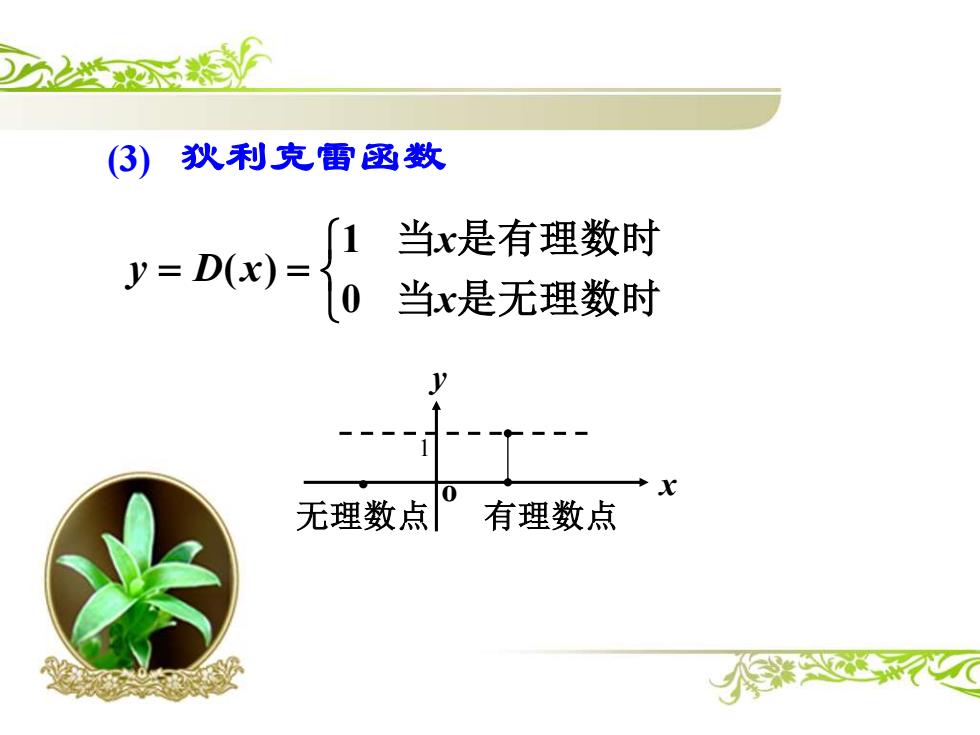
3) 狄利克雷函数 [1当x是有理数时 y=D(x)= 0 当x是无理数时 y 无理数点有理数点 米兴《
= = 当 是无理数时 当 是有理数时 x x y D x 0 1 ( ) 无理数点 有理数点 • 1 x y o (3) 狄利克雷函数
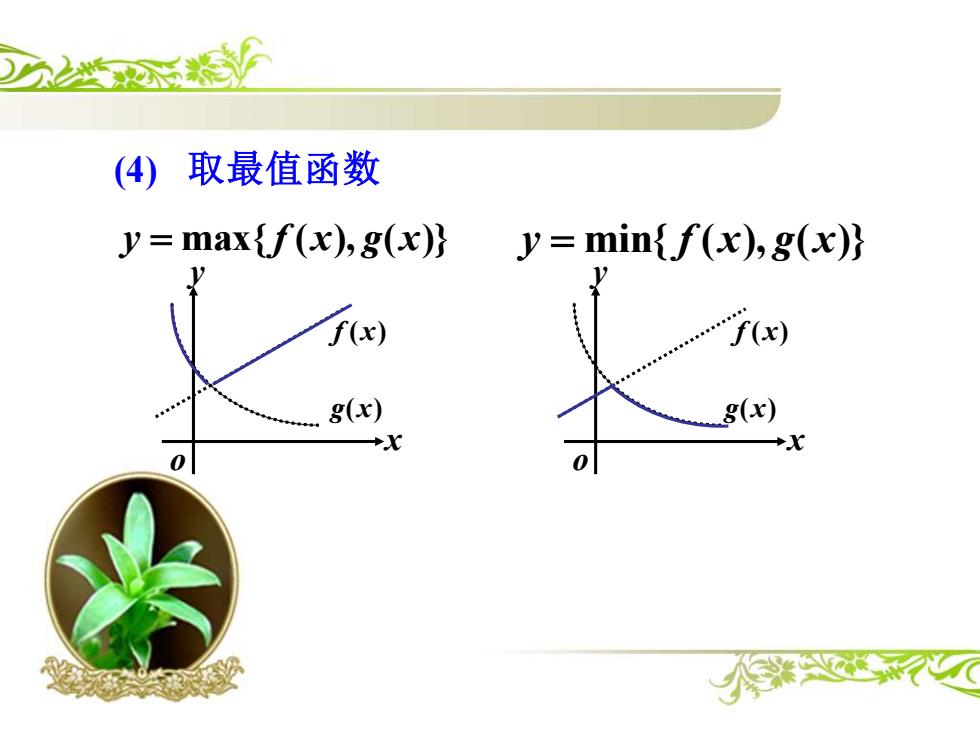
(4)取最值函数 y=maxif(x),g(x)} y=min{f(x),g(x) f(x) "f(x) g(x) 8(x) +0 0
(4) 取最值函数 y = max{f (x), g(x)} y = min{ f (x), g(x)} y x o f (x) g(x) y x o f (x) g(x)

在自变量的不同变化范围中,对应法则用不同的 式子来表示的函数,称为分段函数 2x-1,x>0 例如,f(x)= x2-1,x≤0 y=x2-1 y=2x-1
− − = 1, 0 2 1, 0 , ( ) 2 x x x x 例如 f x 1 y = 2x − 1 2 y = x − 在自变量的不同变化范围中,对应法则用不同的 式子来表示的函数,称为分段函数