
第七节 函数的连续性 一、 函数的连续性 二、函数的间断点 三、初等函数的连续性 四、闭区间上连续函数的性质 五、小结 ☑合
第七节 函数的连续性 一、函数的连续性 二、函数的间断点 三、初等函数的连续性 四、闭区间上连续函数的性质 五、小结

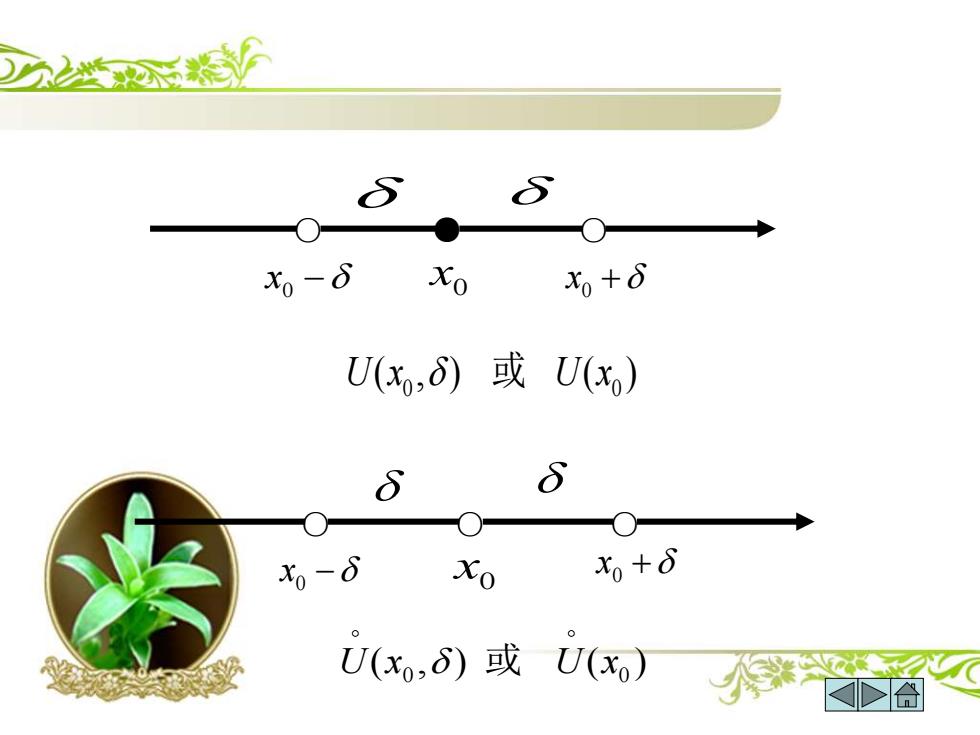
邻域与空心邻域(补从内容) 设x。∈R,6>0,称开区间(x。-6,x。+6)为点x的邻域, 记为U(x,δ), 即U(x,6)=(x。-6,x。+6)={x‖x-xKδ}, x为邻域的中心,δ为邻域的半径 将的s邻域中心x去掉后得x,的6空心邻域,记为U°(x,δ) =(x-δ,x)U(xo,x+δ)={x|0x-xkδ} 或及空心邻域分别简记为U(x)与U°(x)
邻域与空心邻域(补从内容) ( , ), , 0, ( , ) 0 0 0 0 0 U x x R x x x 记为 设 称开区间 − + 为点 的 邻域, 0 0 0 0 即U x x x x x x ( , ) ) { || | }, = − + = − ( , x0 为邻域的中心,为邻域的半径 o 0 0 0 0 将x x x U x 的 邻域中心 去掉后得 的 空心邻域,记为 ( , ), o 0 0 0 0 0 0 即U x x x x x x x x ( , ) { | 0 | | } = − + = − ( , )( , ) 0 0 0 ( ) ( ) o 点x U x U x 的邻域及空心邻域分别简记为 与
S S x,-6 Xo x0+6 U(x,6)或U(x) δ 8 七,-6 Xo x0+6 U(x,)或U(x) ✉囧
○ ● ○ x0 − x0 + 0 x x0 − x0 + 0 x ○ ○ ○ ( , ) ( ) 0 0 U x U x 或 ( , ) ( ) 0 0 U x 或 U x

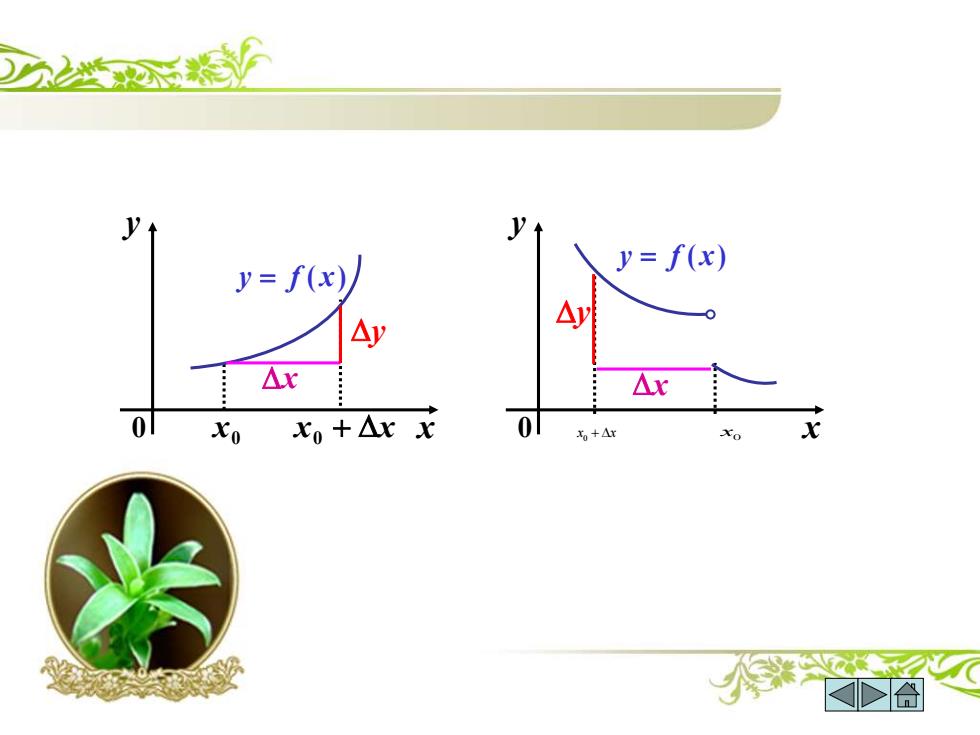
函数的连续性 1.函数的增量 设函数f(x)在U(x)内有定义,廿x∈U(x), △x=x-x,称为自变量在点x,的增量 x:x0→x0+△x △y=f(x)-f(x),称为函数f(x)相应于△x的增量 f(x):f(x)→f(x+△) 作米吃 ✉合
一、函数的连续性 1. 函数的增量 0 0 0 0 ( ) ( ) , ( ), , . f x U x x U x x x x x = − 设函数 在 内有定义 称为自变量在点 的增量 ( ) ( ), ( ) . y = f x − f x0 称为函数 f x 相应于x的增量 x x → x + x 0 0 : ( ): ( ) ( ) 0 0 f x f x → f x + x
y=f(x) y=f(x) y Ay △x △x 0 Xo xo+△xx 0 Xo
x y 0 x0 x0 + x y = f ( x) x y x y 0 x + x 0 x0 x y y = f ( x)

2.连续的定义 定义1设函数f(x)在U()内有定义,如果当自变量的增 量△x趋向于零时,对应的函数的增量△y也趋向于零,即 AiAy=0 或imLf(x+△)-f(x川=0, 那末就称函数f(x)在点x,连续,x,称为f(x)的连续 点. 设x=x,+△,Ay=f()-f(x,人 △x→0就是x→x, △y→0就是fx)→f求 米泛
2.连续的定义 定义1 设函数 f (x)在 0 U x( ) 内有定义,如果当自变量的增 量x 趋向于零时,对应的函数的增量y也趋向于零,即 lim 0 0 = → y x 或 lim[ ( 0 ) ( 0 )] 0 0 + − = → f x x f x x , 那末就称函数 f (x)在点x0 连续, x0 称为 f (x)的连续 点. , 设 x = x0 + x ( ) ( ), 0 y = f x − f x 0 , x → 就是 x → x0 0 ( ) ( ). x0 y → 就是 f x → f

定义2设函数f(x)在U,(x)内有定义,如果 函数f(x)当x→x,时的极限存在,且等于它在 点x,处的函数值f(x),即 lim f(x)=f(x) x->Xo 那末就称函数f(x)在点x连续, 这个定义指出了函数y=f(x)在点x,处满足以下三个条件 (1)函数f(x)在点x及其近旁有定义: 2)limf(x)存在; x→x0 倒数)在r→时的极限值等于⑨
定 义 2 设函数 f (x)在 ( ) U x0 内有定义,如 果 函 数 f (x)当 x → x0 时的极限存在,且等于它在 点x0 处的函数值 ( ) x0 f ,即 lim ( ) ( ) 0 0 f x f x x x = → 那末就称函数 f (x)在点 x0连续. 这个定义指出了函数y = f (x)在点x0 处满足以下三个条件 0 (1) ( ) 函数f x x 在点 及其近旁有定义; 0 2 lim ( ) x x f x → ( ) 存在; 0 0 (3 ( ) )函数f x x x x x 在 → = 时的极限值等于在点 的函数值

例1试证函数f(x)= xsin,x≠0,在x=0 0,x=0, 处连续, 证.f(0)=0, lim xsin=0, x→0 X 即 lim f(x)=f(0), x)0 由定义2知,函数f(x)在x=0处连续 米形 合
例1 . 0 0, 0, , 0, 1 sin ( ) 处连续 试证函数 在 = = = x x x x x f x 证 0, 1 lim sin 0 = → x x x f (0) = 0, 由定义2知, 函数 f (x)在x = 0处连续. lim ( ) (0), 0 f x f x = → 即

3.单侧连续 若函数f(x)在(a,x内有定义,且f(,-0)=f(x), 则称f(x)在点x处左连续; 若函数f(x)在xp,b)内有定义,且f(x+0)=f(x), 则称f(x)在点x处右连续 定理 函数f(x)在x,处连续台是函数f(x)在x, 处既左连续又右连续
3.单侧连续 ( ) ; ( ) ( , ] , ( 0) ( ), 0 0 0 0 则称 在点 处左连续 若函数 在 内有定义 且 f x x f x a x f x − = f x 定理 . ( ) ( ) 0 0 处既左连续又右连续 函 数 f x 在 x 处连续 是函数 f x 在 x ( ) . ( ) [ , ) , ( 0) ( ), 0 0 0 0 则称 在点 处右连续 若函数 在 内有定义 且 f x x f x x b f x + = f x

例2讨论函数fx)= x+2,x20, 在x=0处的 x-2,x<0, 连续性. lim f(x)=lim(x+2)=2-f(0), lim f(x)=lim(x-2)=-2 f(0), x-0- x-0 右连续但不左连续, 故函数f(x)在点x=0处不连续
例2 . 0 2, 0, 2, 0, ( ) 连续性 讨论函数 在 = 处 的 − + = x x x x x f x 解 lim ( ) lim( 2) 0 0 = + → + → + f x x x x = 2= f (0), lim ( ) lim( 2) 0 0 = − → − → − f x x x x = −2 f (0), 右连续但不左连续 , 故函数 f (x)在点x = 0处不连续