第六章定积分及其应用 6.1定积分的概念及性质 6.2定积分的计算方法 6.3非正常积分 6.4定积分的应用
第六章 定积分及其应用 6.1 定积分的概念及性质 6.2 定积分的计算方法 6.3 非正常积分 6.4 定积分的应用

6.4定积分的应用 微元法 。定积分在几何学、物理学、经济学等方面有着广泛 而有效的应用,显示了它的巨大魅力. ·定积分的所有应用问题,一般可按“分割,近似,求和, 取极限”把所求总量表示为定积分.简化为“微元法”. 设y=f(x)是区间[a,b]上的连续函数,为求与f(x) 有关的某一总量Q,先取[α,b]内的任意小的代表 区间x,x+dx],总量Q的微小增量△Q的近似值为 △Q≈f(x)dx
6.4 定积分的应用 ⚫ 定积分在几何学、物理学、经济学等方面有着广泛 而有效的应用,显示了它的巨大魅力. ( ) [ , ] ( ) Q [ , ] [ , ] Q Q y f x a b f x a b x x dx = + 设 是区间 上的连续函数,为求与 有关的某一总量 ,先取 内的任意小的代表 区间 ,总量 的微小增量 的近似值为 一. 微元法 ⚫ 定积分的所有应用问题,一般可按“分割,近似,求和, 取极限”把所求总量表示为定积分. 简化为“微元法”. Q ( ) f x dx
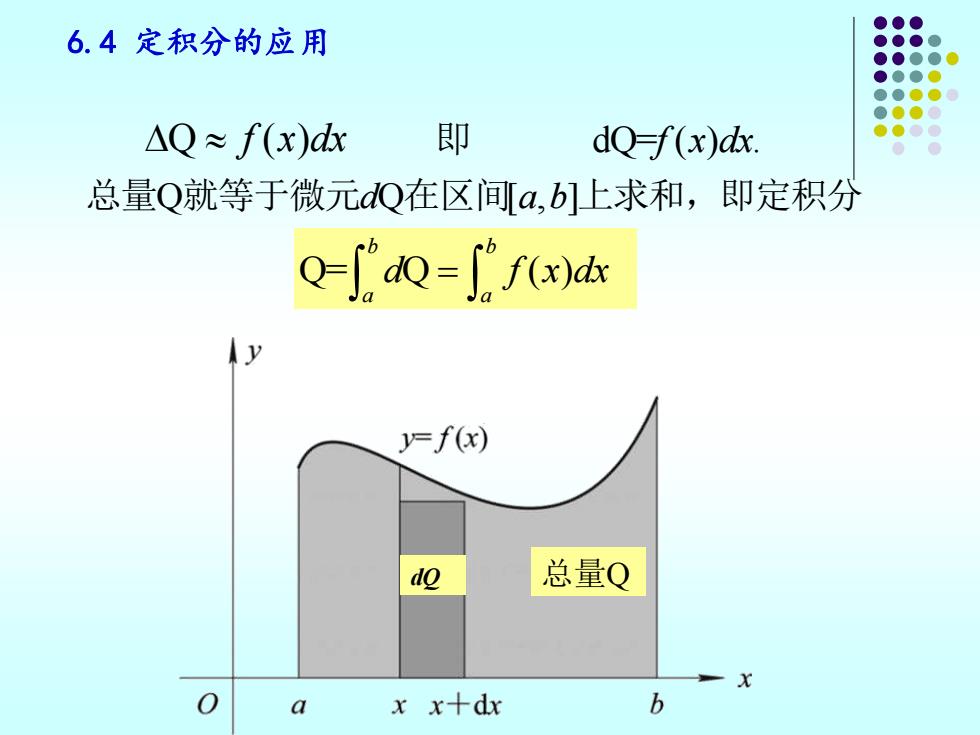
6.4定积分的应用 △Q≈f(x)dx 即 dQ-f(x)dx. 总量Q就等于微元dQ在区间[a,b]上求和,即定积分 Q-∫d0=ifx)ds y=f(x) do 总量Q a xx+dx b
6.4 定积分的应用 Q ( ) f x dx 即 dQ= ( ) . f x dx 总量Q Q [ , ] 就等于微元d a b 在区间 上求和,即定积分 Q= Q ( ) b b a a d f x dx = dQ 总量Q
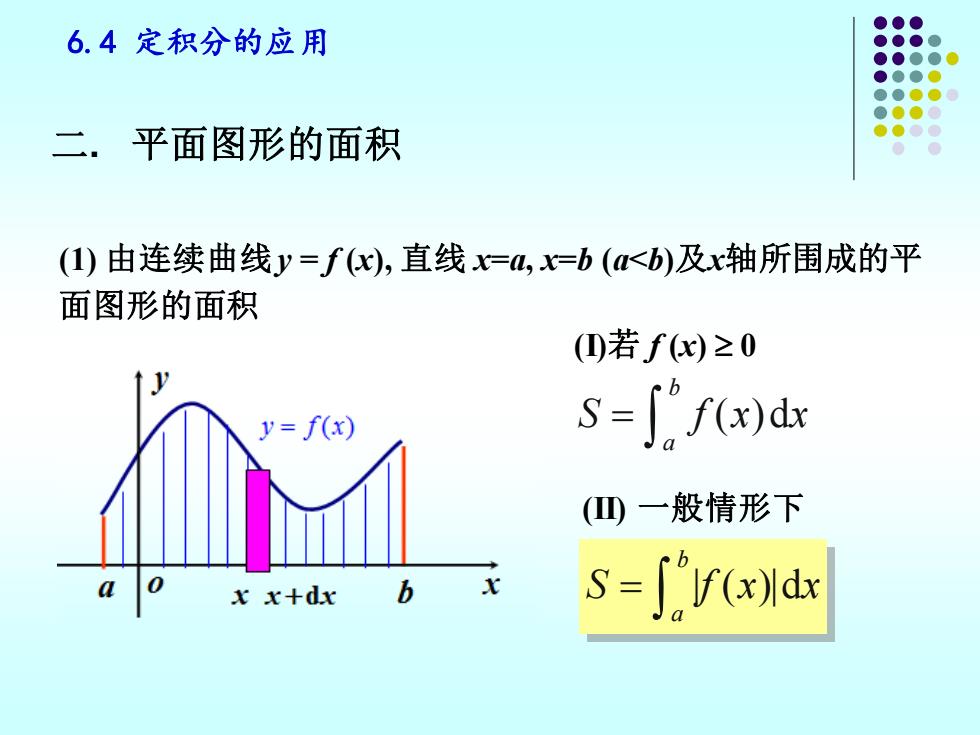
6.4定积分的应用 二.平面图形的面积 (1)由连续曲线y=fx),直线x=a,=b(<b)及x轴所围成的平 面图形的面积 (①若fx)≥0 y=f(x) S=∫f(x)dx (四一般情形下 xx+dx b S=∫fxd
6.4 定积分的应用 二. 平面图形的面积 (1) 由连续曲线y = f (x), 直线 x=a, x=b (a<b)及x轴所围成的平 面图形的面积 ( )d b a S f x x = (I)若 f (x) 0 | ( )|d b a S f x x = (II) 一般情形下
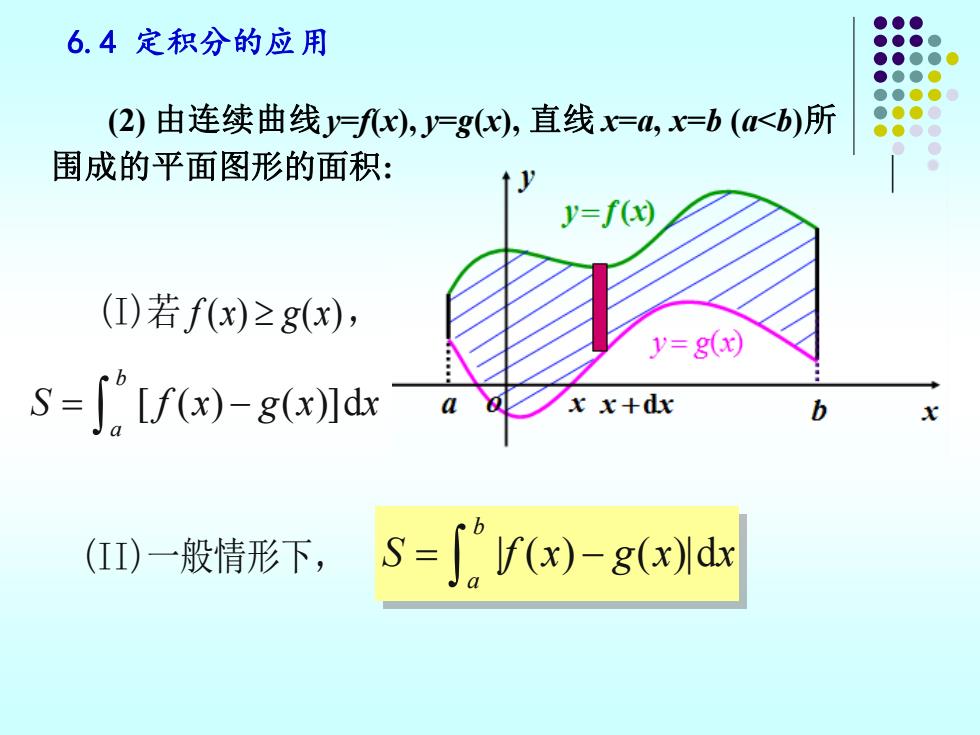
6.4定积分的应用 (2)由连续曲线y=f),J=gc),直线=,x=b(<b)所 围成的平面图形的面积: Y=f(x) (I)若f(x)≥g(x), y=g(x) S=∫[f(x)-g(x]dr a xx+dx b (II)一般情形下, S=f(x)-g(x)ldx
6.4 定积分的应用 (I)若 f x g x ( ) ( ) , (2) 由连续曲线y=f(x), y=g(x), 直线 x=a, x=b (a<b)所 围成的平面图形的面积: [ ( ) ( )]d b a S f x g x x = − (II)一般情形下, | ( ) ( )|d b a S f x g x x = −

6.4定积分的应用 例题1 求由正弦曲线y=sinx和直线y=0,x=0及x= 3π 2 所围图形的面积. 解: 3π s=∫02 Isinx=j0sink-∫r2s sin xdx 3元 =-C0sx16+c0sx|z2=3
6.4 定积分的应用 例题1 3 sin 0, 0 2 y x y x x 求由正弦曲线 = = = = 和直线 及 所围图形的面积. 3 3 2 2 0 0 S x dx xdx xdx | sin | sin sin = = − 解: 3 2 0 cos | cos | 3 x x = − + =
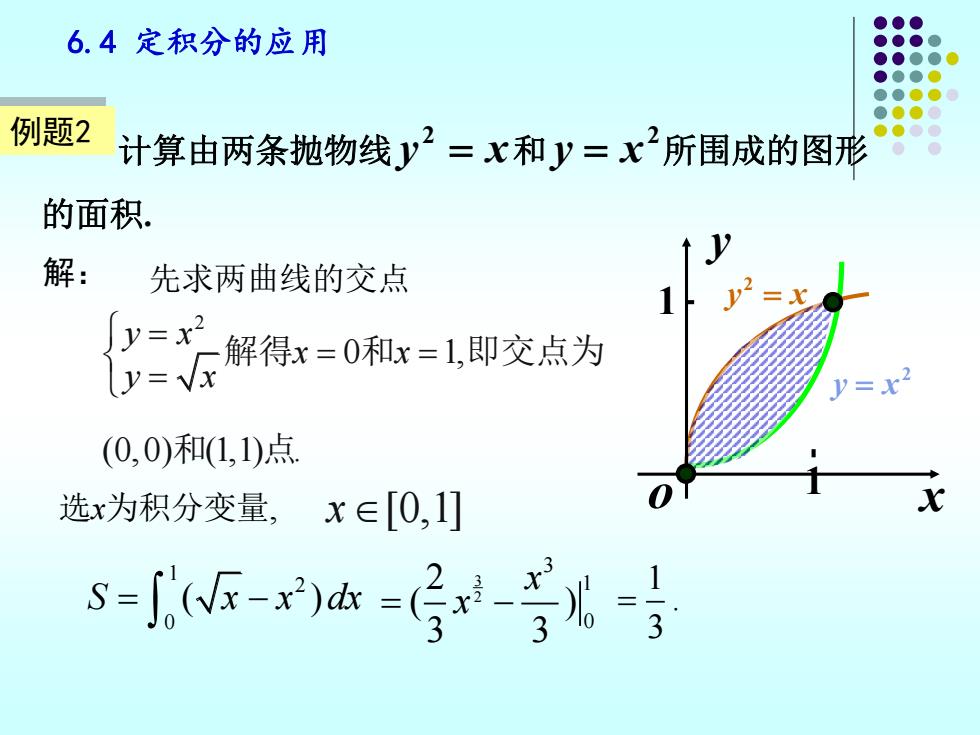
6.4定积分的应用 例题2 计算由两条抛物线y2=x和y=x2所围成的图形 的面积. 解: 先求两曲线的交点 解得x=0和x=1,即交点为 (0,0)和(1,1)点 选x为积分变量,x∈[0,1] s-G-r-后x-等0-月
6.4 定积分的应用 计算由两条抛物线 y = x 2 和 2 y = x 所围成的图形 的面积. 解: 先求两曲线的交点 2 0 1, (0,0) (1,1) . y x x x y x = = = = 解得 和 即交点为 和 点 选x为积分变量, x[0,1] 1 2 0 S x x dx = − ( ) 3 2 3 1 0 2 ( ) 3 3 x = − x 1 . 3 = 例题2 1 2 y = x x y o y = x 2 1
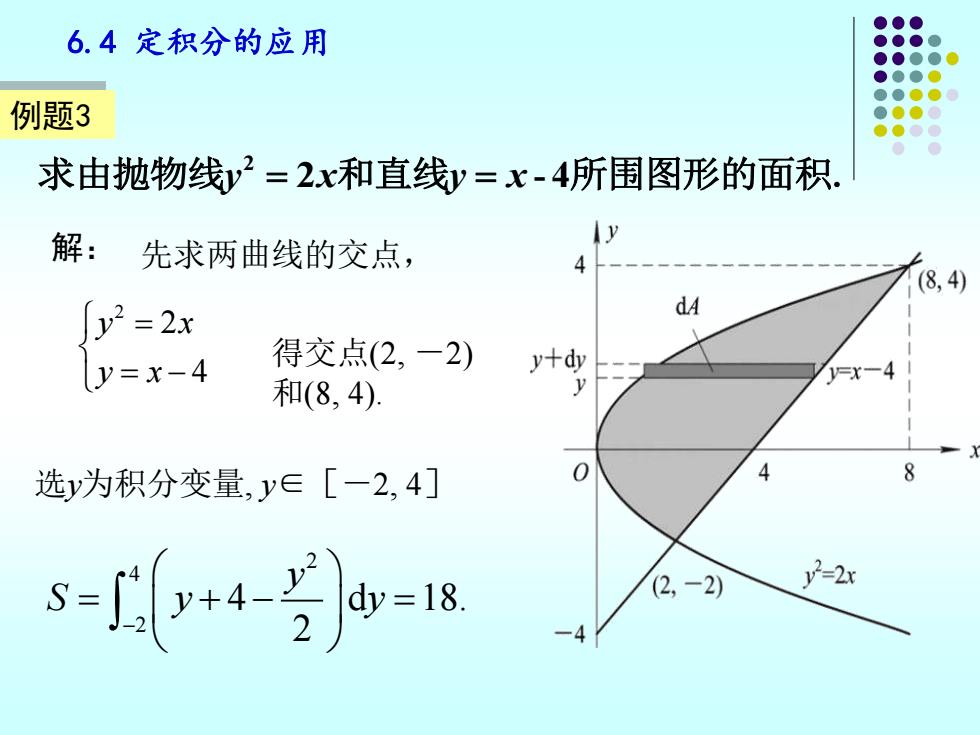
6.4定积分的应用 例题3 求由抛物线y2=2x和直线y=x-4所围图形的面积. 解: 先求两曲线的交点, (8, y2=2x dA y=x-4 得交点(2,-2) y+dy =x-4 和(8,4) 选y为积分变量,y∈[一2,4] 0 s-〔45=18 (2,-2) y2=2x
6.4 定积分的应用 例题3 2 求由抛物线y x y x = = 2 - 4 和直线 所围图形的面积. = − = 4 2 2 y x y x 得交点(2, -2) 和(8, 4). 解: 先求两曲线的交点, 选y为积分变量, y∈[-2, 4] 2 4 2 4 d 18. 2 y S y y − = + − =
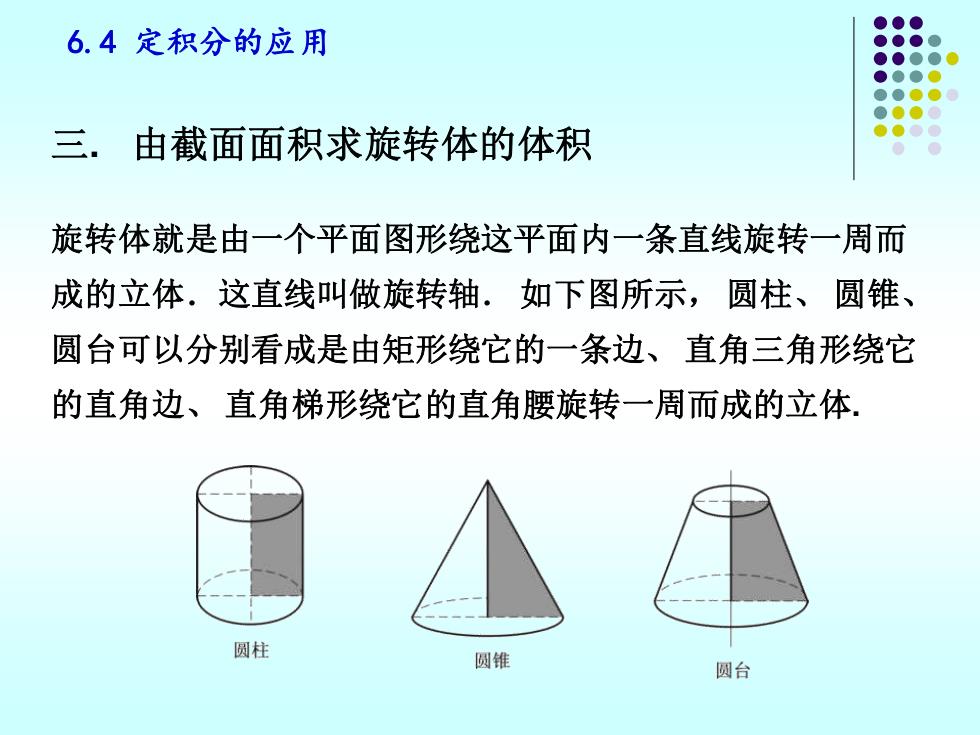
6.4定积分的应用 三.由截面面积求旋转体的体积 旋转体就是由一个平面图形绕这平面内一条直线旋转一周而 成的立体.这直线叫做旋转轴.如下图所示,圆柱、圆锥、 圆台可以分别看成是由矩形绕它的一条边、直角三角形绕它 的直角边、直角梯形绕它的直角腰旋转一周而成的立体. 圆柱 圆锥 圆台
6.4 定积分的应用 旋转体就是由一个平面图形绕这平面内一条直线旋转一周而 成的立体.这直线叫做旋转轴. 如下图所示, 圆柱、 圆锥、 圆台可以分别看成是由矩形绕它的一条边、 直角三角形绕它 的直角边、 直角梯形绕它的直角腰旋转一周而成的立体. 三. 由截面面积求旋转体的体积
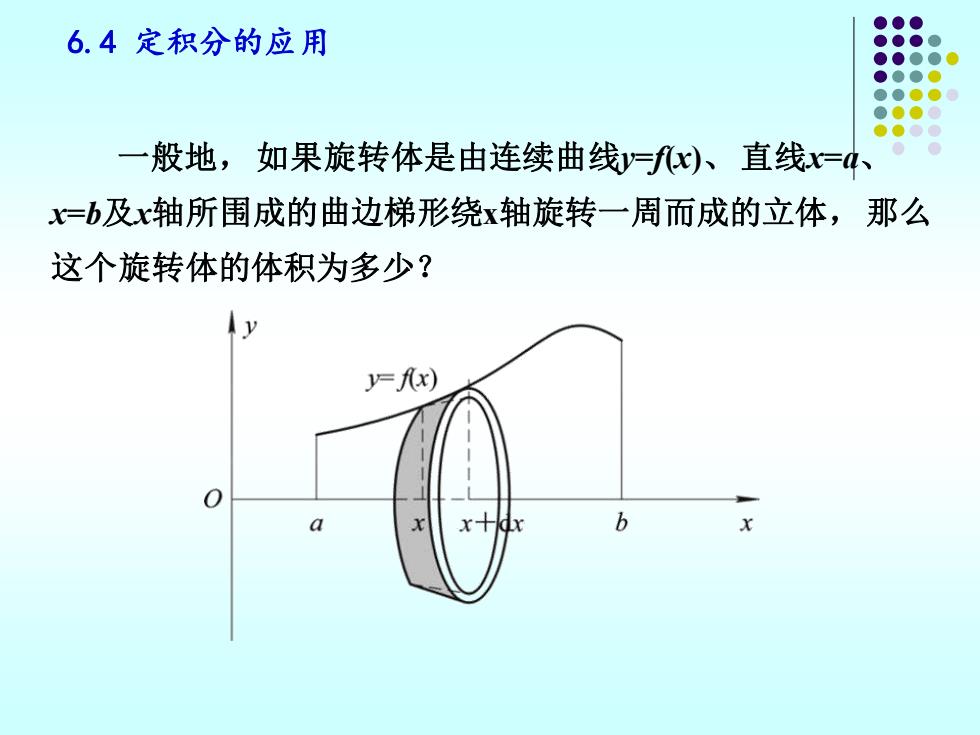
6.4定积分的应用 一般地,如果旋转体是由连续曲线y=fx)、直线=、 =b及x轴所围成的曲边梯形绕x轴旋转一周而成的立体,那么 这个旋转体的体积为多少? =x) b
6.4 定积分的应用 一般地,如果旋转体是由连续曲线y=f(x)、直线x=a、 x=b及x轴所围成的曲边梯形绕x轴旋转一周而成的立体,那么 这个旋转体的体积为多少?