
数学模型方法 Mathematical Modeling Method
数学模型方法 Mathematical Modeling Method
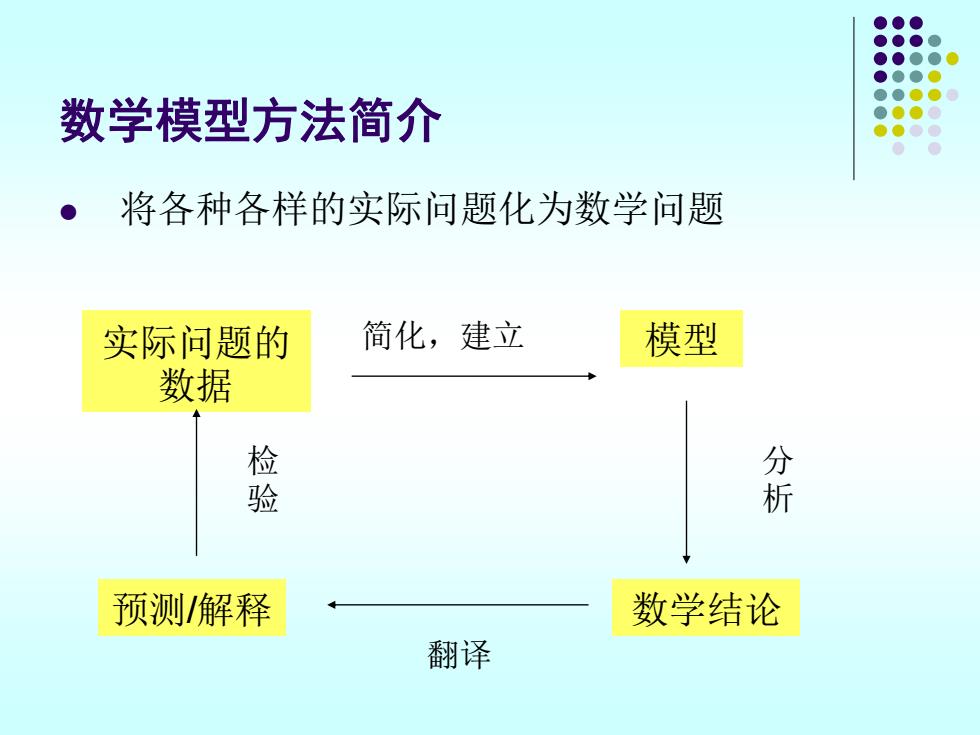
数学模型方法简介 ·将各种各样的实际问题化为数学问题 实际问题的 简化,建立 模型 数据 检 分 预测/解释 数学结论 翻译
数学模型方法简介 ⚫ 将各种各样的实际问题化为数学问题 实际问题的 数据 模型 预测/解释 数学结论 简化,建立 翻译 分 析 检 验

数学模型方法简介 构建数学模型的步骤和方法 (1)识别问题,确定变量与常量; (2)采用数学符号,建立自变量和应变量以及常 量之间的关系一数学模型; (3)在模型上进行必要的逻辑推理和演算,求得 模型的解答 (4)返回到实际问题中进行检验!
构建数学模型的步骤和方法 数学模型方法简介 (1) 识别问题,确定变量与常量; (2) 采用数学符号,建立自变量和应变量以及常 量之间的关系——数学模型; (3) 在模型上进行必要的逻辑推理和演算,求得 模型的解答 (4) 返回到实际问题中进行检验

数学模型方法举例 。例1.单利与复利模型 单利:设P是本金,为计息期的利率,n是计息 期数,I是n个计息期应付的单利,p为本利和. 单利模型: p=Po+l=Po+Porn=po(1+rn)
数学模型方法举例 ⚫ 例1. 单利与复利模型 单利: 设 是本金,r为计息期的利率,n是计息 期数,I是n个计息期应付的单利,p为本利和. 单利模型: 0 p p p I p p rn p rn = = + = + 0 0 0 0 + (1 )

数学模型方法举例 。例1.单利与复利模型 复利:设Po是本金,为单位计息期的利率,是 计息期数,如果每期结算一次,即前一期结束 的本利和作为下一期的本金,p为本利和. 复利模型: P=Po+Por=Po(1+r) P2=P+Pr=P(1+r)+P(1+r)r=p(1+r)2 P,=p(1+r)
数学模型方法举例 ⚫ 例1. 单利与复利模型 复利:设 是本金,r为单位计息期的利率,t是 计息期数,如果每期结算一次,即前一期结束 的本利和作为下一期的本金,p为本利和. 0 p 1 0 0 0 2 2 1 1 0 0 0 0 (1 ) (1 ) (1 ) (1 ) . (1 )t t p p p r p r p p p r p r p r r p r p p r = + = + = + = + + + = + = + 复利模型:

数学模型方法举例 如果单利和复利以相同的利率来计算,显然复利 模型的本利和要大于单利模型的本利和 。以年利率3.25%为例 计息期 单利(3.25%)本利和 复利(3.25%)本利和 第1年 10000×(1+0.0325) 10000×(1+0.0325) 第2年 10000×(1+0.065) 10325×(1+0.0325) 第3年 10000×(1+0.0975)=10975 10661×(1+0.0325)=11007 aaaaaa 第10年 13250 13769
数学模型方法举例 ⚫ 如果单利和复利以相同的利率来计算,显然复利 模型的本利和要大于单利模型的本利和. ⚫ 以年利率3.25%为例 计息期 单利(3.25%)本利和 复利(3.25%)本利和 第1年 10000×(1+0.0325) 10000×(1+0.0325) 第2年 10000×(1+0.065) 10325×(1+0.0325) 第3年 10000×(1+0.0975)=10975 10661×(1+0.0325)=11007 . . 第10年 13250 13769

数学模型方法举例 ·续例1 如果每期结算m次,那么每一新计息期的利率为m 这样一个原单位计息期就变成m个计息期,原计息期 数变成了mt个计息期,先将每一个新计息期结算的 本利和都作为下一个新计息期的本金,那么原t期后 的本利和为 Pm=Po(1+)w m 问题:1.趋向于无穷大,是否本利和也是趋向于无穷大? 由特殊极限:1im1+)'=e.本利和Pm→p,e” 00
数学模型方法举例 ⚫ 续例1 如果每期结算m次,那么每一新计息期的利率为 , 这样一个原单位计息期就变成m个计息期,原计息期 数t变成了 mt个计息期,先将每一个新计息期结算的 本利和都作为下一个新计息期的本金,那么原t期后 的本利和为 r m 0 (1 )mt mt r p p m = + 问题:1. m趋向于无穷大,是否本利和也是趋向于无穷大? 1 lim(1 ) . x x e → x 由特殊极限: + = 本利和 0 rt mt p p e →

数学模型方法举例 ● 实际问题:某人存入银行1万元,定期一年的年利率为 3.25%,定期三年的年利率为4.25%,问若存3年,怎 样存得到的本利和最多? 计息期 单利(4.25%)本利和 复利(3.25%)本利和 第一年 10000×(1+0.0425) 10000×(1+0.0325) 第二年 10000×(1+0.085) 10325×(1+0.0325) 第三年 10000×(1+0.1275) 10661×(1+0.0325) 11275 11007
数学模型方法举例 ⚫ 实际问题:某人存入银行1万元,定期一年的年利率为 3.25%,定期三年的年利率为4.25%,问若存3年,怎 样存得到的本利和最多? 计息期 单利(4.25%)本利和 复利(3.25%)本利和 第一年 10000×(1+0.0425) 10000×(1+0.0325) 第二年 10000×(1+0.085) 10325×(1+0.0325) 第三年 10000×(1+0.1275) 10661×(1+0.0325) 11275 11007
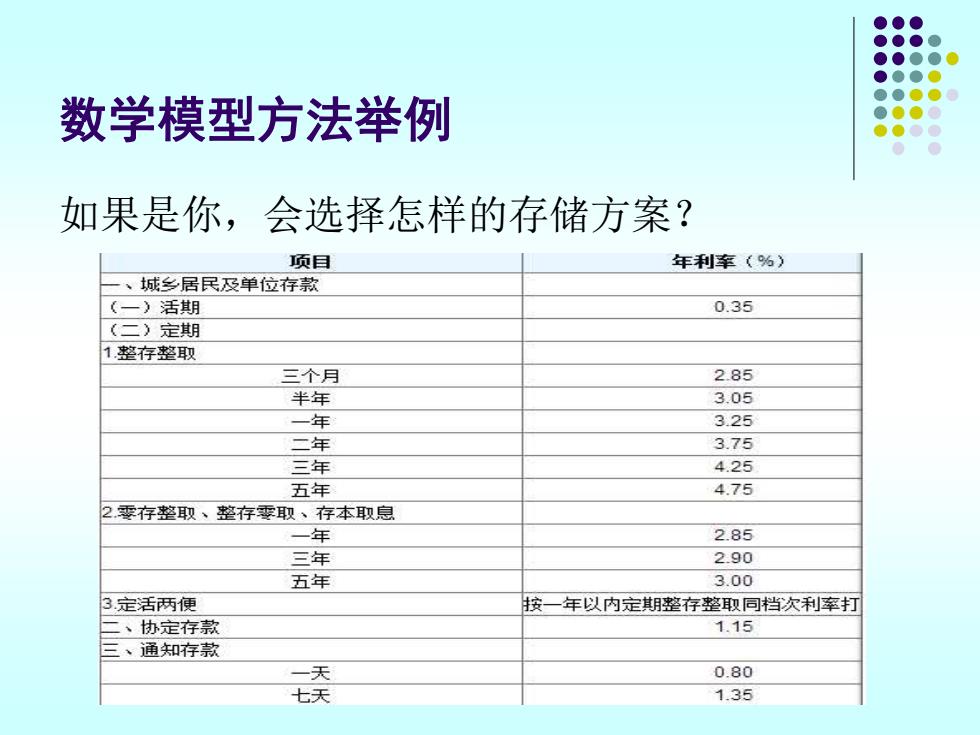
数学模型方法举例 如果是你,会选择怎样的存储方案? 项目 年利率(%) 、城乡居民及单位存款 (一)活期 0.35 (二)定期 1整存整取 三个月 285 半年 3.05 一年 3.25 二年 3.75 三年 4.25 五年 4.75 2零存整取、整存零取、存本取息 一年 2.85 三年 2.90 五年 3.00 3定活两便 按一年以内定期整存整取同档次利率打 二、协定存款 1.15 三、通知存款 一天 0.80 七天 1.35
数学模型方法举例 如果是你,会选择怎样的存储方案?

数学模型方法举例 例2:人口模型 设某地某年人口为P,人口自然增长率 为r,则t年后的人口p为 p=p(1+r) 模型的提出者为马尔萨斯(Mathus, 英)。这一模型适用于生物种群 (人口、细菌、鱼类等)的生存环 境较宽松的情况。但是,当生物种 群数量增长到一定值时,恶化的生 态环境将影响生物种群数量的增长, 这一模型便需要改进。 马尔萨斯(1766-1834)
数学模型方法举例 ⚫ 例2:人口模型 设某地某年人口为 ,人口自然增长率 为r, 则t年后的人口p为 0 p 0 (1 )t p p r = + 模型的提出者为马尔萨斯(Mathus, 英)。这一模型适用于生物种群 (人口、细菌、鱼类等)的生存环 境较宽松的情况。但是,当生物种 群数量增长到一定值时,恶化的生 态环境将影响生物种群数量的增长, 这一模型便需要改进。 马尔萨斯(1766-1834)