
第三章导数与微分
第三章 导数与微分

第三章导数与微分 ■§3.1导数的概念 ■§3.2求导的公式与法则 ■§3.3微分及其运算
第三章 导数与微分 ◼ §3.1 导数的概念 ◼ §3.2 求导的公式与法则 ◼ §3.3 微分及其运算

3.1导数的概念 一.抽象导数概念的两个原型 问题提出 我们在解决实际问题时,除了需要了解变量之间的函数关系以 外,有时还需要研究变量变化快慢的程度.15世纪之后,大量 实际问题给数学提出了亟待解决的新课题。 三类问题 1:求变速运动的瞬时速度 2:求曲线上一点处的切线 3:求极大值和极小值
一. 抽象导数概念的两个原型 3.1 导数的概念 我们在解决实际问题时,除了需要了解变量之间的函数关系以 外,有时还需要研究变量变化快慢的程度. 15世纪之后,大量 实际问题给数学提出了亟待解决的新课题。 问题提出 三类问题 1:求变速运动的瞬时速度 2:求曲线上一点处的切线 3:求极大值和极小值

3.1导数的概念 原型I求变速直线运动的瞬时速度, 设s=f(t)在0,T]上连续,求v=v(t)· 1.提出问题 匀速运动:平均速度口= △S △t 变速运动:瞬时速度 o=? △t>0 想一想如何处理速度变与不变的矛盾?
原型Ⅰ 求变速直线运动的瞬时速度. 匀速运动: 设 s = f (t) 在[0,T]上连续,求 ( ) . 0 v = v t M M0 M1 P △ s O s 平均速度 s v t = 变速运动: 瞬时速度 0 v = ? 1. 提出问题 想一想 如何处理速度变与不变的矛盾? 3.1 导数的概念 →t 0

3.1导数的概念 原型I求变速直线运动的瞬时速度. M ①求增量 0 给t。一个增量△t,对应的路程△s=f(t。+△)-f(t) ②求增量比(局部以匀速代变速) As_f(+△t)-f(t) =A △t △t ③取极限 As =lim A.S vo lim=lim f(t。+△t)-f(t) △t→>0 △t-→0△t 1→0 △t
①求增量 0 0 0 给t t s f t t f t 一个增量 , ( ) - ( ) 对应的路程 = + ②求增量比(局部以匀速代变速) t f t t f t t s v + − = = ( ) ( ) 0 0 ③ 取极限 t f t t f t t s v v t t t + − = = = → → → ( ) ( ) lim lim lim 0 0 0 0 0 0 原型Ⅰ 求变速直线运动的瞬时速度. 3.1 导数的概念 M M0 M1 P △ s O s
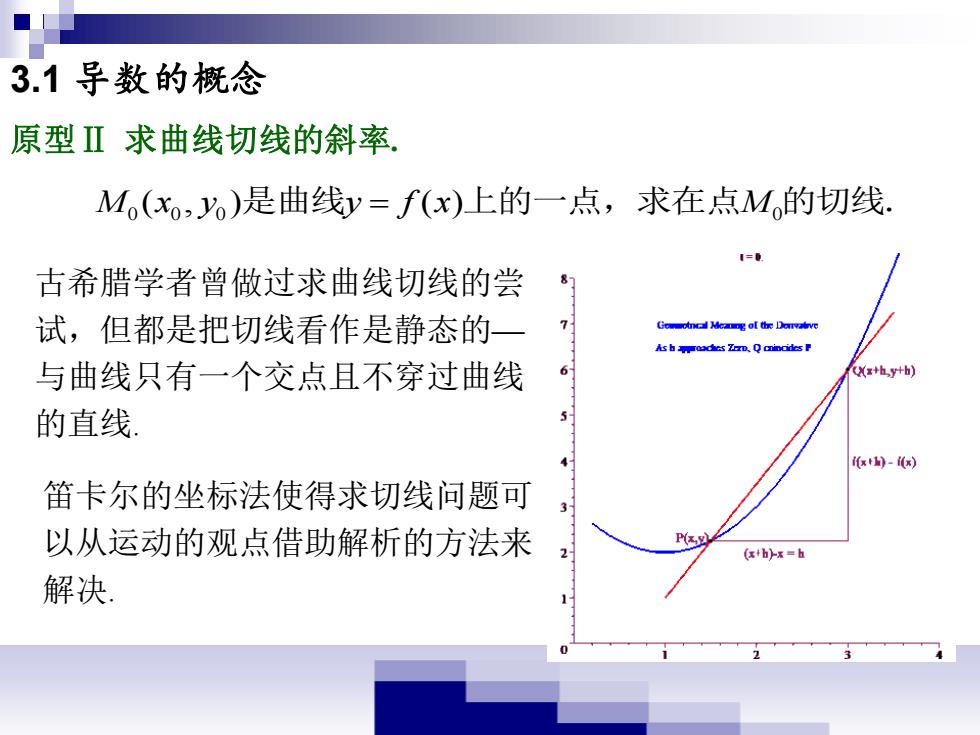
3.1导数的概念 原型Ⅱ求曲线切线的斜率 Mo(x,)是曲线y=f(x)上的一点,求在点M的切线. 1=0 古希腊学者曾做过求曲线切线的尝 试,但都是把切线看作是静态的 与曲线只有一个交点且不穿过曲线 Xx+hy+b) 的直线 x山-(x) 笛卡尔的坐标法使得求切线问题可 以从运动的观点借助解析的方法来 (x+h)x=h 解决
原型Ⅱ 求曲线切线的斜率. 0 0 0 0 M x y y f x M ( , ) ( ) 是曲线 = 上的一点,求在点 的切线. 古希腊学者曾做过求曲线切线的尝 试,但都是把切线看作是静态的— 与曲线只有一个交点且不穿过曲线 的直线. 3.1 导数的概念 笛卡尔的坐标法使得求切线问题可 以从运动的观点借助解析的方法来 解决
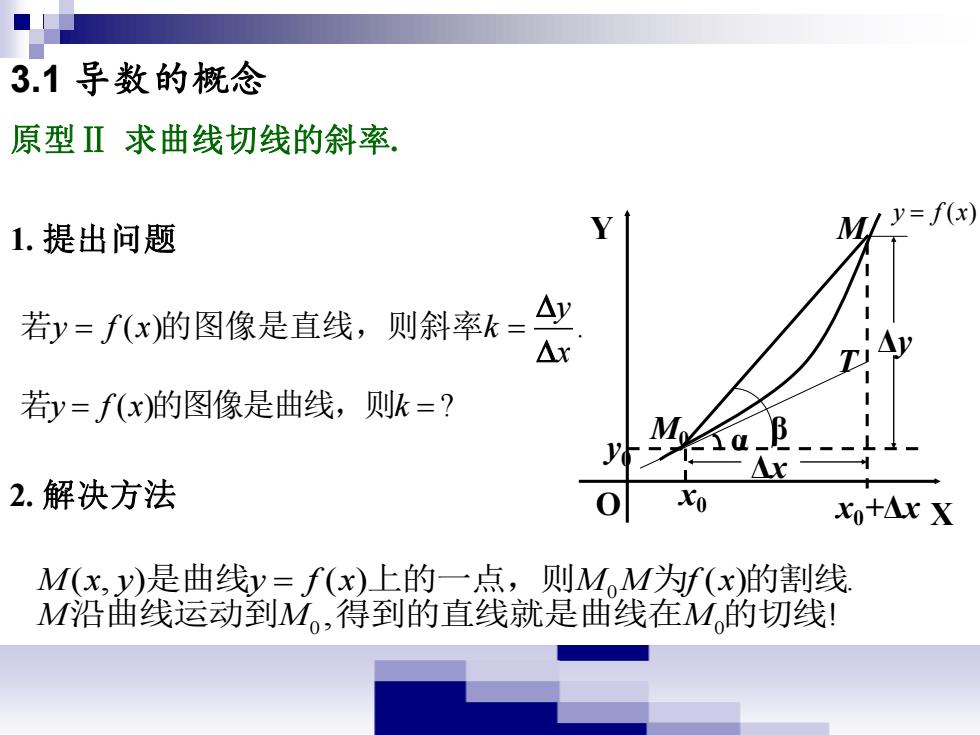
3.1导数的概念 原型Ⅱ求曲线切线的斜率 1.提出问题 Y M/ y=f(x) 若y=f(x)的图像是直线,则斜率k= △y △x 若y=f(x)的图像是曲线,则k=? 2.解决方法 x+△xX M(x,y)是曲线y=f(x)上的一点,则MM为f(x)的割线 M沿曲线运动到M,得到的直线就是曲线在M的切线划
1. 提出问题 ( ) . 若 的图像是直线,则斜率 y y f x k x = = 若y f x k = = ( ) ? 的图像是曲线,则 O X Y Δx M0 M Δy y0 x0 x0+Δx T α y = f (x) β 原型Ⅱ 求曲线切线的斜率. 3.1 导数的概念 2. 解决方法 0 0 0 ( , ) ( ) ( ) . , ! 是曲线 上的一点,则 为 的割线 沿曲线运动到 得到的直线就是曲线在 的切线 M x y y f x M M f x M M M =
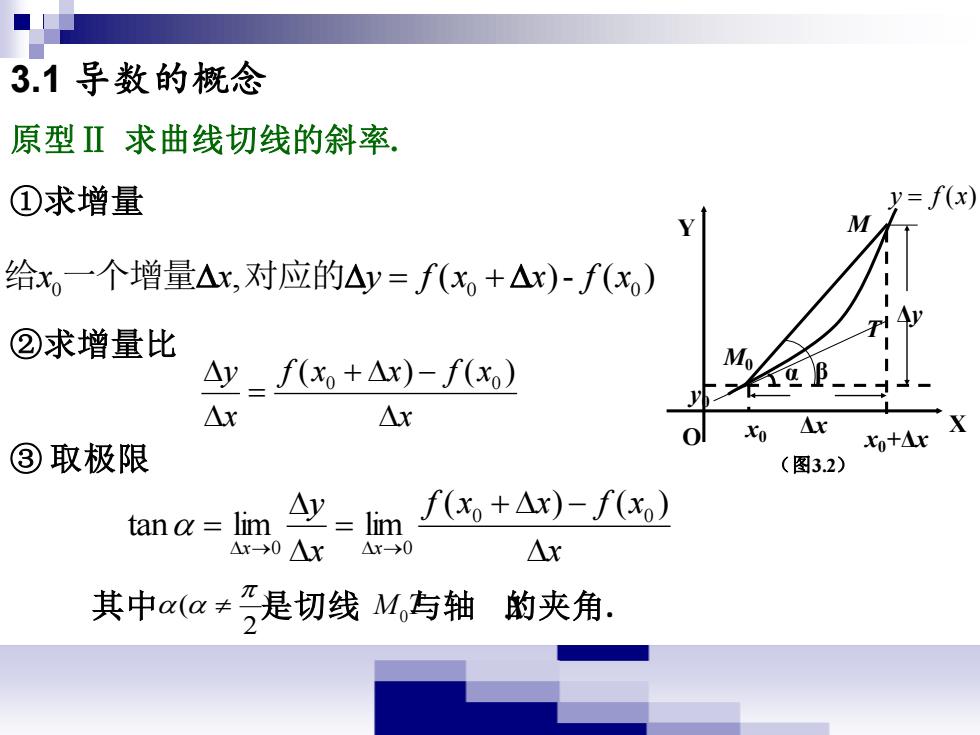
3.1导数的概念 原型Ⅱ求曲线切线的斜率 ①求增量 y=f(x) Y M 给x。一个增量△x,对应的△y=f(x,+△x)-f(x)》 ②求增量比 △y_f(x+Ax)-f(x) M △x △x ③取极限 xo+△x (图3.2) tana=lim Ay=lim f(x+△x)-f(x) Ar0△x △x 其中a(a≠是切线M,与轴 的夹角
①求增量 ②求增量比 x f x x f x x y + − = ( ) ( ) 0 0 ③ 取极限 x f x x f x x y x x + − = = → → ( ) ( ) tan lim lim 0 0 0 0 其中 是切线 ) 与轴 的夹角. 2 ( M0 T x O X Y Δx M0 M Δy y0 x0 x0+Δx T α y = f (x) β (图3.2) 0 0 0 给x x y f x x f x 一个增量 , ( ) - ( ) 对应的 = + 原型Ⅱ 求曲线切线的斜率. 3.1 导数的概念

3.1导数的概念 原型I求变速直线运动的瞬时速度, 总结 原型Ⅱ求曲线切线的斜率. 上面两个现实原型的范畴虽不相同,但从纯数学的角度来 考察,所要解决的问题相同:求一个变量相对于另一个相 关变量的变化快慢程度,即变化率问题 处理问题的思想方法相同;矛盾转化的辨证方法; 数学结构相同:函数改变量与自变量改变之比,当自变量 改变量趋于零时的极限. 由这两个具体问题便可抽象出导数的概念
上面两个现实原型的范畴虽不相同,但从纯数学的角度来 考察,所要解决的问题相同:求一个变量相对于另一个相 关变量的变化快慢程度,即变化率问题; 3.1 导数的概念 处理问题的思想方法相同;矛盾转化的辨证方法; 数学结构相同:函数改变量与自变量改变之比,当自变量 改变量趋于零时的极限. 由这两个具体问题便可抽象出导数的概念。 总结 原型Ⅰ 求变速直线运动的瞬时速度. 原型Ⅱ 求曲线切线的斜率

3.1导数的概念 二.导数的概念 定义设y=f(x)在点x的某一邻域内有定义,当 自变量x在x,处有增量△(x。+△x仍在该邻域内),对 应的函数增量△y=f(x。+△x)-f(x)当△x→0时, 若少的极限存在, 则称这个极限值为函数y=f(x) ▲X 在点x处的导数, 记作y即y= Ay lim f(x,+△x)-f(x,) △r→0△x △x 一个整体 也可记作 或四 x=X 符号 注意:如果上述极限不存在,则称在该点处不可导
0 0 0 0 0 0 ( ) ( ) ( ) - ( ). 0 ( ) 设 在点 的某一邻域内有定义,当 自变量 在 处有增量 仍在该邻域内,对 应的函数增量 当 时, 若 的极限存在,则称这个极限值为函数 定义 在点 处的导数, y f x x x x x x x y f x x f x x y y x x f x = + = + → = 0 记作 x x y = 0 0 ( ) 也可记作 或 , x x x x dy df x dx dx = = 0 0 0 0 0 ( ) ( ) 即 x x lim lim x x y f x x f x y x x = → → + − = = 注意:如果上述极限不存在,则称在该点处不可导. 一个整体 符号 3.1 导数的概念 二. 导数的概念