
§1.2微积分的研究对象—函数 函数的定义 二 函数的性质 ■三 反函数 ■四.基本初等函数 ■五.复合函数 六. 初等函数
§1.2 微积分的研究对象——函数 ◼ 一. 函数的定义 ◼ 二. 函数的性质 ◼ 三. 反函数 ◼ 四. 基本初等函数 ◼ 五. 复合函数 ◼ 六. 初等函数

一.函数的定义 常量:保持不变的量 变量:可以取不同值的量 笛卡尔(1596-1650) ■法国数学家笛卡尔创立坐标几何 后使变量和函数概念进入数学, ■瑞士数学家欧拉首创了一种用符 号来说“y是x的函数”的方法. 欧拉(1707-1783)
一 . 函数的定义 ◼ 法国数学家笛卡尔创立坐标几何 后使变量和函数概念进入数学. ◼ 瑞士数学家欧拉首创了一种用符 号来说“ y 是 x 的函数”的方法. 常量:保持不变的量 变量:可以取不同值的量 笛卡尔(1596-1650) 欧拉(1707-1783)

一.函数的定义 函数是用数学术语来描述现实世界的主要工具 1.定义:如果在某个变化过程中有两个变量x,y 并且对于x在某个变化范围X内的每一个确定的值, 按照某个对应法则测f,y都有唯一确定的值和它对 应,y就是x的函数,记作 y=f(x) x为自变量,X是f的定义域,y为因变量,全体函 数值的集合Y称作函数的值域, X→Y
一 . 函数的定义 函数是用数学术语来描述现实世界的主要工具 1. 定义:如果在某个变化过程中有两个变量 x, y, 并且对于 x 在某个变化范围X内的每一个确定的值, 按照某个对应法则 f ,y都有唯一确定的值和它对 应,y 就是 x 的函数,记作 y f x = ( ) x 为自变量, X 是 f 的定义域, y为因变量,全体函 数值的集合Y称作函数的值域. f X Y ⎯⎯→
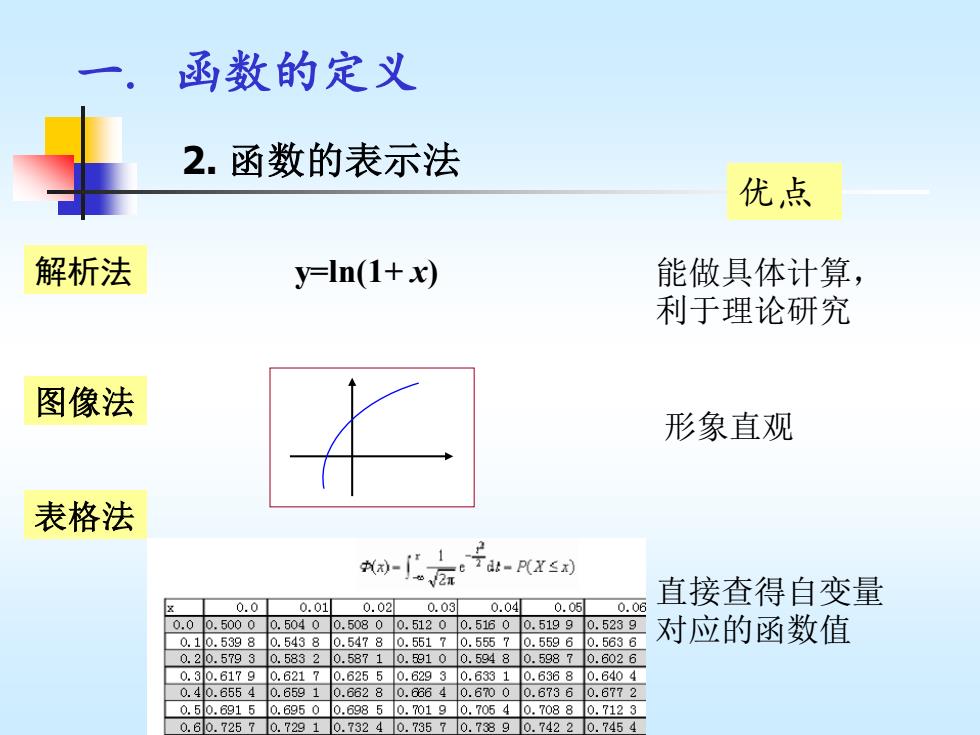
函数的定义 2.函数的表示法 优点 解析法 y=In(1+x) 能做具体计算, 利于理论研究 图像法 形象直观 表格法 直接查得自变量 0.0 0.01 0.020.030.04 0.05 0.06 0.0 0.50000.50400.50800.51200.51600.51990.5239 0.10.53980.54380.54780.55170.5570.55960.5636 对应的函数值 0.20.5793 0.5832 0.58710.59100.59480.5987 0.6026 0.30.6179 0.6217 0.62550.62930.63310.63680.6404 0.40.6554 0.6591 0.66280.66640.67000.67360.6772 0.50.69150.69500.69850.70190.70540.70880.7123 0.60.72570.729 1 0.73240.73570.73890.74220.7454
一 . 函数的定义 2. 函数的表示法 解析法 图像法 表格法 y=ln(1+ x) 优点 直接查得自变量 对应的函数值 形象直观 能做具体计算, 利于理论研究
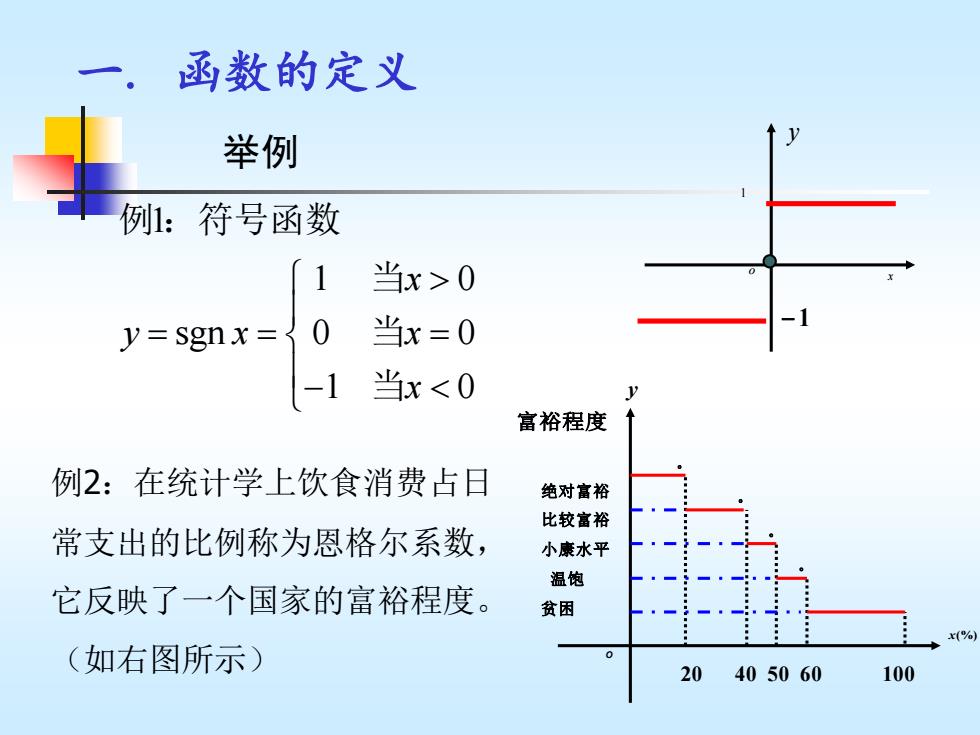
一.函数的定义 举例 例1:符号函数 1 当x>0 y=sgnx= 0 当x=0 -1 当x<0 富裕程度 例2:在统计学上饮食消费占日 绝对富裕 比较富裕 常支出的比例称为恩格尔系数, 小康水平 温饱 它反映了一个国家的富裕程度。 贫困 r(%) (如右图所示) 20 405060 100
一 . 函数的定义 举例 1 1 0 sgn 0 0 1 0 x y x x x = = = − 例 :符号函数 当 当 当 x y o − 1 1 x(%) 20 40 50 60 100 绝对富裕 比较富裕 小康水平 温饱 贫困 。 。 。 。 y 富裕程度 O 例2:在统计学上饮食消费占日 常支出的比例称为恩格尔系数, 它反映了一个国家的富裕程度。 (如右图所示)

一, 函数的定义 举例 例3:狄利克雷函数(Dirichlet) y=D()= 当x是有理数时 0 当x是无理数时 r=a(1-sin) 例4:极坐标下的心形函数 r=a(1-sin0)
一 . 函数的定义 举例 4 r a= (1 sin ) − 例 :极坐标下的心形函数 例3:狄利克雷函数(Dirichlet) = = 当 是无理数时 当 是有理数时 x x y D x 0 1 ( )
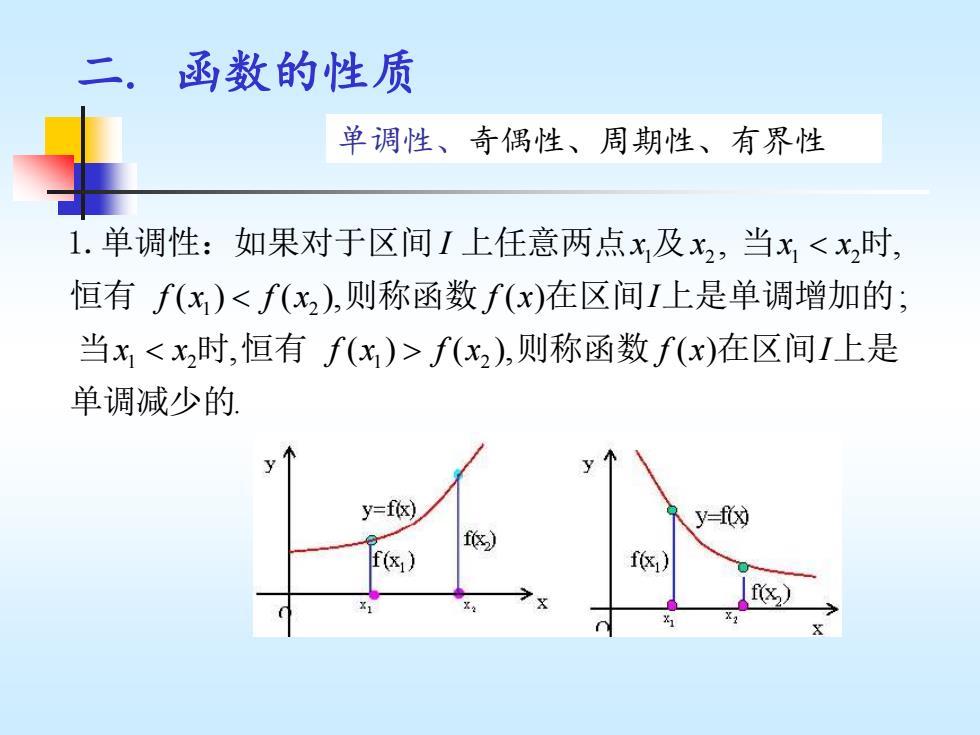
二.函数的性质 单调性、奇偶性、周期性、有界性 1.单调性:如果对于区间I上任意两点x及x2,当xf(x2),则称函数f(x)在区间I上是 单调减少的 y y=fx) y-f(x) f) f(x)
二. 函数的性质 单调性、奇偶性、周期性、有界性 1 2 1 2 1 2 1 2 1 2 , , ( ) ( ), ( ) ; , ( ) ( ), ( ) . I x x x x f x f x f x I x x f x f x f x I 1.单调性:如果对于区间 上任意两点 及 当 时 恒有 则称函数 在区间 上是单调增加的 当 时 恒有 则称函数 在区间 上是 单调减少的

二。函数的性质 单调性、奇偶性、周期性、有界性 2.奇偶性:如果对于x∈D(D为对称区间),有f(-x)=f(x), 则称f(x)为偶函数,若有f(-x)=-f(x),则称f(x)为奇函数 偶函数的图像关于y轴对称,奇函数的图像关于原点对称
二. 函数的性质 ( ), ( ) ( ) ( ) ; ( ) - ( ) ( ) x D D f x f x f x f x f x f x − = − = 2.奇偶性:如果对于 为对称区间 有 , 则称 为偶函数 若有 ,则称 为奇函数. 偶函数的图像关于y轴对称,奇函数的图像关于原点对称. 单调性、奇偶性、周期性、有界性
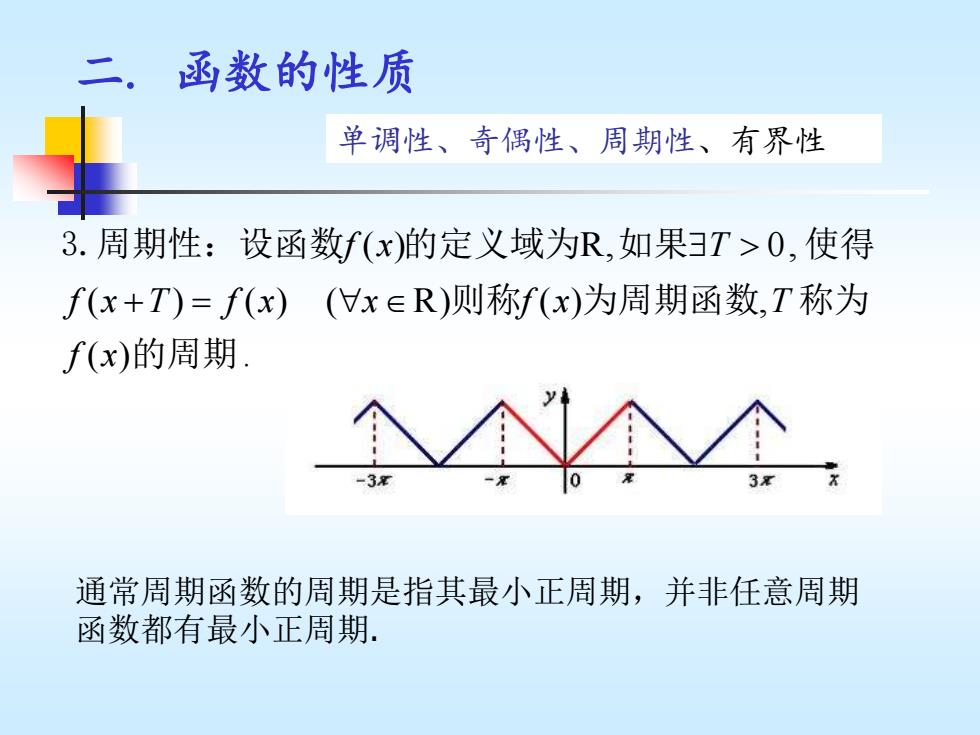
二.函数的性质 单调性、奇偶性、周期性、有界性 3.周期性:设函数f(x)的定义域为R,如果T>0,使得 f(x+T)=f(x)(x∈R)则称f(x)为周期函数,T称为 f(x)的周期. -3 3 通常周期函数的周期是指其最小正周期,并非任意周期 函数都有最小正周期
二. 函数的性质 ( ) R, 0, ( ) ( ) ( R) ( ) , ( ) . f x T f x T f x x f x T f x + = 3.周期性:设函数 的定义域为 如果 使得 则称 为周期函数 称为 的周期 通常周期函数的周期是指其最小正周期,并非任意周期 函数都有最小正周期. 单调性、奇偶性、周期性、有界性
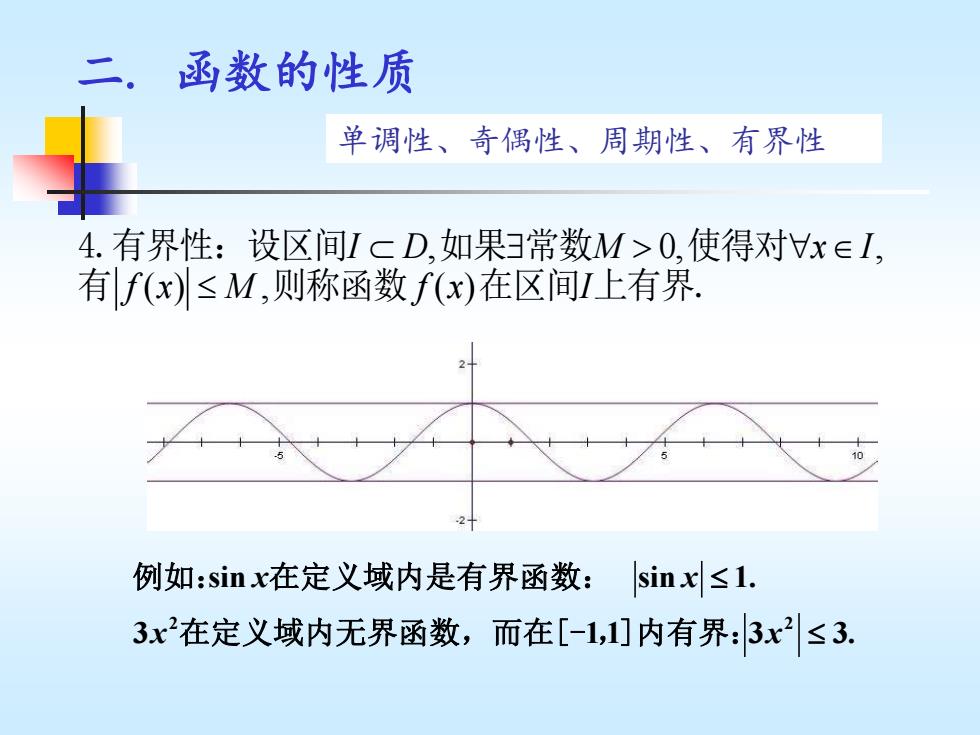
二.函数的性质 单调性、奇偶性、周期性、有界性 4.有界性:设区间IcD,如果常数M>0,使得对Vx∈I, 有f(x)≤M,则称函数f(x)在区间I上有界. 例如:sinx在定义域内是有界函数:sinx≤1. 3x2在定义域内无界函数,而在[-1,1]内有界:3x2≤3
, 0, , ( ) , ( ) I D M x I f x M f x I 4.有界性:设区间 如果 常数 使得对 有 则称函数 在区间 上有界. 二. 函数的性质 2 2 sin sin 1. 3 1 1 3 3. x x x x 例如: 在定义域内是有界函数: 在定义域内无界函数,而在[- ,]内有界: 单调性、奇偶性、周期性、有界性