第、章 空间解析几何与向量代数 §8一1向量及其钱性适算 空间直角坐标系的概念:(见P6的定义) 空间直角坐标系共有八个卦限 王灵下列区回 空间中的任一点M←一有序数组(x,y,z) x,y,z分别称为点M的横,纵,竖坐标。 空间直角坐标系把空间分为八个部分一一称为八卦限。(说明) 点在各卦限的符号为:
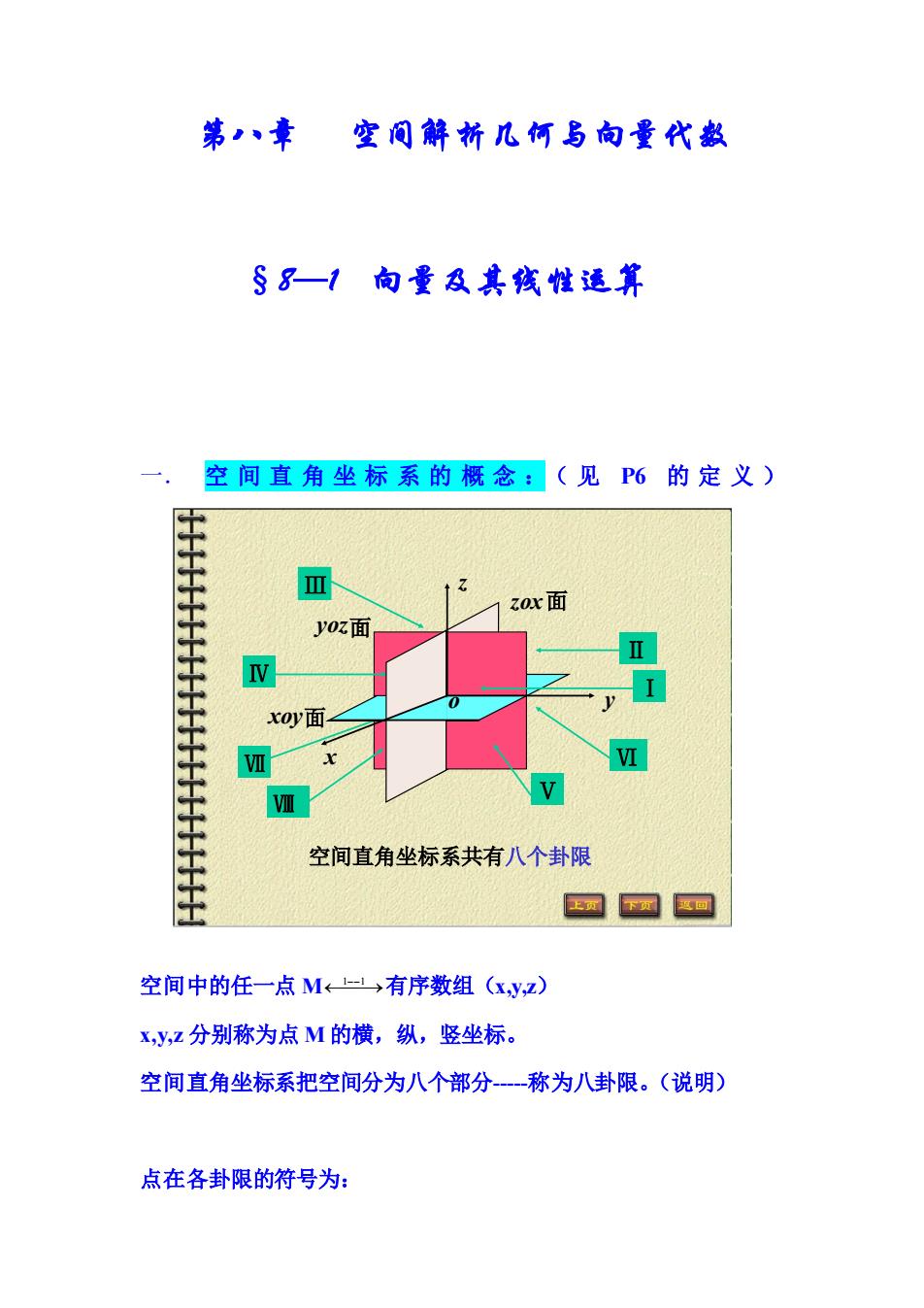
第八章 空间解析几何与向量代数 §8—1 向量及其线性运算 一. 空 间 直 角 坐 标 系 的 概 念 :( 见 P6 的 定 义 ) Ⅶ x o y z xoy面 yoz面 zox面 空间直角坐标系共有八个卦限 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅷ 空间中的任一点 M ⎯⎯→ 1 1 −− 有序数组(x,y,z) x,y,z 分别称为点 M 的横,纵,竖坐标。 空间直角坐标系把空间分为八个部分-称为八卦限。(说明) 点在各卦限的符号为:

卦限(一)Ⅱ(二) .VⅢ(八) (x,y,z)(+,+,+)(-,+,+) . (+,-) 两点距离公式: (数轴上) (平面中) d-x上飞-x d=MM=Vx-x)了+-) dM,M2=Vx2-x)+02-y)2+(52-)月 (空间中) 定比分点公式: 设A(y,)分两点4k,:)为定比:即:4=元,则分点公式 AA、 为 x=考+ y=当+ (中点) 1+元 y=当+ 2 二、向量的概念 1.向量的定义-既有大小,又有方向的量。如:力、速度、 加速度。 2.向量的表示法-一用有向线段表示:ā=4B或坐标表示: a=(a,a2,a3)。 3.向量的模-向量的大小;记为d。 4. 单位向量模为1的向量
卦限 I (一) II(二) . VIII(八) (x,y,z) (+,+,+) (-,+,+) . (+,-,-) 两点距离公式: (数轴上) (平面中) d= ( ) 2 2 1 2 1 | | x x x x − = − d= ( ) ( ) 2 2 1 2 2 1 2 1 | | M M x x y y = − + − d= M1M2 = 2 2 1 2 2 1 2 2 1 (x − x ) + ( y − y ) + (z − z ) (空间中) 定比分点公式: 设 A(x,y,z)分两点 ( , ) i i i, i A x y z 为定比 ;即: 1 2 AA AA = ,则分点公式 为: 1 2 1 2 1 2 1 1 1 x x x y y y z z z + = + + = + + = + (中点) 1 2 1 2 1 2 2 2 2 x x x y y y z z z + = + = + = 二、 向量的概念 1. 向量的定义-既有大小,又有方向的量。如:力、速度、 加速度。 2. 向量的表示法-用有向线段表示: a AB = 或坐标表示: a a a a = ( 1 2 3 , , )。 3. 向量的模-向量的大小; 记为:a 。 4. 单位向量-模为 1 的向量

5.零向量一模为零的向量;记为0。 6.负向量模相等方向相反的向量;的负向量记为-ā。 7.相等的向量-模相等方向相同的向量ā,6:记为a=b。 8.平行(共线)向量-方向相同或相反的向量a,记为a6 三、向量的线性运算 1.向量的加减法 1).向量的加法一一三角形法则,平行四边形法则(如图) a-b 运算律:a+b=i+a a+(6+c=(a+b+c 2).减法—定义:a-i=a+(-b(如图) 且任一向量有a-a=0a+i=a 0-a=-d 2.向量与数量的乘积 1)、定义:数量1与a的乘积定义为一个向量1a。且 1°a=|2a 2°a平行a(2>0时,同向;1<0时,反向;1=0时
5. 零向量-模为零的向量;记为 0。 6. 负向量-模相等方向相反的向量; a a 的负向量记为− 。 7. 相等的向量-模相等方向相同的向量 a b a b , ;记为 = 。 8. 平行(共线)向量-方向相同或相反的向量 a b a b , ; // 记为 。 三、向量的线性运算 1.向量的加减法 1).向量的加法——三角形法则,平行四边形法则 (如图) 运算律: a + b = b + a a + (b + c) = (a + b) + c 2).减法——定义: a −b = a + (−b) (如图) 且任一向量有 a − a = 0 a + 0 = a 0 − a = −a 2. 向量与数量的乘积 1)、定义:数量 与 a 的乘积定义为一个向量 a 。且 1 a = a 2 a 平行 a ( 0 时,同向; 0 时,反向; = 0 时, a b a b − a b +

a=0) 2)、性质1°a平行6(平行、共线)一a=6(1≠0) 2°a=a 3°2ka)=(k)a 41(a+b)=aa+6 S任一非零向量a都可以表示为:aal口哥- (与a同向的单位量ā 可a=cosa,csR,os) 1 (向量的模与方向a分开,给向量的研究带来方便) 例1):证明:任一个三角形的中线可构成一个三角形。 四、向量线性运算的坐标表达 L.向量在轴上的投影 1) 、两个向量的夹角一
a =0 ) 2)、性质 1 a 平行 b (平行、共线) a =b ( 0) 2 a =a 3 (ka)=(k)a 4 (a b a b + = + ) 5 任一非零向量 a 都可以表示为: (与 a 同向的单位量 a 0= {cos ,cos ,cos } | | 1 a = a ) (向量的模与方向 a 分开,给向量的研究带来方便) 例 1):证明:任一个三角形的中线可构成一个三角形。 四 、向量线性运算的坐标表达 1. 向量在轴上的投影 1) 、两个向量的夹角 a 1 2 − a 2a b 0 a a a =| | 0 . | | a a a = a
-两个向量a,万不超过π的夹角p。 2)、投影的定义以及投影的原理: 向量AB在轴1上的投影定义且记为 pri,(AB)=AB=4BIcos 并且Prj,(@,+2++a)=Prj,(a)+.+Prj,(@n) 2.向量的坐标表达式 给出空间一个点M,(x,以,)则向量OM在三个坐标轴上的投影分别 为x,y, 此时向量OM的坐标表达式为: OM=x,y,(或OM=(x,y))x,y:称作OM的坐标 OM的分解表示为:OM=xi+yj+zk 其中i={1,0,0,j={0,1,0,={0,0,1}称为m,y,o轴上的基本单 位向量
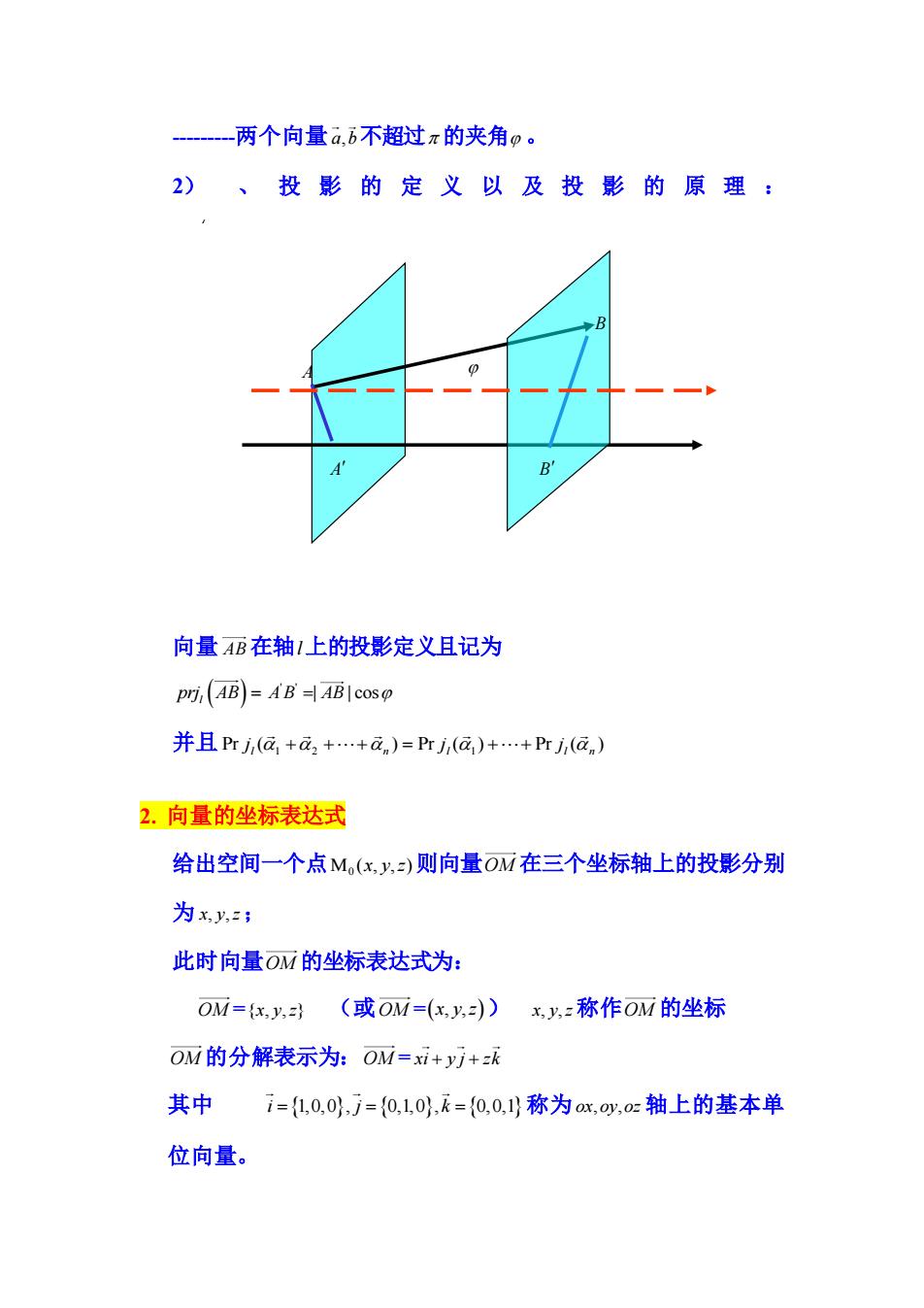
-两个向量 a b, 不超过 的夹角 。 2) 、 投 影 的 定 义 以 及 投 影 的 原 理 : l 向量 AB 在轴 l 上的投影定义且记为 prj AB l ( ) = ' ' A B AB =| | cos 并且 Pr ( ) Pr ( ) Pr ( ) l 1 2 n l 1 l n j j j + + + = + + 2. 向量的坐标表达式 给出空间一个点 ( , , ) 0 x y z 则向量 OM 在三个坐标轴上的投影分别 为 x, y,z ; 此时向量 OM 的坐标表达式为: OM ={x, y,z} (或 OM =( x y z , , ) ) x, y,z 称作 OM 的坐标 OM 的分解表示为: OM = xi y j zk + + 其中 i j k = = = 1,0,0 , 0,1,0 , 0,0,1 称为 ox oy oz , , 轴上的基本单 位向量。 A B A B

(画图分析) 3。向量线性运算的坐标表达 设ā={a,a,a},6=,4,4}则a±i={a±h,a±6,a4±6} ā={a,a2,a,}(1为数量) 给出两点M,(x,y,),i=1,2,则MM={2-x为-片,2-} 五、向量的模与方向余弦的坐标表示法 设任一个向量ā=x,y与x,y:轴的正向夹角为a,B,y(称为方向 角)。而cosa,cosB,cosy称为a的方向余弦,则0≤a,B,y≤π) (模)同=√2+y2+ cosa= Vx2+y2+2 (方向余弦) COs B=- osa.Bys) y coS/= 2+y2+ 与a同向的单位向量为高=acs民小 因此,若已知向量的坐标,则可求出其模和方向余弦,反之,若 知模与方向余弦,则也可求其坐标。 例2):(例一知某一向量的方向与模,求其坐标) 己知a=(2,-3,6),6=(-1,2,-2),向量c与a+6共线,且1ch3W52,求 的坐标。 作业-13页第15题
(画图分析) 3.向量线性运算的坐标表达 设 { , , }, { , , } a = a1 a2 a3 b = b1 b2 b3 则 a b a b a b a b = 1 1 2 2 3 3 , , { , , } a = a1 a2 a3 ( 为数量) 给出两点 ( , , ) i i i i x y z ,i = 1,2 , 则 M M x x y y z z 1 2 2 1 2 1 2 1 = − − − , , 五 、向量的模与方向余弦的坐标表示法 设任一个向量 a = {x, y,z} 与 x, y,z 轴的正向夹角为 , , (称为方向 角)。而 cos,cos ,cos 称为 a 的方向余弦,则 (0 ,, ) (模) 2 2 2 a x y z = + + (方向余弦) 2 2 2 2 2 2 2 2 2 cos cos cos x x y z y x y z z x y z = + + = + + = + + (0 ,, ) 与 a 同向的单位向量为 a 0= {cos ,cos ,cos } | | 1 a = a 。 因此,若已知向量的坐标,则可求出其模和方向余弦,反之,若 知模与方向余弦,则也可求其坐标。 例 2):(例一知某一向量的方向与模,求其坐标) 已知 a b = − = − − (2, 3,6 , 1,2, 2 ) ( ) ,向量 c 与 a b + 共线,且 | | 3 32 c = ,求 c 的坐标。 作业-13 页第 15 题

§8-2数量积、向量积和混合积* 二、两个向量的数量积(点积或内积) 1,点积的定义: 设给出向量a与6,且a与6的夹角为e,称同cose为 a与方的数量积,记为a.i,即a.i=园同cos0 2.点积的性质及运算律: 1)a.a= 2)ii=jj=kk=1 3)1.j=j.k=k.i=0 4)a16a.6=0 5)a.b=b.a 6)2(a-6)=(a6 7)a-(6+d=a-b+a-c 3.点积的坐标表示法 设a={a,a2,a},i=,b2,b} 则a-b=a4+a.h+a6-∑ah 4.几个结论: 由于a-i=abcos=a,4+a,4+a,h因此有: )夹角=云,匠+店+·公+公+ ab+azb2 +asb3 2)a1iea-i=0,即a,b+a,b+a,b=0
§8-2 数量积、向量积和混合积* 一、 两个向量的数量积(点积或内积) 1. 点积的定义: 设给出向量 a 与 b ,且 a 与 b 的夹角为 ,称 a b cos 为 a 与 b 的数量积,记为 a b ,即 a b = a b cos 2. 点积的性质及运算律: 1) a a = 2 a 2) i i j j k k = = =1 3) i j j k k i = = = 0 4) a b a b ⊥ =0 5) a b b a = 6) (a b a b = ) ( ) 7) a b c a b a c + = + ( ) 3. 点积的坐标表示法 设 a = a1 ,a2 ,a3 ,b = b1 ,b2 ,b3 则 3 1 1 2 2 3 3 1 i i i a b a b a b a b a b = = + + = 4.几个结论: 由于 1 1 2 2 3 3 a b a b a b a b a b = = + + cos 因此有: 1) 夹角 2 3 2 2 2 1 2 3 2 2 2 1 1 1 2 2 3 3 , arccos ˆ a a a b b b a b a b a b a b + + • + + + + = = 2) a b a b ⊥ =0 ,即 a1b1 + a2b2 + a3b3 = 0

3)aM6a=2b即4=元,i=l,2,3 4) p时i:6)-a-6 际何牙 举例1)已知a={12-1以i={2,1-,求a·6及夹角0 2)给出a,i,c,求(a)e. 三、两个向量的向量积(叉积或外积) 1,两向量的向量积定义: 两向量a与6的向量积是一个新向量c,记为axb=c,且 满足 1bx=郎sn8(9为a,6夹角) 2°a×i1a,axi⊥i,且a,i,a×6构成右手法则。 2.单位向量叉积的性质 ixi=jxj=衣xk=0 ixj=kj×k=i kxi=j jxi=-kk×j=-ii×k=- 3.叉积的运算律 1)axa=0 2)axb=-(bxa) 3)2(axb)=(aad×b 4)ax(B+c)=axb+axc b+cxa=bxa+cxa 4.叉积的坐标表示 设a={a,a2,a},i=6,b2,b}则
3) a b a b // = 即 , 1, 2,3 i i a i b = = 4) prj a ( b )= a b a b ( ) a b prj a b = 举例 1) 已知 a = 1,2,−1,b = − 2,1,−1 ,求 a b 及夹角 2) 给出 a,b,c ,求 (a b c ) . 二、 两个向量的向量积(叉积或外积) 1. 两向量的向量积定义: 两向量 a 与 b 的向量积是一个新向量 c ,记为 a b = c ,且 满足 1 o ab = a b sin ( 为 a,b 夹角) 2 o ab ⊥ a , ab ⊥ b ,且 a,b,ab 构成右手法则。 2. 单位向量叉积的性质 i i = j j = k k = 0 i j = k j k = i k i = j j i = − k k j = −i ik = − j 3. 叉积的运算律: 1) a a = 0 2) ab = −(ba) 3) (ab) = (a)b 4) a b c a b a c + = + ( ) (b + c)a = ba + ca 4. 叉积的坐标表示 设 a = a1 ,a2 ,a3 ,b = b1 ,b2 ,b3 则

。i方 axb=aa a, 66b 5.几个结论 1)a1i台a-i=0,即a,b+a,b+ah=0 2)a1i台axi=0即(a=eg=g=g bb b (这些充要条件在讨论两个向量、两直线、两平面,直 线与平面的平行、垂直、等命题时常用。) axb 3)交角的余弦cos0= 前,交角的正玻为咖 ab 例1)求同时垂直a={12,3},6=(1-3,4的向量 2)给出三角形的3点A,B,C,求其面积S=- 三、混合积*(略) 作业-22页第3题、10题 §8-3曲面及其方程 二·曲面方程的概念 空间曲面S的一般方程为Fx,y,2-0 若(不)在曲面S上的点坐标(不)满足F(x,y,z)0,则F(xy,z小O 称为曲面S的方程,而曲面S称为方程Fk,水20的图象
. 1 2 3 = 1 2 3 = b b b a a a i j k a b 5. 几个结论 1) a b a b ⊥ =0 ,即 a1b1 + a2b2 + a3b3 = 0 2) a // b a b = 0 即 3 3 2 2 1 1 ( ) b a b a b a a = b = = (这些充要条件在讨论两个向量、两直线、两平面,直 线与平面的平行、垂直、等命题时常用。) 3)交角的余弦 cos a b a b = , 交角的正弦为 sin a b a b = 例 1) 求 同时垂直 a = 1,2,3,b = −1,−3,−4 的向量 c 2) 给出三角形的 3 点 A,B,C,求其面积 S =- 三、混合积*(略) 作业-22 页第 3 题、10 题 §8-3 曲面及其方程 一 . 曲面方程的概念 空间曲面 S 的一般方程为 F(x , y , z)=0 若(不)在曲面 S 上的点坐标(不)满足 F(x,y,z)=0,则 F(x,y,z)=0 称为曲面 S 的方程,而曲面 S 称为方程 F(x,y,z)=0 的图象

二,常见的几种曲面方程 1、球面方程:(x-x)+(y-)2+(-)=R2 球心:(6,)半径为R x+y+z-R 球心:(0,0,0)半径为R M1(0,y,z1) 2.旋转曲面方程 平面曲线 旋转轴 旋转曲面方程 ∫f(y,)=0 f±R+y,=0 f,Vx+2)=0 「f(x,y)=0 f飞±2+同=0 =0 f±F+,=0 f(x,)=0 fx,V2+2=0 y=0 f±y+x,=0 例:曲线=式绕乙轴旋转得旋转曲面方程为Z=y+X x=0 例:(P31-一习题10)
二 . 常见的几种曲面方程 1 、球面方程: ( ) ( ) ( ) 2 2 2 2 0 0 0 x x y y z z R − + − + − = 球心: ( x y z 0 0 0 , , ) 半径为 R x 2 + y 2 + z 2 =R 2 球心:(0,0,0) 半径为 R 2. 旋转曲面方程 平面曲线 旋转轴 旋转曲面方程 ( , 0 ) 0 f y z x = = z y ( ) ( ) 2 2 2 2 , 0 , 0 f x y z f y x z + = + = ( , 0 ) 0 f x y z = = x y ( ) ( ) 2 2 2 2 , 0 , 0 f x y z f x z y + = + = ( , 0 ) 0 f x z y = = x z ( ) ( ) 2 2 2 2 , 0 , 0 f x y z f y x z + = + = 例:曲线 2 0 z y x = = 绕 Z 轴旋转得旋转曲面方程为 Z= y 2 + x 2 例:(P 31——习题 10) 1 1 1 M y z (0, , ) z o y d f y z ( , ) 0 =