
第九章多元高数的散分法 §9-1 多元画数的報限及连续 上、多元函数的概念 1.几个概念 1)邻域-一N(x,e)={x小-xke到(开区间 N(P。,E)-{xy)1(x-x。)2+y-y。)2<62}(开圆) NM,s)={Ky1K-xo)2+y-y)2+(E-)》2<82}(开球) 2)区域-一由一条或几条平面曲线围成的部分平面,称为平面 区域;围成平面区域 的曲线称为区域的边界:(不)包含边界的区域称(开)闭区(不) 能用半径为有限值的圆包围的区域称为(无界)有界区域。 (内点,开集,聚点等略) 3)连通区域-一若区域D内任两点,都可用折线联结起来,且该 折线上的点都属于D 的区域。分为单连通区域-一没有洞的 复连通区域-一有洞的 2.多元函数的概念(56页) (二元函数)=fk,y)(Ky)eD (有两个自变量) (三元函数)4=fx,y,) (有三个自变量) (元函数)μ=fx,x2,x3xn) (有n个自变量) 称二元以及二元以上的函数为多元函数二元函数x,y)的图形 是一个曲面(如图)
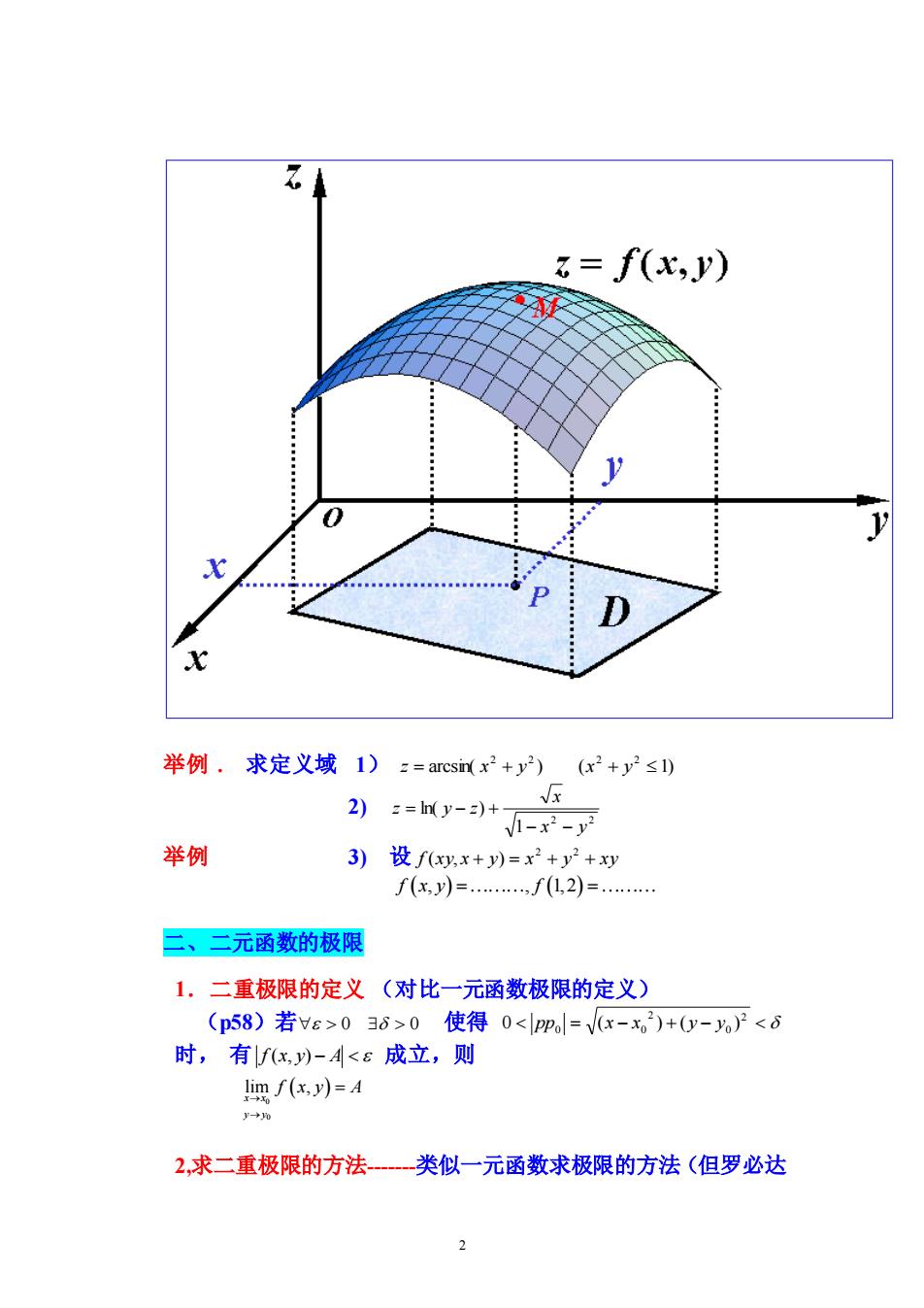
1 第九章 多元函数的微分法 §9-1 多元函数的极限及连续 一、多元函数的概念 1. 几个概念 1)邻域- ( , ) { | | } ( ) N x0 = x x − x0 开区间 N(P , ) {(x, y) | (x - x ) (y - y ) } ( ) 2 2 0 2 0 = 0 + 开圆 N(M , ) {(x, y, z) | (x - x ) (y - y ) ( ) } ( ) 2 2 0 2 0 2 0 = 0 + + z − z 开球 2)区域-由一条或几条平面曲线围成的部分平面,称为平面 区域; 围成平面区域 的曲线称为区域的边界;(不)包含边界的区域称(开)闭区(不) 能用半径为有限值的圆包围的区域称为(无界)有界区域。 (内点,开集,聚点等略) 3)连通区域-若区域 D 内任两点,都可用折线联结起来,且该 折线上的点都属于 D 的区域。分为 −−−−− −−−−− 单连通区域 没有洞的 复连通区域 有洞的 2. 多元函数的概念 (56 页) (二元函数) z=f(x,y) (x,y) D (有两个自变量) (三元函数) = f (x, y,z) (有三个自变量) (n元函数) ( , , ,. ) 1 2 3 n = f x x x x (有n个自变量) 称二元以及二元以上的函数为多元函数 二元函数 z=f(x,y)的图形 是一个曲面(如图)
=f(x,y) 举例.求定义域1)z=aresinx2+y2)(x2+y2≤1) 2)s=n(y-)+ -x2-y 举例 3)设fxyx+y)=x2+y2+xy f(xy)=.,fL,2)= 二、二元函数的极限 1.二重极限的定义(对比一元函数极限的定义) (p58)若∀6>036>0使得0<ppl=V(x-x,2)+y-)2<8 时,有/x,)-<E成立,则 lim f(x.y)=4 → 2,求二重极限的方法一类似一元函数求极限的方法(但罗必达 2
2 举例 . 求定义域 1) arcsin( ) ( 1) 2 2 2 2 z = x + y x + y 2) 2 2 1 ln( ) x y x z y z − − = − + 举例 3) 设 f xy x + y = x + y + xy 2 2 ( , ) f x y f ( , , 1,2 ) = = ( ) 二、二元函数的极限 1.二重极限的定义 (对比一元函数极限的定义) (p58)若 0 0 使得 = − + − 2 0 2 0 0 0 pp (x x ) (y y ) 时, 有 f (x, y) − A 成立,则 ( ) 0 0 lim , x x y y f x y A → → = 2,求二重极限的方法-类似一元函数求极限的方法(但罗必达

法则不能用于求二重极限) 举例-1) 2-xy+4 2) cos 3)1im(1+y)F 3.证明- imxy)不存在,往往采用2种方法之一 「方法一设y=kx和y=k,x分别求出mlxy)的值,若其值不同,则lmxy)不存在 方法二设y=kx求mfxy)=pk),证明不存在 举例4)证:m+少不存在 x-y 三。二元函数的连续(对比一元函数连续定义讲) 设f(x,)在(p)内有定义 若会月=W》@=0,则称y在点() 连续。 若fk,y)在D内每一点都连续,则称fx,y)在D内是连续的。 连续的性质一与一元函数连续的性质类同如: 一切多元函数在定义域所对应的区域内都连续。 连续不极限存在 作业-63页第6(4)、7(2) §9-2偏导数 二、偏导数的定义(64页)
3 法则不能用于求二重极限) 举例- 1) xy xy y x 2 4 lim 0 0 − + → → 2) xy x y y x 1 lim ( ) cos 2 2 0 0 + → → 3) ( ) 1 0 2 lim 1 x x y xy → → + 3.证明- limf(x, y)不存在,往往采用2种方法之一 = = = = y kx, limf(x, y) (k), . x y k limf(x, y) limf(x, y) . 1 2 方法二 设 求 证明不存在 方法一 设 和 分别求出 的值,若其值不同,则 不存在 y k x 举例 4) 证: 不存在 x y x y y x − + → → 0 0 lim 三. 二元函数的连续(对比一元函数连续定义讲) 设 f x y ( , )在U p( 0 )内有定义 若 lim ( , ) ( , ) (or lim z 0) , y 0 x 0 0 0 x x 0 0 = = → → → → f x y f x y y y 则称 f(x,y)在点( 0 0 x , y ) 连续。 若 f(x,y)在 D 内每一点都连续,则称 f(x,y)在 D 内是连续的。 连续的性质—与一元函数连续的性质类同.如: 一切多元函数在定义域所对应的区域内都连续。 连续 ⎯⎯⎯ ⎯⎯⎯→ 一定 不一定 极限存在 作业-63 页第 6(4)、7(2) §9-2 偏 导 数 一、 偏导数的定义(64 页)

设f(x,y)在U(®,)内有定义,若极限 一化+A,存在,则称该极限值为:=化)在点 对x的偏导数,记为f.(x,)或 会ln或lw 即w)=巴+A)- 类似地,定义:=fx,y)在点(x,)对y的偏导数为 f6,)=典出+4)-fx 此时,也称:=x,)在(x)点可导,否则称不可导。 同理,定义:=fx,)对x,y的两个偏导函数(简称为偏导数)为 f(x.y)=lim f(x+△x,y)-f(x,y) △x 或记为察、或 =典y+0》或记为等、哥或 △ 偏导函数的定义类似地可以推广到三元函数以上。 例1)讨论了化=F平列=(00)在(0,0)点的可导性。 0.(x,y)=(0,0) 二、偏函数的求法 求一个多元函数对某个自变量的偏导数时,只要把其他的自变 量视为常数,而对所讨论的自变量利用一元函数的求导公式、法则进 行求导便可。即 器-孟川一少视为常数: 年川—视:为常 数。 类似地可以推广到三元函数以上的偏导数求法, 举例:2)x)=2xy+csy+-smx+2y。求00 3)f,m=2r2+0-)aresin+e。求0,)及.财(0,1) (求下列偏导数)
4 设 f x y ( , )在U p( 0 )内有定义 ,若极限 x f x x y f x y x + − → ( , ) ( , ) lim 0 0 0 0 0 存在,则称该极限值为 z = f (x, y) 在点 ( , ) 0 0 x y 对 x 的偏导数,记为 ( , ) 0 0 ' f x x y 或 ( , ) 0 0 | x y x z 或 ( , ) ' 0 | x x y o z 即 x f x x y f x y f x y x x + − = → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 ' 类似地,定义 ( , ) ( , ) 0 0 z = f x y 在点 x y 对 y 的偏导数为 y f x y y f x y f x y y y + − = → ( , ) ( , ) ( , ) lim 0 0 0 0 0 0 0 ' 此时,也称 z = f (x, y) 在 ( x y 0 0 , ) 点可导,否则称不可导。 同理,定义 z = f (x, y) 对 x, y 的两个偏导函数(简称为偏导数)为 x f x x y f x y f x y x x + − = → ( , ) ( , ) ( , ) lim 0 ' 或记为 x z 、 x f 或 ' x z y f x y y f x y f x y y y + − = → ( , ) ( , ) ( , ) lim 0 ' 或记为 y z 、 y f 或 ' y z 偏导函数的定义类似地可以推广到三元函数以上。 例 1) 讨论 ( ) ( ) ( ) ( ) ( ) 2 2 , , 0,0 , 0, , 0,0 xy x y f x y x y x y = + = 在(0,0)点的可导性。 二、偏函数的求法 求一个多元函数对某个自变量的偏导数时,只要把其他的自变 量视为常数,而对所讨论的自变量利用一元函数的求导公式、法则进 行求导便可。即 f (x, y) dx d x z = - y 视为常数; f (x, y) dy d y z = -视 x 为常 数。 类似地可以推广到三元函数以上的偏导数求法。 举例:2) f x y x y e y x y x ( , ) 2 cos sin 2 2 = + + + 。求 0, 0, 2 2 x y f f 及 3) y e y x f (x, y) = 2x + ( y −1) arcsin + 2 。求 f f x y (0,1 0,1 )及 ( ) (求下列偏导数)
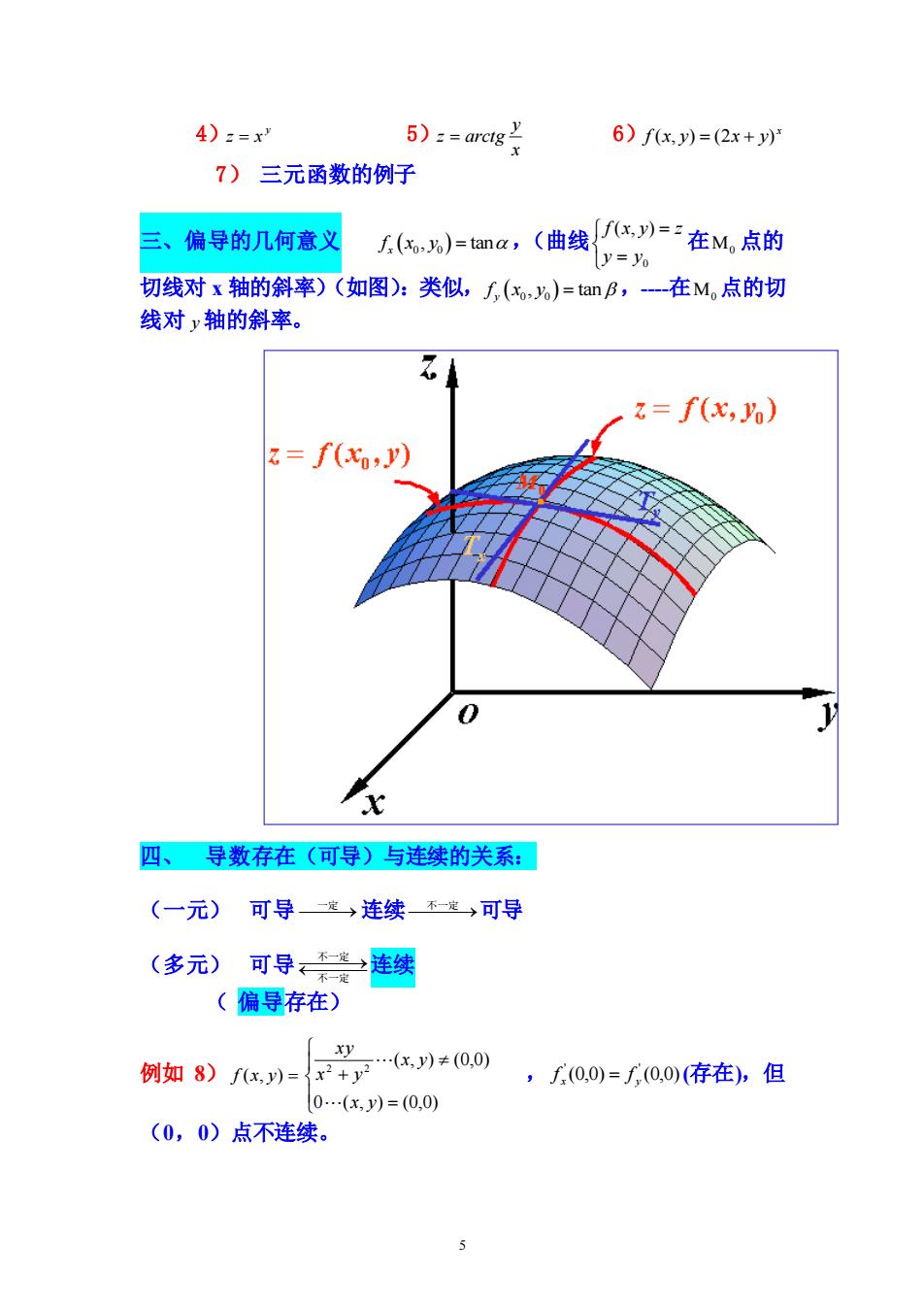
4)z=x 5)==arctg 6)fx,y)=(2x+y) 7)三元函数的例子 三、偏导的几何意义 Ek为)=ama,(曲线/)=F在M,点的 y=% 切线对x轴的斜率)(如图):类似,f(,)=anB,-在M,点的切 线对y轴的斜率。 z=f(x,yo) 3=f(x,) 0 四、导数存在(可导)与连续的关系:】 (一元)可导龙连续一可导 (多元)可导之连绣 (偏导存在) xy 例如8)任m=+少任川*00) ,f(0,0)=∫(0,0(存在),但 0.(x,y)=(0,0) (0,0)点不连续
5 4) y z = x 5) x y z = arctg 6) x f (x, y) = (2x + y) 7) 三元函数的例子 三、偏导的几何意义 f x y x ( 0 0 , tan ) = ,(曲线 = = 0 ( , ) y y f x y z 在 0 点的 切线对 x 轴的斜率)(如图):类似, f x y y ( 0 0 , tan ) = ,-在 0 点的切 线对 y 轴的斜率。 四、 导数存在(可导)与连续的关系: (一元) 可导 ⎯⎯⎯→ 一定 连续 ⎯⎯⎯→ 不一定 可导 (多元) 可导 ⎯⎯⎯ ⎯⎯⎯→ 不一定 不一定 连续 ( 偏导存在) 例如 8) f (x, y) = = + 0 ( , ) (0,0) ( , ) (0,0) 2 2 x y x y x y xy , (0,0) (0,0) ' ' x y f = f (存在),但 (0,0)点不连续

五、高阶偏导数 )腰- )票- 二元二阶偏导数共有4个 )-1列 )器 一般上,f不等于f。但若f与f:连续,则f=f。(求导次序无 关定理) 例:》:=h芳 求二阶偏导数: 10)u=2+y2+证:0++0u-2」 x2+v2+z2 作业:69页-第1(3),(6;7题 §9-3金散分及其寇用 一、全微分的定义(70页) (以一元函数的微分概念引进) 若:=f,)在点(x,y)处的全增量△=fx+△x,y+)-x,)可以表 示为△=A·△r+B·△y+o(p) (其中:A,B与△x,4y无关,p=V△r2+Ay) 则称:=f(x,)在点(x,y)处可微(微分存在),且称A△x+B·Ay为 6
6 五、 高阶偏导数 二元二阶偏导数共有 4 个 ( ) ( ) ( ) ( ) 2 2 2 2 2 2 , , , , xx yy xy yx z z f x y x x x z z f x y y y y z z f x y y x x y z z f x y x y y x = = = = = = = = 一般上, '' xy f 不等于 '' yx f 。但若 '' xy f 与 '' yx f 连续,则 '' xy f = '' yx f 。(求导次序无 关定理) 例:9) y x z 2 = ln 求二阶偏导数; 10) 2 2 2 u = x + y + z 证: z u u y u x u 2 2 2 2 2 2 2 = + + 。 作业:69 页-第 1(3),(6); 7 题 §9-3 全 微 分 及 其 应 用 一、 全微分的定义(70 页) (以一元函数的微分概念引进) 若 z = f (x, y) 在点( x, y )处的全增量 z = f (x + x, y + y) − f (x, y) 可以表 示为 z = A .x + B y +() (其中:A, B 与 x,y 无关, 2 2 = x + y ) 则称 z = f (x, y) 在点( x, y )处可微(微分存在),且称 Ax + B y 为

y=∫x,y)在点(x,y)的全微分,记为d或(x,)即 k=A△x+B·Ay 或df(x,y)=A△r+B.Ay 二、可微的必要条件: 若:=x,)在点(x,y)可微,则在点(x,)的两个偏导存在。且 4=症B=房,此时,y=x0在点x圳的微分记为: (三元函数的全微分) (举例) 1Df现-ea求列 2):=amcg上求止(两种方法求) 3)(三元)M=e片求d 三、可微、可导、连续的关系 (多元函数) 可微是可导不是号连续 一 存在连续的人不可微不连续 四、全微分在近似计算中的应用 当|△xb△y1很小时,△≈止所以有 f(x0+△x,%+△y≈f(xo,o)+f(x0,o)△x+f,(xo,6)Ay 例:求2.96)2+(4.05)的近似值。(设fx,)=√x2+y,x。=3,%=4求) 作业:76页-1(2),(4):2
7 y = f (x, y) 在点 (x, y) 的全微分,记为 dz或df (x, y) 即 dz = Ax + B y 或 df (x, y) = Ax + B y 二、 可微的必要条件: 若 z = f (x, y) 在点 (x, y) 可微,则在点 (x, y) 的两个偏导存在。且 y z B x z A = = , ,此时 , y = f (x, y) 在点 (x, y) 的微分记为: z z dz dx dy x y = + 或 df x y f x y dx f x y dy x y ( , ) ( , ) ( , ) ' ' = + (三元函数的全微分) dz z u dy y u dx x u u f x y z du + + = ( , , ), = (举例) 1) ( ) ( ) 2 2 2 , , , x y t y f x y e dt df x y + = 求 2) x y z = arctg 求 dz (两种方法求) 3)(三元) x y z u e + = 求 du 三、 可微、可导、连续的关系 (多元函数) 可微 ⎯⎯⎯ ⎯⎯⎯→ 一定 不一定 可导 ⎯⎯⎯ ⎯⎯⎯→ 不一定 不一定 连续 存在连续的 , x y f f ⎯⎯⎯ ⎯⎯⎯→ 一定 不一定 可微 ⎯⎯⎯ ⎯⎯⎯→ 一定 不一定 连续 四、 全微分在近似计算中的应用* 当| x |,| y |很小时,z dz, 所以有 f x x y y f x y f x y x f x y y ( + , + ) ( , ) + x ( , ) + y ( 0 , 0 ) ' 0 0 ' 0 0 0 0 例:求 2 2 (2.96) + (4.05) 的近似值。(设 f (x, y) = x 2 + y 2 , x0 = 3, y0 = 4求 ) 作业:76 页-1(2),(4); 2

§9-4多元复合函数的求导法则 二、两个中间变量的情形(条件见1页定理2.) ==f(u,v),u=u(x,y),v=v(x,y) dz dz du dz dv d证a证dl,zv ax ou dx ov dx 求导思路图:(画图) 】》您=+)列存在连续的=价份号致,求会等及票: 二、三个中间变量的情形(78页(5)(6)式) 2=f(u.y.e) u=u(x.v),v=v(x.v),w=w(x.v) 正-u+m+正r 正_正+正a+正aw dx ou dx ov ox ow dx 西+am0 求导思路图:(画图) 三、只有一个中间变量的情形(9页) z=f(u,x,) =x,y) +兴 dydy ou dy 求导思路图: (画图)
8 §9-4 多元复合函数的求导法则 一、 两个中间变量的情形(条件见 77 页定理 2 ) z = f (u,v),u = u(x, y), v = v(x, y) x v v z x u u z x z + = , y v v z y u u z y z + = 求导思路图: (画图) 举例 1) 2 , cos , , xy z z z uv u x y v e x y = = = 求 及 。 2) ( ) 2 2 2 , , z z z z f x y x y x y x = + 设 存在连续的二阶偏导数,求 及 。 二、 三个中间变量的情形(78 页-(5)(6)式) z = f (u,v,w) ,u = u(x, y) , v = v(x, y) , w = w(x, y) x w w z x v v z x u u z x z + + = y w w z y v v z y u u z y z + + = 求导思路图:(画图) 三、 只有一个中间变量的情形(79 页) z = f (u, x, y) u = u(x, y) x u u f x f x z + = y u u f y f y z + = 求导思路图: (画图)

设:=y+xF(u),u=上,F(u)可导,证明: 举例3) 会+房-*w 四、只有一个自变量的情形(77页一(1)式) 2=f(u,),u=(x),v=v(x) (全导数) 求导思路图:(画图) 举例):=e心,==m求会 四、全微分形式的不变性:(81页) 止加+ 不论、y是“中变”或“自变”均成立。 求“复函”的导数时要注意的原则: 1弄清复合关系。分清“中变”与“自变”。 2对某个自变量求偏导时,应注意一切的“中变”而归结到 该自变量。 3求高阶偏导时,应注意对一阶偏导数来说是保持原来的复合关系 举例5)=xy,求止(两种方法求) 作业:(8283页6:8(1):10) §9-5德离数及其散分法
9 举例 3) ( ), , ( ) y z xy xF u u F u x z z x y z xy x y = + = + = + 设 可导,证明: 四 、只有一个自变量的情形(77 页-(1)式) z f u v = ( , ),u = u(x) , v = v(x) dx dv v z dx du u z dx dz . . + = (全导数) 求导思路图:(画图) 举例 4) 2 2 , , sin , u v dz z e u x v x dx − = = = 求 。 四、 全微分形式的不变性:(81 页) - dv v z du u z dz + = 不论 u、v 是“中变”或“自变”均成立。 求“复函”的导数时要注意的原则: 举例 5) , y x z x y dz = 求 (两种方法求) 作业:(82—83 页 6; 8(1);10) §9-5 隐 函 数 及 其 微 分 法 3. . 2. 1. 求高阶偏导时,应注意对一阶偏导数来说是保持原来的复合关系 该自变量。 对某个自变量求偏导时,应注意一切的“中变”而归结到 弄清复合关系。分清“中变”与“自变

二、一个方程所确定的隐函数 1、一元隐函数F(x,y)=0的求导公式: (满足条件:F,F,F存在且连续,F≠0) (证明一下) 举例:1D=2-e求密 2)设LnF+于=arctan上求虫。 dx 2、二元隐函数F(x,y,)=0的求导公式 (满足条件:F,F,F存在且连续,F≠0) 周 会张周 (证明) 例:3)设x+y=3xy+Ln上(用徽分法与公式法求) 求正 dx'dy 4)设r2++2=2,求及图 a'ar2。 5)设F5=0,求 二、方程组所确定的隐函数 设方程组怎y弘)=0确定函数u=Mx,Y=x,),且 G(x,4,v)=0 密密容均存在。则当雅可比(uaw)行列式 -9660 有:尝近 注意:一个方程的隐函数用公式法求导;但方程组的隐函数则用-
10 一、 一个方程所确定的隐函数 1、一元隐函数 F(x, y) = 0 的求导公式: (满足条件: ' ' ' , , Fx Fy Fz 存在且连续, 0 ' Fy ) ( , ) ( , ) ' ' F x y F x y dx dy y x = − (证明一下) 举例:1) 0 2 | = − x= y dx dy y xe 求 。 2) 2 2 arctan y Ln x y x 设 + = 求 dx dy 。 2、二元隐函数 F(x, y,z) = 0 的求导公式 (满足条件: ' ' ' , , Fx Fy Fz 存在且连续, 0 ' F z ) ( ) ( ) , , , , x z z F x y z x F x y z = − ( ) ( ) , , , , y z z F x y z x F x y z = − (证明) 例:3) 设 z y x + y = 3xy + Ln (用微分法与公式法求 ) 求 y z x z , 。 4) 2 2 2 2 2 2 , , z z z x y z z x y x + + = 设 求 及 。 5) 设 ( , ) = 0 z y z x F ,求 y z x z , 。 二、方程组所确定的隐函数 设方程组 ( ) ( ) , , , 0 , , , 0 F x y u v G x y u v = = 确定函数 u = u(x, y) ,v = v(x, y),且 y v x v y u x u , , , 均存在。则当雅可比( Jacobi )行列式 | | 0 ( , ) ( , ) = = x v u v G G F F u v F G J 有: | | 1 x v x v G G F F x J u = − | | 1 y v y v G G F F y J u = − | | 1 u x u x G G F F x J v = − | | 1 u y u y G G F F y J v = − 注意:一个方程的隐函数用公式法求导;但方程组的隐函数则用-