
《离散数学》教学大纲 (Discrete Mathematics) 适用专业:电子信息类 课程类别:学科基础课 课程学时:48 课程学分:3.0 先修课程:高等数学、线性代数等 一、课程简介 离散数学是研究离散量的结构及其相互关系的数学学科,是现代数学的一个重要分支,是 计算机科学中基础理论的核心课程,是计算机科学与技术的支撑学科。它在计算机科学与枝术 领域有者广泛的应用,同时离散数学也是计算机专业的许多专业课程,如程序设计语言、数据 结构、操作系统、编译技术、人工智能与机器人、数据库、网络、计算机图形学、算法设计与 分析、理论计算机科学基础等必不可少的先行课程。通过离散数学的 习,不但可以掌握离 结构的描述工具和处理方法,为后续课程的学习创造条件,而且可以提高抽象思维和严格的迈 粗推理能力,为将来参与创新性的研究和开发工作打下坚实的基础。 二、教学目的与任务 离散数学是一门培养学生缜密思维、严格推理,具有综合归纳分析能力的课程。通过本课 程的学习,使学生有一定的严格逻辑推理与抽象思维能力,掌据离散量的处理及运算技能,能 够将离散数学应用到解决计算机技术中的实际题中。 仅能为学生莫 定计算机科学的专业基 础,并且能为将后续课程的学习及将来开发软、硬件技术及研究、应用提供有力的工具。 三、课程内容 第1章命题逻辑的基本概念 11命题与联结词 1.2命题公式及其赋值 第2章命题逻辑等值演 2.1等值式 2.2析取范式与合取范式 ◆2.3联结词的完备集 *2.4可满足性问题与消解法 第3章命愿逻辑的推理理论 3.1推理的形式结构 3.2自然推理系统P
《离散数学》教学大纲 (Discrete Mathematics) 适用专业:电子信息类 课程类别:学科基础课 课程学时:48 课程学分:3.0 先修课程:高等数学、线性代数等 一、课程简介 离散数学是研究离散量的结构及其相互关系的数学学科,是现代数学的一个重要分支,是 计算机科学中基础理论的核心课程,是计算机科学与技术的支撑学科。它在计算机科学与技术 领域有着广泛的应用,同时离散数学也是计算机专业的许多专业课程,如程序设计语言、数据 结构、操作系统、编译技术、人工智能与机器人、数据库、网络、计算机图形学、算法设计与 分析、理论计算机科学基础等必不可少的先行课程。通过离散数学的学习,不但可以掌握离散 结构的描述工具和处理方法,为后续课程的学习创造条件,而且可以提高抽象思维和严格的逻 辑推理能力,为将来参与创新性的研究和开发工作打下坚实的基础。 二、教学目的与任务 离散数学是一门培养学生缜密思维、严格推理,具有综合归纳分析能力的课程。通过本课 程的学习,使学生有一定的严格逻辑推理与抽象思维能力,掌握离散量的处理及运算技能,能 够将离散数学应用到解决计算机技术中的实际问题中。不仅能为学生奠定计算机科学的专业基 础,并且能为将后续课程的学习及将来开发软、硬件技术及研究、应用提供有力的工具。 三、课程内容 第 1 章 命题逻辑的基本概念 1.1 命题与联结词 1.2 命题公式及其赋值 第 2 章 命题逻辑等值演算 2.1 等值式 2.2 析取范式与合取范式 * 2.3 联结词的完备集 * 2.4 可满足性问题与消解法 第 3 章 命题逻辑的推理理论 3.1 推理的形式结构 3.2 自然推理系统 P

3.3消解证明法 第4章 一阶逻辑基本概念 阶逻辑命题符号化 4.2一阶逻辑公式及其解 第5章一阶逻辑等值演算与推理 51一阶逻辑等值式与置换规则 52一阶逻辑前束范式 价逻辑的推理理论 第6章集合代数 6.1集合的基本概念 6.2集合的运算 63有穷集的计数 64集合恒等式 第7 7.1有序对与笛卡儿积 72二元关系 7.3关系的运算 7.4关系的性质 75关系的闭包 7.6等价关系与划分 7.7偏序关系 第8章函数 81函数的定义与性质 8.2函数的复合与反函数 ·83双射函数与集合的基数 *8.4一个电话系统的描述实例 第14章图的基本概念 141图 142通路与同改 14.3图的连通性 14.4图的矩阵表示 *14.5图的运算 第15章欧拉图与哈密顿图 15.1欧拉图 15.2哈密顿图 15.3最短路问题、中国邮递员问题与货郎担问题 第16章树 16.1无向树及其性质 16.2生成树 16.3根树及其应用
3.3 消解证明法 第 4 章 一阶逻辑基本概念 4.1 一阶逻辑命题符号化 4.2 一阶逻辑公式及其解释 第 5 章 一阶逻辑等值演算与推理 5.1 一阶逻辑等值式与置换规则 5.2 一阶逻辑前束范式 * 5.3 一阶逻辑的推理理论 第 6 章 集合代数 6.1 集合的基本概念 6.2 集合的运算 6.3 有穷集的计数 6.4 集合恒等式 第 7 章 二元关系 7.1 有序对与笛卡儿积 7.2 二元关系 7.3 关系的运算 7.4 关系的性质 7.5 关系的闭包 7.6 等价关系与划分 7.7 偏序关系 第 8 章 函数 8.1 函数的定义与性质 8.2 函数的复合与反函数 * 8.3 双射函数与集合的基数 * 8.4 一个电话系统的描述实例 第 14 章 图的基本概念 14.1 图 14.2 通路与回路 14.3 图的连通性 14.4 图的矩阵表示 * 14.5 图的运算 第 15 章 欧拉图与哈密顿图 15.1 欧拉图 15.2 哈密顿图 15.3 最短路问题、中国邮递员问题与货郎担问题 第 16 章 树 16.1 无向树及其性质 16.2 生成树 16.3 根树及其应用
三、课程学时分配、教学内容与教学基本要求 周序 章节 教学内容 学时 第1周 第1章命题逻辑基本概念 命题与复合命题、命题公式与真值表、蕴含 、赋值 3 第2周 第2章命颗罗辑等值演算 等值式、析取范式与合取范式、完备集、可满 足性 第3周 第3章命题逻辑推理理论 推理形式结构、推理定律、推理系统、消解证 3 第4周 第4章一阶逻辑基本概念 谓词与量词、命题符号化、谓词公式、赋值与 解释 3 第5章一阶逻辑等值演算马 第5周 等值式与置换规侧、前束范式、推理理论 推理 第6周 第6章集合论 集合、集合运算、集合计数 3 第7周 第6章集合论 集合恒等式、集合练习 3 第8周 第7章二元关系 有序对、笛卡尔积、二元关系、关系的运算 第9周 第7章二元关系 关系的性质、关系的闭包 第10周第7章二元关系 等价关系与别分、偏序关系 第1周第8章函数 定义与性质、函数复合、反函数 3 第12周 第8章函数 双射函数 基数 第14章图的基本概念 图的概念及连通性、 3 第13周第14章图的基本概念 图的矩阵表示、图的运算 第14周第15章欧拉图与哈密顿图 欧拉图与哈密顷图 3 第15周 第16章树 无向树、生成树、根树 第16周总复习 四、教学方法与教学手段说明 该课程教学方式主要有:课堂教学、交互学习、课后作业。理论课采用多媒体和传统黑板 式教学相结合的教学手段,制作了涵盖课程基本和主要教学内容的多媒体课件、准备了相关的 辅助教学资料。交互学习包括课堂上的提问、讨论、作业和抽查等,目的是培养学生的自主学 习意识和自学能力,促进个性化的能力发展。课程综合练习以提高学生的应用能力。鼓励学生 多做相关练习
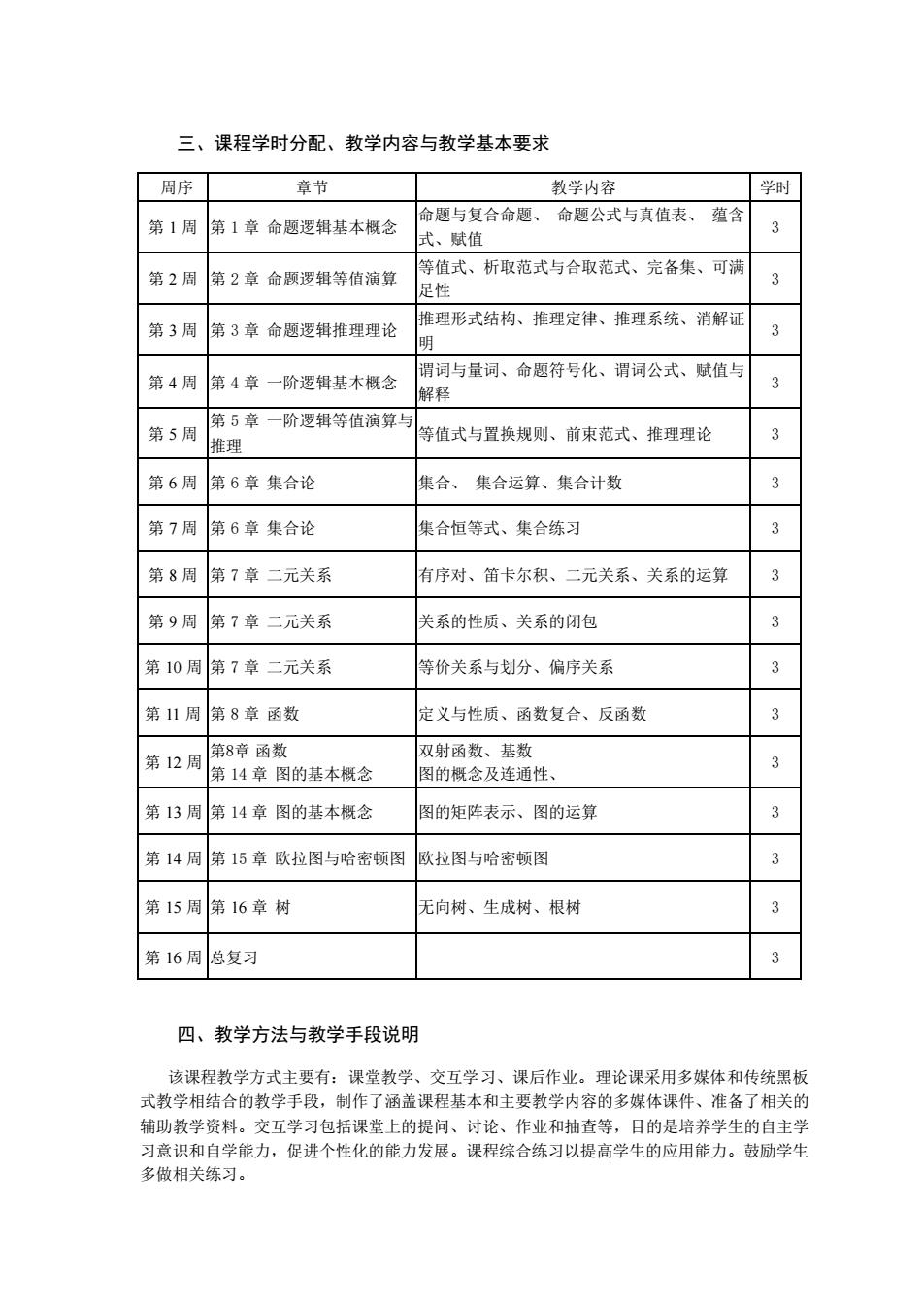
三、课程学时分配、教学内容与教学基本要求 周序 章节 教学内容 学时 第 1 周 第 1 章 命题逻辑基本概念 命题与复合命题、 命题公式与真值表、 蕴含 式、赋值 3 第 2 周 第 2 章 命题逻辑等值演算 等值式、析取范式与合取范式、完备集、可满 足性 3 第 3 周 第 3 章 命题逻辑推理理论 推理形式结构、推理定律、推理系统、消解证 明 3 第 4 周 第 4 章 一阶逻辑基本概念 谓词与量词、命题符号化、谓词公式、赋值与 解释 3 第 5 周 第 5 章 一阶逻辑等值演算与 推理 等值式与置换规则、前束范式、推理理论 3 第 6 周 第 6 章 集合论 集合、 集合运算、集合计数 3 第 7 周 第 6 章 集合论 集合恒等式、集合练习 3 第 8 周 第 7 章 二元关系 有序对、笛卡尔积、二元关系、关系的运算 3 第 9 周 第 7 章 二元关系 关系的性质、关系的闭包 3 第 10 周 第 7 章 二元关系 等价关系与划分、偏序关系 3 第 11 周 第 8 章 函数 定义与性质、函数复合、反函数 3 第 12 周 第8章 函数 第 14 章 图的基本概念 双射函数、基数 图的概念及连通性、 3 第 13 周 第 14 章 图的基本概念 图的矩阵表示、图的运算 3 第 14 周 第 15 章 欧拉图与哈密顿图 欧拉图与哈密顿图 3 第 15 周 第 16 章 树 无向树、生成树、根树 3 第 16 周 总复习 3 四、教学方法与教学手段说明 该课程教学方式主要有:课堂教学、交互学习、课后作业。理论课采用多媒体和传统黑板 式教学相结合的教学手段,制作了涵盖课程基本和主要教学内容的多媒体课件、准备了相关的 辅助教学资料。交互学习包括课堂上的提问、讨论、作业和抽查等,目的是培养学生的自主学 习意识和自学能力,促进个性化的能力发展。课程综合练习以提高学生的应用能力。鼓励学生 多做相关练习

五、考核方式和要求 本课程考核由期末卷面考试、平时考勤、平时作业等部分组成。其中,期末卷面考试采用 教考分离闭卷方式。 总评成绩的构成: 令期末考试:70%: 令平时成绩含平时考勤、提问、作业:30% 六、教材及主要参考书目 主讲教材: 《离散数学》,屈婉玲、耿素云、张立昂编著,高等教育出版社 参考书目: 《离散数学学习指导与习题解析》,屈婉玲、耿素云、张立昂编著,高等教育出版社 2.《离散数学导论》(第二版),徐洁磐编著,高等教有出版社 3.《离散数学》,左孝凌、李为槛、刘水才编著,上海科学技术文献出版社 4.《离散数学》,歌素云、屈婉玲、张立品编著,清华大学出版社 5.《离散数学结构》(影印版英文),Ko 编著,高等教有出版社 6.《离散数学》钟声、张晋、云敏、冯思玲, 参考网站: 屈婉玲北京大学2005年国家级精品课程 http://www.jingpinke.com/xpe/portal/270863e5-1189-1000-8dc9-ac9dee6259387uuid=8a833996 -18ac928d-0118-ac928f68-024a&courselD=A050083 ·上海交通大学离散数学视频 http://v.youku.com/v show/id XN ig3MTcINig=.html?f=2932350 执笔人:李怀成、台安 审核人:常领、唐朝胜 更新日期:2018年3月
五、考核方式和要求 本课程考核由期末卷面考试、平时考勤、平时作业等部分组成。其中,期末卷面考试采用 教考分离闭卷方式。 总评成绩的构成: 期末考试:70%; 平时成绩含平时考勤、提问、作业:30%。 六、教材及主要参考书目 主讲教材: 《离散数学》,屈婉玲、耿素云、张立昂 编著,高等教育出版社 参考书目: 1.《离散数学学习指导与习题解析》,屈婉玲、耿素云、张立昂 编著,高等教育出版社 2.《离散数学导论》(第二版),徐洁磐 编著,高等教育出版社 3.《离散数学》,左孝凌、李为槛、刘永才 编著,上海科学技术文献出版社 4.《离散数学》,耿素云、屈婉玲、张立昂 编著,清华大学出版社 5.《离散数学结构》(影印版英文),Kolman 编著,高等教育出版社 6.《离散数学》钟声、张晋、云敏、冯思玲,中国铁道出版社 参考网站: ⚫ 屈婉玲北京大学 2005 年国家级精品课程 http://www.jingpinke.com/xpe/portal/270863e5-1189-1000-8dc9-ac9dee625938?uuid=8a833996 -18ac928d-0118-ac928f68-024a&courseID=A050083 ⚫ 上海交通大学离散数学视频 http://v.youku.com/v_show/id_XNjg3MTc1Njg=.html?f=2932350 执笔人:李怀成、台安 审核人:常颖、唐朝胜 更新日期:2018 年 3 月