
第六章定积分的应用 §6-1定积分的元素法 (Element method of definite integral) 利用定积分解决问题时,往往要经过如下几个步 骤: 细分(分割)、近似代替(粗)、求和(合)、取 极限(精)即: 1,细分[a,b小,确定线段元素kx+上局部量AF 的近似值fx)d,称为总量F的元素,记作: AF=f(x)dx 2,以F的元素fx为积分表达式,在a,b上积 分,便得到总量F的表达式: F=[f(x)dx 这种用量F的微分元素fx)进行积分而得到量F 的方法称为定积分的元素法(微元法)
1 第六章 定积分的应用 §6-1 定积分的元素法 (Element method of definite integral) 利用定积分解决问题时,往往要经 过如下几个步 骤: -细分 (分 割)、 近似 代替( 粗)、求和 (合)、取 极限(精)即: 1, 细分 a,b ,确定线段元素 x, x + dx 上局部量 F 的近似值 f (x)dx ,称为总量 F 的元素,记作: F = f (x)dx 2, 以 F 的元素 f (x)dx 为积分表达式,在 a,b 上积 分,便得到总量 F 的表达式: = b a F f (x)dx 这种用量 F 的微分元素 f (x)dx 进行积分而得到量 F 的方法称为定积分的元素法(微元法)
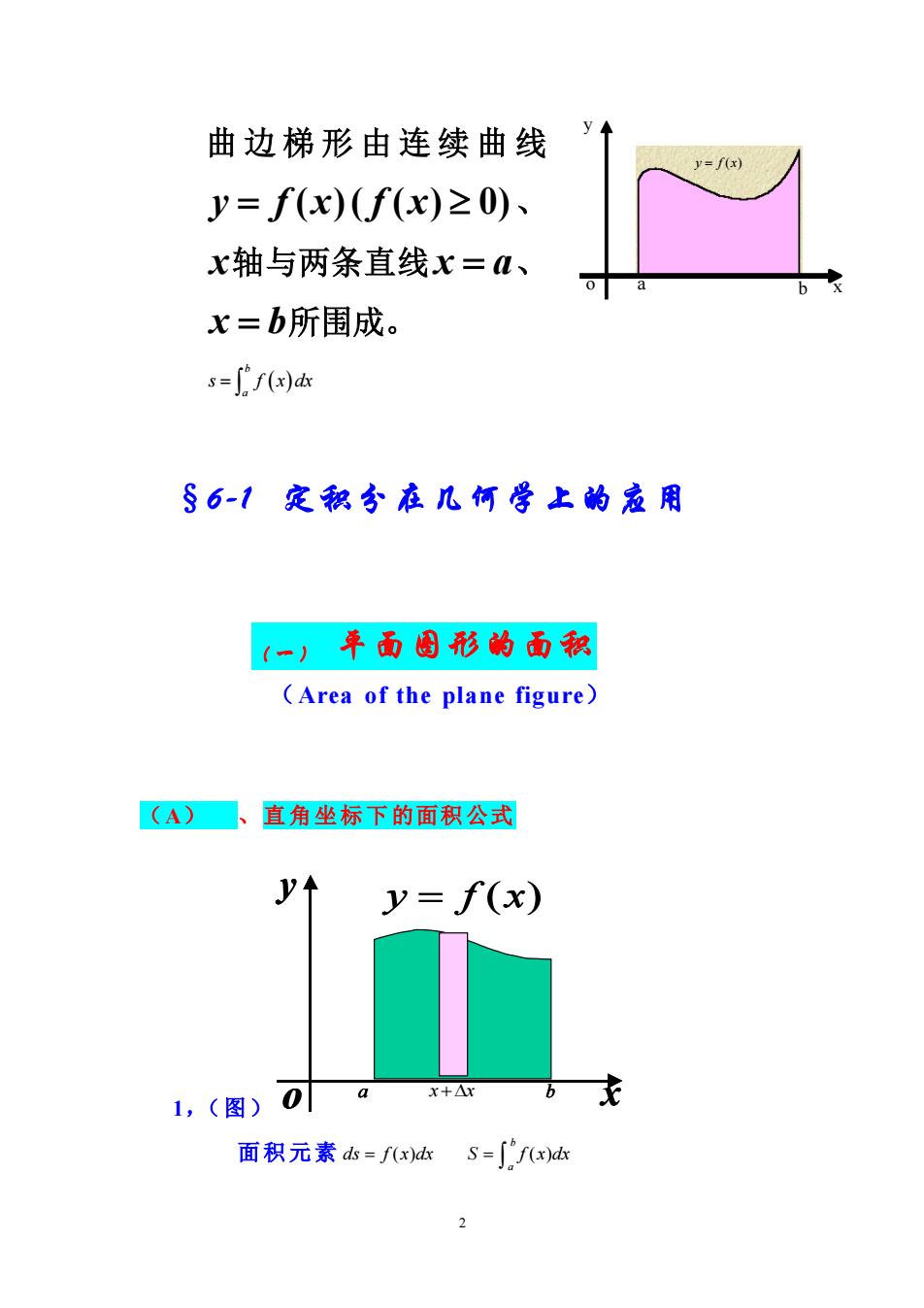
曲边梯形由连续曲线 =f(x y=f(x)(f(x)≥0)、 x轴与两条直线x=M、 x=b所围成。 s=["f(x)dx §6-1定积分在几何学上的爱用 一)年面因形的西积 (Area of the plane figure) (A)■、直角坐标下的面积公式 Jy↑ y=f(x) 1,(图)0a x+Ar 面积元素d=f(x)dkS=∫f(x)d达 2
2 ( ) b a s f x dx = §6-1 定积分在几何学上的应用 (一) 平面图形的面积 (Area of the plane figure) (A) 、直角坐标下的面积公式 1,(图) 面积元素 = = b a ds f (x)dx S f (x)dx 曲边梯形由连续曲线 y = f (x)( f (x) 0)、 x轴与两条直线 x = a、 x = b所围成。 a b x y o y f x = ( ) x y o y f x = ( ) a b x y o y f x = ( ) a b x y o y f x = ( ) a x x + b
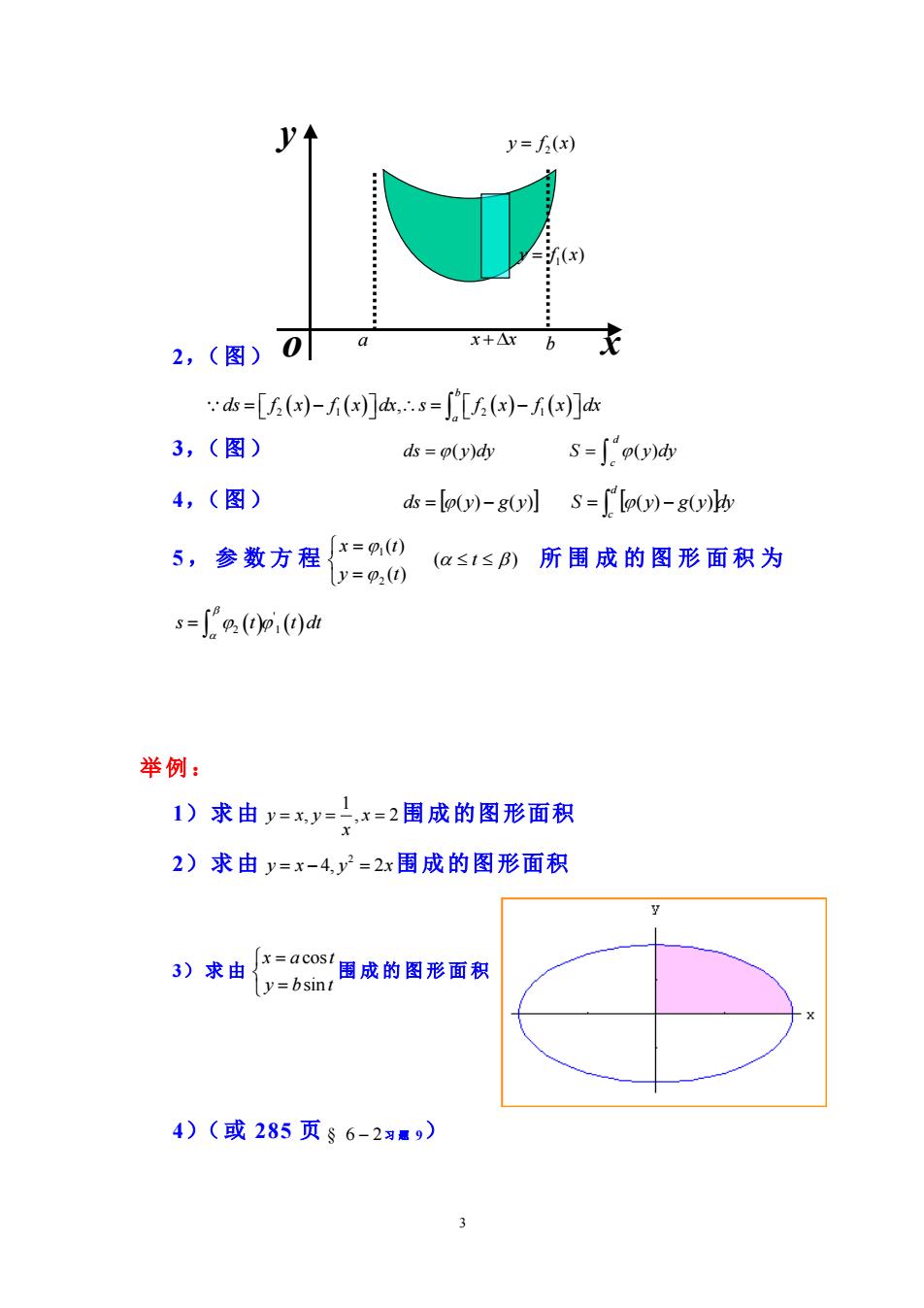
y=f(x) 2,(图)0a d=[5(x)-f(x]s=∫[5(x-f(x)] 3,(图) ds=p(y)dy S=∫py)d 4,(图) ds =[o(y)-g(y)]s=[[o(y)-g(y) 5,参数方程=0 y=p2(0) (a≤1≤B)所围成的图形面积为 s=∫%,p0dh 举例: 1)求由y==2围成的图形面积 2)求由y=x-4,y2=2x围成的图形面积 3)求由=co1围成的图形面积 y=bsint 4)(或285页§6-2习题9)
3 2,(图) 2 1 2 1 ( ) ( ) , ( ) ( ) b a ds f x f x dx s f x f x dx = − = − 3,(图) = = d c ds ( y)dy S ( y)dy 4,(图) ds y g y S y g y dy d c = ( ) − ( ) = ( ) − ( ) 5 , 参 数 方 程 ( ) ( ) ( ) 2 1 = = t y t x t 所 围 成 的 图 形 面 积 为 ( ) ( ) ' 2 1 s t t dt = 举例: 1)求由 1 y x y x , , 2 x = = = 围成的图形面积 2)求由 2 y x y x = − = 4, 2 围成的图形面积 3)求由 cos sin x a t y b t = = 围成的图形面积 4)(或 285 页 § 6 − 2 习 题 9) x y o 1 y f x = ( ) 2 y f x = ( ) a x x + b
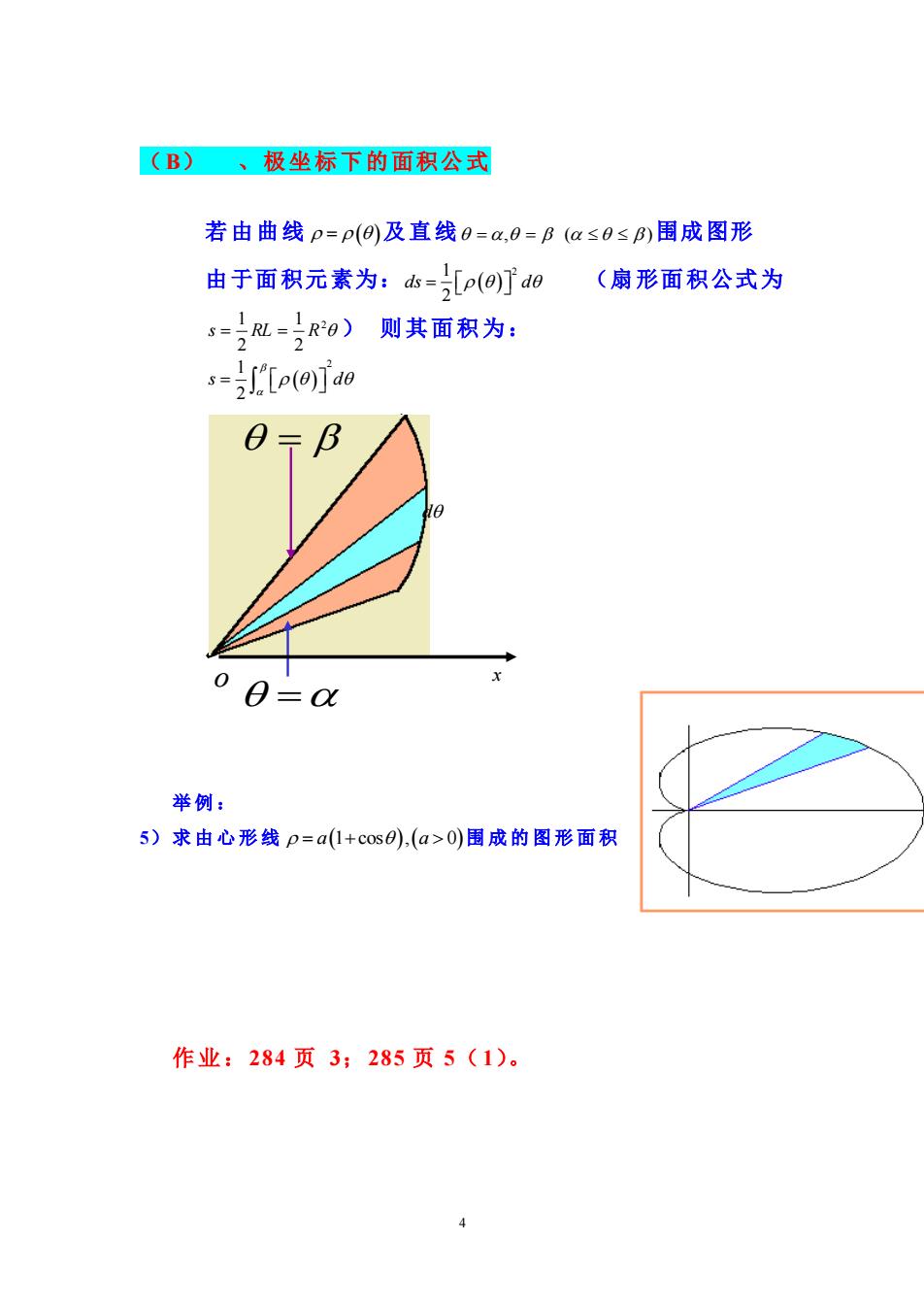
(B)、极坐标下的面积公式 若由曲线p=p(⊙)及直线a=a,B=B(as0sB)围成图形 由于面积元素为:山=[p(]d0(扇形面积公式为 s=L=)R阳)则其面积为: s=Le(0)Jdo 0=B 0=0 举例: 5)求由心形线p=a1+cos0),(a>0)围成的图形面积 作业:284页3;285页5(1)
4 (B) 、极坐标下的面积公式 若由曲线 = ( ) 及直线 =, = ( ) 围成图形 由于面积元素为: ( ) 1 2 2 ds d = (扇形面积公式为 2 2 1 2 1 s = RL = R ) 则其面积为: ( ) 2 1 2 s d = 举 例 : 5)求由心形线 = + a a (1 cos , 0 ) ( ) 围成的图形面积 作业:284 页 3;285 页 5(1)。 = d = = o x

二、儿何体的体积 Volume of the geometries solid) (A)、旋转体的体积 1,由连续曲线y=fx)以及直线x=a,x=b(a<b),y=0围成 的图形绕着0x轴旋转所得的几何体的体积为:(画图) y=πf(x) (分析:体积元素 h=πf2(x))) (Y,=2πxf(x)k,(P286-19题) 2,类似(如图)y=π20y),(=2πo(y)) 3,同理(如图) V,=πr2(x)-g2(x (V,=2πx[fx)-g(x)]) 举例: 1),求由y=sinx,(0≤x≤),y=1,x=0围成的图形分别绕着 0x、oy轴旋转所得的几何体的体积V,V,(图)。 2),+少=R绕ax旋转所得的球体r=号R。 3),曲线=1十及其渐近线围成的图形绕其渐近线旋转 1 所得的旋转体的体积V=. 4)举例(P280例8) 5
5 ( 二 )、 几何体的体积 (Volume of the geometries solid) (A)、旋转体的体积 1, 由连续曲线 y = f (x) 以及直线 x=a,x=b (a<b),y=0 围成 的图形绕着 ox 轴旋转所得的几何体的体积为:(画图) V f x dx b a x ( ) 2 = ( 分 析 : 体 积 元 素 ( ( ) ) 2 dv = f x dx ) ( ( ) ) 2 , 286 19 b y a V xf x dx P = − − ( 题) 2, 类似(如图) = d c Vy (y)dx 2 , ( 2 ( ) d x c V y y dy = ) 3,同理(如图) = − b a Vx f (x) g (x) dx 2 2 ( 2 ( ) ( ) b y a V x f x g x dx = − ) 举例: 1),求由 sin ,(0 ), 1, 0 2 y x x y x = = = 围成的图形分别绕着 ox、 oy 轴旋转所得的几何体的体积 Vx , Vy (图)。 2), 2 2 2 3 3 4 x + y = R 绕ox旋转所得的球体V = R 。 3), 2 1 1 y x = + 曲线 及其渐近线围成的图形绕其渐近线旋转 所得的旋转体的体积V= 4)举例(P280 例 8)

作业:285页12:286页15(3). (B)、截面面积已知的几何体体积 若垂直于某坐标轴(x)的各截面的面积已知A(x),(a≤x≤b), 则其体积为: V=∫Ax)d (=4x)k)(画图) 举例5)(P281例10) (或286页习题14) 红、年面曲线的欧长 Length of the plane curve) (A)、直角坐标下的弧长公式 1、普通方程情形: 设曲线y=-f(x)为光滑曲线(或分段光滑曲线)(即存在连 续的导数)
6 作业:285 页 12;286 页 15(3)。 (B)、 截面面积已知的几何体体积 若垂直于某坐标轴(x)的各截面的面积已知 A(x),( a x b ), 则其体积为: = b a V A(x)dx (∵ dv = A(x)dx )(画图) 举例 5) (P281 例 10) (或 286 页习题 14) ( 三 )、 平面曲线的弧长 (Length of the plane curve) (A) 、直角坐标下的弧长公式 1、 普通方程情形: 设曲线 y = f (x) 为光滑 曲 线 ( 或 分 段 光 滑 曲线)( 即 存 在 连 续的导数)
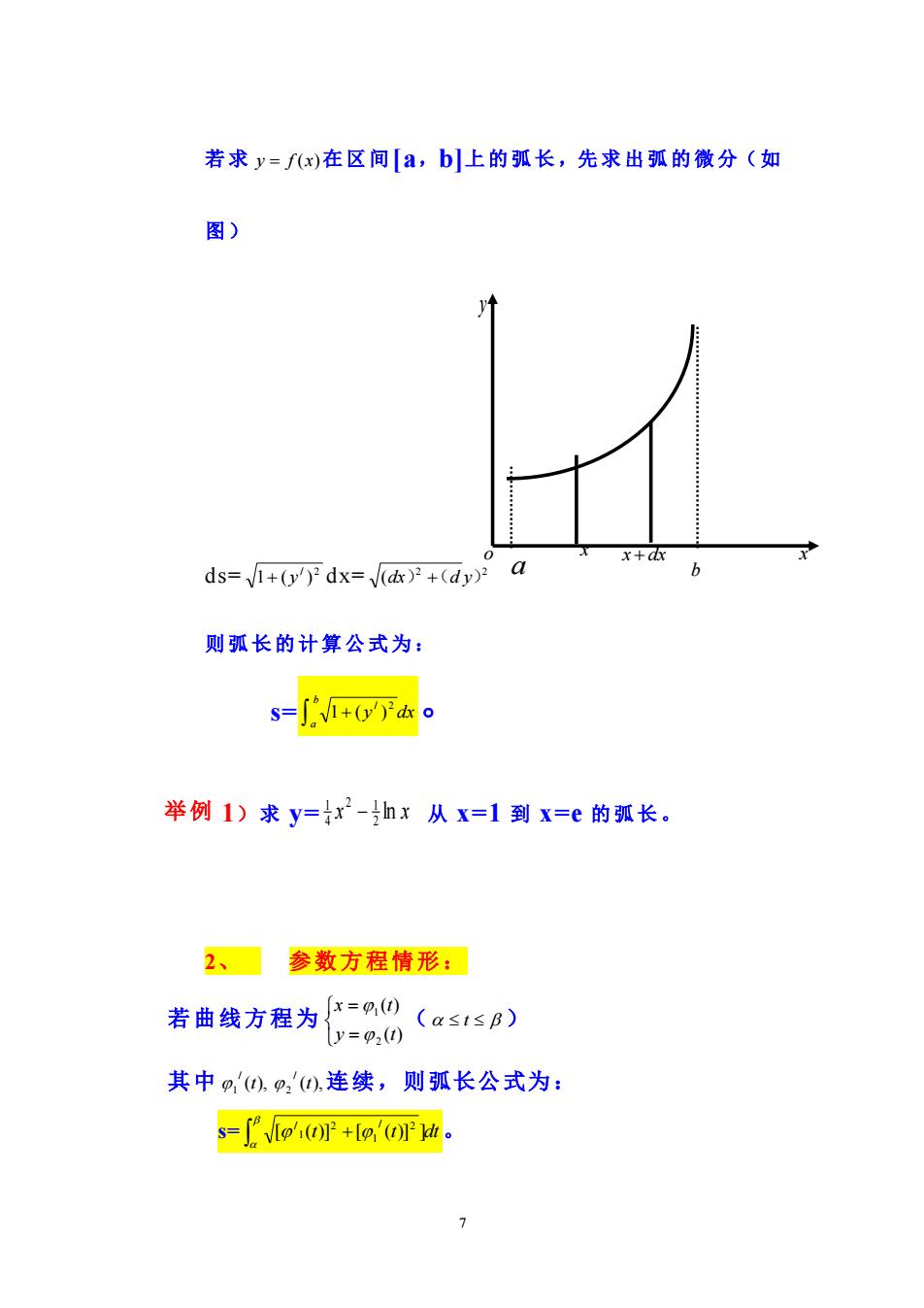
若求y=fx)在区间[a,b]上的弧长,先求出弧的微分(如 图) ds=+dx=(d)a x+ax 则弧长的计算公式为: s=∫+0To 举例1)求y=x2-hx从x=1到x=e的弧长。 2、参数方程情形: 若曲线方程为任=0(a≤1≤B) y=p2() 其中o,'),p,'),连续,则弧长公式为: s=Vo+gPh
7 若 求 y = f (x) 在区间 [a,b]上 的 弧 长 ,先 求 出 弧 的 微 分( 如 图 ) ds= / 2 1+ ( y ) dx= 2 2 (dx) +(d y) 则弧长的计算公式为: s= y dx b a + / 2 1 ( ) 。 举例 1) 求 y= x ln x 2 2 1 4 1 − 从 x=1 到 x=e 的弧长 。 2、 参数方程情形: 若曲线方程为 = = ( ) ( ) 2 1 y t x t ( t ) 其中 ( ), / 1 t ( ), / 2 t 连续,则弧长公式为: s= t t dt + [ ( )] [ ( )] ] / 2 1 2 1 / 。 a b o x x dx + x y

举例2)求圆x2+y2=R2的周长。 举例3)求摆线=1-s血)(0≤1s2x)一拱的长度。 y=a(1-cost) (B)、极坐标下的弧长公式 设曲线弧的极坐标方程为:p=p(),a≤0≤B 且p()存在连续的导数,则弧长计算公式为 s-e(O)J+[e(0)Jdo .x=p()cos8 y=P(O)sin9a≤0sp ∴.d=V)°+(d)'=-=p()]+[p(0)]d0 举例4)求心形线p=a1+cos0),(0≤0≤2r)的全长 +()=-=an+coso -2a+cos0d0-2acosd0-8a 作业:286页21
8 举例 2)求 2 2 2 圆x y R + = 的周长。 举例 3)求 摆 线 = − = − (1 cos ) ( sin ) y a t x a t t ( 0 t 2 )一拱 的长度 。 (B)、极坐标下的弧长公式 设曲线弧的极坐标方程为 : = ( ) , 且 ( ) 存在连续的导数,则弧长计算公式为 ( ) ( ) 2 2 ' s d = + ( ) ( ) cos sin x y = = ( ) ( ) 2 2 = + ds dx dy =-= ( ) ( ) 2 2 ' + d 举 例 4) 求心形线 = + a(1 cos ) ,( 0 2 )的全长 ( ) 2 2 ' + = − − −− = + 2 1 cos a 0 0 2 2 1 cos 2 2 2 cos 8 2 s a d a d a = + = = 作业: 286 页 21

§6-3物理方面的应用 (The application of physics) (一)、变力沿直线所作的功 (常力直镜作功中学W=Fs,变力曲线作功团)曲线积 分内容介绍) 设物体在变力F=f(x)的作用下,沿x轴从a移到b,且力 的方向与X轴正向一致,由微元法知道,在x,X+dx上功的徽分 为:dw=f(x)dx。于是,变力对物体所作的功为: w=[f(x)dr 举例(P289-一例3) 例(292页-5题) (二)、流体(水)的压力 设有一闸门为ABCD(如图所示) 当闸门全部浸在水中时,求闸门所受的压力P。 实验表明:重压(向下压力)=侧压(侧面压力) 9
9 § 6-3 物理方面的应用 ( The application of physics) (一) 、变力沿直线所作的功 (常力直线作功 ⎯中学所知 ⎯ ⎯→ w=Fs, 变 力 曲 线 作 功 ⎯下册⎯→ 曲线积 分内容 介绍) 设 物 体 在 变力 F=f(x)的作 用 下,沿 x 轴从 a 移到 b,且 力 的方向与 x 轴正 向 一 致, 由 微元 法 知 道, 在 [x,x+dx]上 功 的微 分 为 : dw=f( x) dx。于是,变力对物体所作的功为 : w= b a f (x)dx 举 例 ( P289— — 例 3) 例 ( 292 页 -5 题 ) (二)、流体(水)的压力 设有一闸门为 ABCD(如图所示) 当闸门全部浸在水中时,求闸门所受的压力 P。 实验表明:重压(向下压力 ) =侧压 ( 侧 面压 力 )

且:压力=压强(单位面积压力)×受压面积 在水深为x处的压强Q=rx(r为水的比重:r=1000公斤/m) 因此,在[x,x+dx]中小曲边梯形的面积近似为:f(x)dx 压力的微分为:dp=Qf(x)dx=rxf(x)dx 于是,整个闸门(一侧)的压力为: P=rxf(x)dx 举例(P290-例4.) 举例(或P292-10习题) (三)引力*(略) 作业:292页4:8. (§6一4平怕值(略))* 一、函数的平均值 连续函数fx)在a,b上的平均值为: y=f(x)(积分中值Th:f5)上亡。心f(x)k) 二、均方根
10 且:压力 =压强(单位面积压力) 受压面积 在水深为 x 处的压强 Q=rx (r 为水的比重: r=1000 公 斤 /m 3 ) 因此,在 [x, x+dx]中 小 曲 边 梯 形 的面 积 近似 为 : f(x)dx 压力的微分为: dp=Qf(x)dx=rxf(x)dx 于 是 , 整 个 闸门 (一 侧)的 压力 为: P= b a rxf (x)dx 举例( P290-例 4. ) 举 例 ( 或 P292-10 习题) (三)引力*(略) 作业:292 页 4;8. (§6—4 平均值(略))* 一、 函数的平均值 连续函数 f(x)在[a,b]上的平均值为: − − = b a b a y f (x)dx 1 ( 积分中值 Th: f( )= − b a b a f (x)dx 1 ) 二、均方根