
第六章数学棋型 教学目标: 1、学会利用数学的极限知识解决复利、抵押贷款问题: 2、了解基本经济函数及对应的经济意义: 3、学会利用导数知识对经济函数进行边际、弹性分析,并理解其 经济意义: 6.1经济学模型 6.1.1经济的极限棋型 一复利问题 【讲授】复利是计算利息的一种方法。复利是指不仅对本金计算利息, 而且要计算利息的利息。即本期的本金加上利息作为下期计算利息的 基数,俗称“利滚利”。 设A是本金,r是计息期的利率,1是计息期数,A是本利和。 【创建模型】 第一个计息期末的本利和:A=A,1+r) 第二个计息期末的本利和: A=A1+r)+[A1+r乃=A1+r2 第三个计息期末的本利和: A=A,0+r}+A+r}}=A1+r月 第1个计息期末的本利和:A=A,1+r (1)
1 第六章 数学模型 教学目标: 1、学会利用数学的极限知识解决复利、抵押贷款问题; 2、了解基本经济函数及对应的经济意义; 3、学会利用导数知识对经济函数进行边际、弹性分析,并理解其 经济意义; 6.1 经济学模型 6.1.1 经济的极限模型 一 复利问题 【讲授】复利是计算利息的一种方法。复利是指不仅对本金计算利息, 而且要计算利息的利息。即本期的本金加上利息作为下期计算利息的 基数,俗称“利滚利”。 设 A0 是本金, r 是计息期的利率, t 是计息期数, A 是本利和。 【创建模型】 第一个计息期末的本利和: A = A (1+ r) 0 第二个计息期末的本利和: ( ) ( ) ( ) 2 A = A0 1+ r + A0 1+ r r = A0 1+ r 第三个计息期末的本利和: ( ) ( ) ( ) 3 0 2 0 2 A = A0 1+ r + A 1+ r r = A 1+ r . 第 t 个计息期末的本利和: ( ) t A = A 1+ r 0 (1)

【结论】若每期结算m次,则每期的利率为二,可推出第1期末的本 利和为 (2) 【结论】若每期结算次数m→0(即每时每刻结算)时,第1期末的 本利和为 A=Ape" (3) 公式(1)入、(2)称为离散复利公式,公式(3)称为连续复利公式。其 中A称为现值,A称为终值。显然,公式(3)的计算结果比公式(1)、 (2)的计算结果要大些。 【板演】例1先将10000元现金存入银行,年利率1.98%,分别用离 散复利公式和连续复利公式计算10年末的本利和(不扣利息税)。 解将A=10000,r=1.98%,t=10代入公式A=A,(1+r、 A=Ae"中,得 离散复利公式计算结果表示以一年结算一次,10年末的本利和 A=100001+0.0198°≈121.66元 连续复利公式得10年末的本利和 A=10000e0019810≈121.90元 2
2 【结论】若每期结算 m 次,则每期的利率为 m r ,可推出第 t 期末的本 利和为 mt m r A A = 0 1+ (2) 【结论】若每期结算次数 m→ (即每时每刻结算)时,第 t 期末的 本利和为 rt mt m mt m A e m r A m r A A0 0 1 0 lim 1 lim = = + = + → → 即 rt A A e = 0 (3) 公式(1)、(2)称为离散复利公式,公式(3)称为连续复利公式。其 中 A 称为现值, A0 称为终值。显然,公式(3)的计算结果比公式(1)、 (2)的计算结果要大些。 【板演】例 1 先将 10000 元现金存入银行,年利率 1.98%,分别用离 散复利公式和连续复利公式计算 10 年末的本利和(不扣利息税)。 解 将 A0 =10000,r =1.98%,t =10 代 入 公 式 ( ) t A = A 1+ r 0 、 rt A A e = 0 中,得 离散复利公式计算结果表示以一年结算一次,10 年末的本利和 10000(1 0.0198) 121.66 10 A = + 元 连续复利公式得 10 年末的本利和 10000 121.90 0.0198 10 = A e 元

【板演】例2某厂1990年的产值1000万元,2010年末产值翻两番, 利用连续复利公式求每年的平均增长率。 解将A=4000,A。=1000,t=20代入公式A=Ae"中,得 4000=1000e2r三4=e20r→n4=20rhe-20r=2n2→r=6.93% 二抵押贷款问题 【讲授】问题:设某商品房的价值100000元,王某自己积蓄有40000 元,余款需贷款。贷款的月利率1%,需每月还款,25年还清。假如还 不起,房子归债权人银行。分析银行根据什么判断王某具有贷款资格。 分析问题条件:贷款额60000元,月利率r=1%,贷款时间 25×12=300月。每月还x元,yn表示第n个月欠银行的钱。 【创建模型】分析问题过程: %=60000 y=1+r)-x y=y1+r)x=%1+r}-x[+r)+ 为=y01+r-x=%1+月-x1+}+0+)+可 y=y(1+r)-x=%(0+r”-x0+r++(0+r+(+r)+1 %*+少-] 3
3 【板演】例 2 某厂 1990 年的产值 1000 万元,2010 年末产值翻两番, 利用连续复利公式求每年的平均增长率。 解 将 A = 4000, A0 =1000,t = 20 代入公式 rt A A e = 0 中,得 4000 1000 4 ln 4 20 ln 20 2ln 2 6.93% 2 2 0 = e = e = r e r = r = o r r 二 抵押贷款问题 【讲授】问题:设某商品房的价值 100000 元,王某自己积蓄有 40000 元,余款需贷款。贷款的月利率 1%,需每月还款,25 年还清。假如还 不起,房子归债权人银行。分析银行根据什么判断王某具有贷款资格。 分析问题条件:贷款额 60000 元,月利率 r = 1%,贷款时间 2512 = 300 月。每月还 x 元, n y 表示第 n 个月欠银行的钱。 【创建模型】分析问题过程: y0 = 60000 y = y (1+ r)− x 1 0 (1 ) (1 ) (1 ) 1 2 y2 = y1 + r − x = y0 + r − x + r + (1 ) (1 ) (1 ) (1 ) 1 3 2 y3 = y2 + r − x = y0 + r − x + r + + r + . ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 0 0 1 1 1 1 1 1 1 1 1 n n n n n n y y r x y r x r r r x r y r r − − = + − = + − + + + + + + + + − = + +

当贷款还清时,上.=0,得x=+ 1+r”-1 。将6=60000元, 月利率r=1%,贷款时间n=300月代入上式,得x≈631.93元。 结论,只要王某每月不具有631.93的还贷能力银行就不能贷款。 6.1.2常见经济函数 一需求函数与供给函数 【讲解】一个商品在市场上的需求有许多影响因素,其中主要是与 它的价格有关系,价格贵,需求量就少,价格便宜,买的人就多。 需求和价格之间可以把它简化为一种函数关系。我们先不考虑其它 因素,简单地认为价格定了需求量就随之确定,这样需求量就是价 格的函数。供给,就是厂方能够为市场提供多少产品,当然它也是 和价格有关系的,产品价格高,厂方就增加生产,反之供给量就减 少。我们也可以把它简化为一种函数关系。需求量与价格之间的函 数就称为需求函数,供给量与价格之间的函数就称为供给函数。 【板演】如果需求函数和供给函数都是线性函数(一次函数),在 这种关系下,通过讨论看可以得到什么性质。 2=a-bp (a)0.b)0) Q表示需求量,P表示价格,a,b表示常数。(如图6.1.1) S=cp-d (c)0,d)0) S表示供给量,P表示价格,c,d表示常数。(如图6.1.2) 4
4 当贷款还清时, yn = 0 ,得 ( ) (1 ) 1 0 1 + − + = n n r y r r x 。将 y0 = 60000 元, 月利率 r = 1%,贷款时间 n = 300 月代入上式,得 x 631.93 元。 结论,只要王某每月不具有 631.93 的还贷能力银行就不能贷款。 6.1.2 常见经济函数 一 需求函数与供给函数 【讲解】一个商品在市场上的需求有许多影响因素,其中主要是与 它的价格有关系,价格贵,需求量就少,价格便宜,买的人就多。 需求和价格之间可以把它简化为一种函数关系.我们先不考虑其它 因素,简单地认为价格定了需求量就随之确定,这样需求量就是价 格的函数。供给,就是厂方能够为市场提供多少产品,当然它也是 和价格有关系的,产品价格高,厂方就增加生产,反之供给量就减 少。我们也可以把它简化为一种函数关系。需求量与价格之间的函 数就称为需求函数,供给量与价格之间的函数就称为供给函数。 【板演】如果需求函数和供给函数都是线性函数(一次函数),在 这种关系下,通过讨论看可以得到什么性质。 Q = a − bp (a0,b0) Q 表示需求量, p 表示价格, a , b 表示常数。(如图 6.1.1) S = cp − d (c0,d0) S 表示供给量, p 表示价格, c, d 表示常数。(如图 6.1.2)
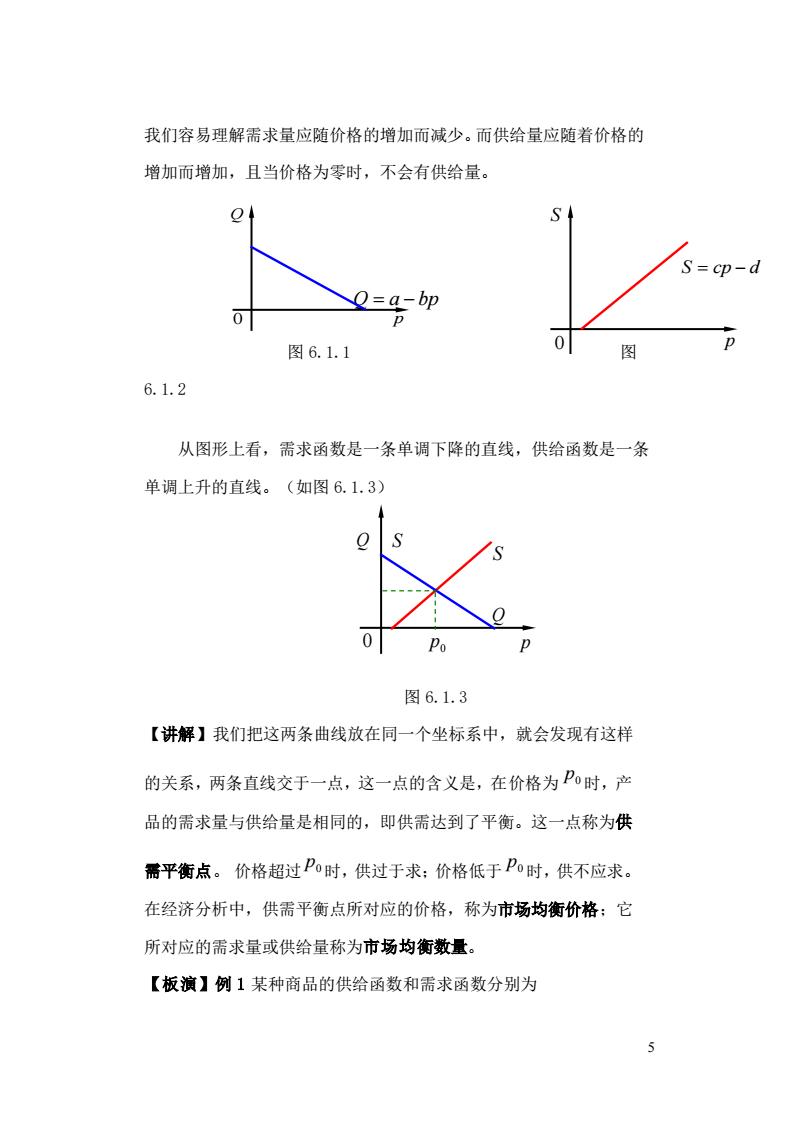
我们容易理解需求量应随价格的增加而减少。而供给量应随着价格的 增加而增加,且当价格为零时,不会有供给量。 S =cp-a O=a-bp 0 D 图6.1.1 0 6.1.2 从图形上看,需求函数是一条单调下降的直线,供给函数是一条 单调上升的直线。(如图6.1.3) 0 0 Po D 图6.1.3 【讲解】我们把这两条曲线放在同一个坐标系中,就会发现有这样 的关系,两条直线交于一点,这一点的含义是,在价格为P时,产 品的需求量与供给量是相同的,即供需达到了平衡。这一点称为供 需平衡点。价格超过P0时,供过于求:价格低于P0时,供不应求。 在经济分析中,供需平衡点所对应的价格,称为市场均衡价格:它 所对应的需求量或供给量称为市场均衡数量。 【板演】例1某种商品的供给函数和需求函数分别为
5 我们容易理解需求量应随价格的增加而减少。而供给量应随着价格的 增加而增加,且当价格为零时,不会有供给量。 图 6.1.1 图 6.1.2 从图形上看,需求函数是一条单调下降的直线,供给函数是一条 单调上升的直线。(如图 6.1.3) 图 6.1.3 【讲解】我们把这两条曲线放在同一个坐标系中,就会发现有这样 的关系,两条直线交于一点,这一点的含义是,在价格为 0 p 时,产 品的需求量与供给量是相同的,即供需达到了平衡。这一点称为供 需平衡点。 价格超过 0 p 时,供过于求;价格低于 0 p 时,供不应求。 在经济分析中,供需平衡点所对应的价格,称为市场均衡价格;它 所对应的需求量或供给量称为市场均衡数量。 【板演】例 1 某种商品的供给函数和需求函数分别为 Q = a − bp Q 0 p S = cp − d S 0 p 0 Q p S 0 p Q S

S=25p-10 0=200-5p 求该商品的市场均衡价格和市场均衡数量 解:由市场均衡条件Q=S,得到 25p-10=200-5p 解出 P=7,9=165 二其它经济函数 (一)成本函数 【讲解】一种产品的成本可以分为两部分:固定成本C。,比如, 生产过程中的设备投资,或使用的工具,不管生产产品与否,这些 费用都是要有的,它是不随产量而变化的,这种成本称为固定成本。 变动成本C,比如每一件产品的原材料,这些费用依赖于产品的 数量,这种成本称为变动成本。 总成本就是固定成本加上变动成本 C=Co+C 成本应与产品的产量有关,这种函数表示为 C(q)=C。+C,(q) 6
6 Q = 200 − 5 p 求该商品的市场均衡价格和市场均衡数量. 解:由市场均衡条件 Q = S ,得到 25p −10 = 200 − 5p 解出 p0 = 7 , q0 = 165 二 其它经济函数 (一) 成本函数 【讲解】一种产品的成本可以分为两部分:固定成本 C0 ,比如, 生产过程中的设备投资,或使用的工具,不管生产产品与否,这些 费用都是要有的,它是不随产量而变化的,这种成本称为固定成本。 变动成本 C1, 比如每一件产品的原材料,这些费用依赖于产品的 数量,这种成本称为变动成本。 总成本就是固定成本加上变动成本 C = C0 +C1 成本应与产品的产量有关,这种函数表示为 ( ) ( ) C q = C0 +C1 q S = 25 p −10

这就是成本函数.其中总成本C(q)是产量q的函数,C。与产 量无关,变动成C(q)也是产量q的函数。 我们再引入平均成本的概念 C=C(q) 总成本除以产量g,就是产量为q时的平均成本,用C来表示。 (二)收入函数 【讲解】下面我们来讲收入函数。一种产品销售之后就会有销售收 入,销售收入应该是价格乘以产量。但价格与产量之间也有一定的 关系,这样就得到 R=q.p(q) 其中()是价格与产量之间的函数关系。相应地有平均收入函数 R=Rq) 现在我们来研究一种最简单的情况,把收入看作产量的线性 函数(价格不随产量而变化),也就是 R=p.q 它的图形就是下面这样(如图6.1.4)。 0
7 这就是成本函数.其中总成本 C(q) 是产量 q 的函数,C0 与产 量无关,变动成 ( ) C1 q 也是产量 q 的函数。 我们再引入平均成本的概念 q C q C ( ) = 总成本除以产量 q ,就是产量为 q 时的平均成本,用 C 来表示。 (二)收入函数 【讲解】下面我们来讲收入函数。一种产品销售之后就会有销售收 入,销售收入应该是价格乘以产量。但价格与产量之间也有一定的 关系,这样就得到 R = q p(q) 其中 p(q)是价格与产量之间的函数关系。相应地有平均收入函数 q R q R ( ) = 现在我们来研究一种最简单的情况,把收入看作产量的线性 函数(价格不随产量而变化),也就是 R = p q 它的图形就是下面这样(如图 6.1.4)。 O q

图6.1.4 图形说明销售数量越多收入越多,这是一条单调增加的直线。 (三)利润函数 【讲解】还有一个函数就是利润函数大家也容易理解,因为在收入 中减去成本得到的就是利润。既然成本是产量q的函数,收入也是 q的函数,那么利润也是g的函数。即 L(a)=R(a)-c(a) 相应的有平均利润函数的概念 D=(g刨 (1)L(g)>0盈利: (2)L(g)<0亏损: (3)L(g)=0盈亏平衡。 满足L(g)=0的%称为盈亏平衡点(又称保本点)。 在假设成本函数和收入函数都是线性函数的情况下来做一些 分析: C=Co+cq R=p.q 它们的图形是(如图6.1.5)
8 图 6.1.4 图形说明销售数量越多收入越多,这是一条单调增加的直线。 (三)利润函数 【讲解】还有一个函数就是利润函数大家也容易理解,因为在收入 中减去成本得到的就是利润。既然成本是产量 q 的函数,收入也是 q 的函数,那么利润也是 q 的函数。即 L(q) = R(q) − C(q) 相应的有平均利润函数的概念 q L q L ( ) = (1) L(q) > 0 盈利; (2) L(q) < 0 亏损; (3) L(q) = 0 盈亏平衡。 满足 L(q) = 0 的 q0 称为盈亏平衡点(又称保本点)。 在假设成本函数和收入函数都是线性函数的情况下来做一些 分析: C = c0 + cq R = p q 它们的图形是(如图 6.1.5)
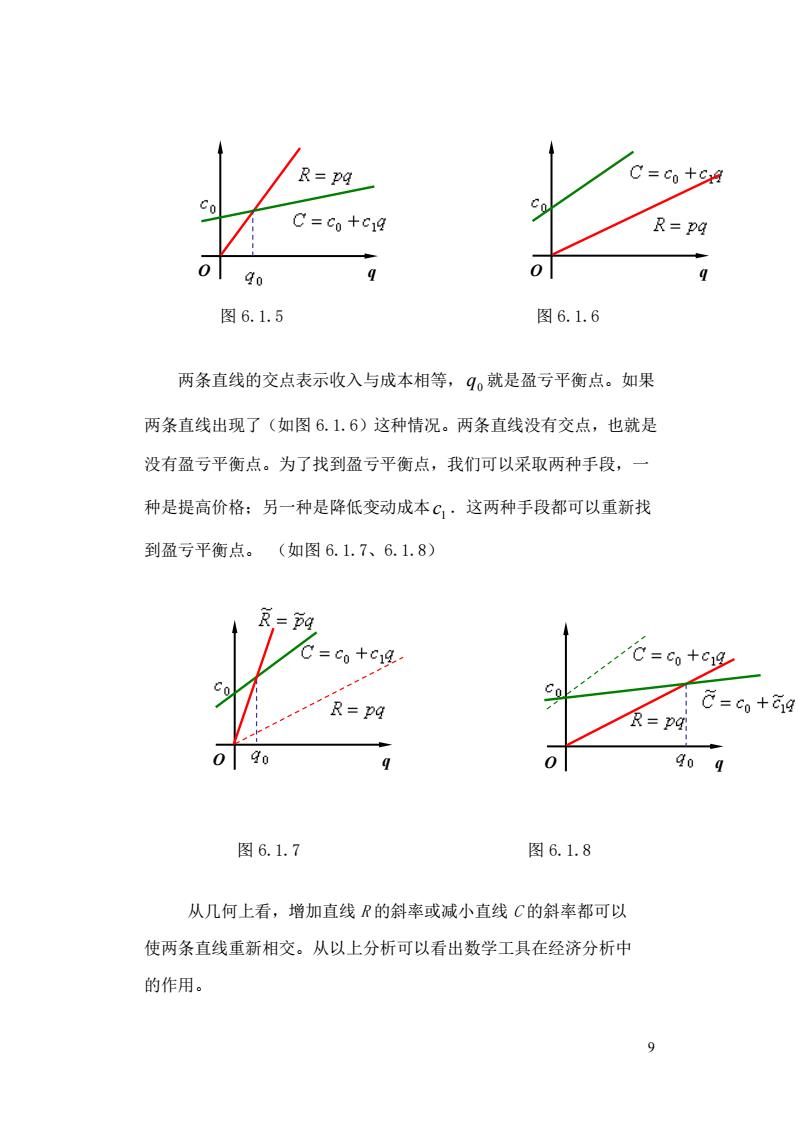
R=p4 C=Co+4 C=Co+c1q R=pq 0 90 0 图6.1.5 图6.1.6 两条直线的交点表示收入与成本相等,9就是盈亏平衡点。如果 两条直线出现了(如图6.1,6)这种情况。两条直线没有交点,也就是 没有盈亏平衡点。为了找到盈亏平衡点,我们可以采取两种手段,一 种是提高价格:另一种是降低变动成本C1·这两种手段都可以重新找 到盈亏平衡点。(如图6.1.7、6.1.8) R.=pg C=co+C1g C=co+c1g R=pq C=co+619 0 9q 图6.1.7 图6.1.8 从几何上看,增加直线R的斜率或减小直线C的斜率都可以 使两条直线重新相交。从以上分析可以看出数学工具在经济分析中 的作用。 9
9 图 6.1.5 图 6.1.6 两条直线的交点表示收入与成本相等, 0 q 就是盈亏平衡点。如果 两条直线出现了(如图 6.1.6)这种情况。两条直线没有交点,也就是 没有盈亏平衡点。为了找到盈亏平衡点,我们可以采取两种手段,一 种是提高价格;另一种是降低变动成本 1 c .这两种手段都可以重新找 到盈亏平衡点。 (如图 6.1.7、6.1.8) 图 6.1.7 图 6.1.8 从几何上看,增加直线 R 的斜率或减小直线 C 的斜率都可以 使两条直线重新相交。从以上分析可以看出数学工具在经济分析中 的作用。 O q O q O q O q

【板演】例3生产某商品的总成本是 C(q)=500+2q 求生产50件商品时的总成本和平均成本。 解:成本 C(q)=500+2g C(50)=500+2×50=600 平均成本 cg)-C@.500+29.500+2 9 C(50)=50 +2=12 50 【板演】例4某商品的成本函数与收入函数分别为 C=21+5q R=8g 求该商品的盈亏平衡点。 解 C(q)=21+5g R(g)=8q C(q)=R(q) 21+5q=8g 9=7 6.1.3经济的导数模型 10
10 【板演】例 3 生产某商品的总成本是 C(q) = 500 + 2q 求生产 50 件商品时的总成本和平均成本。 解:成本 C(q) = 500 + 2q C(50) = 500 + 250 = 600 平均成本 2 ( ) 500 2 500 ( ) = + + = = q q q q C q C q 2 12 50 500 C (50) = + = 【板演】例 4 某商品的成本函数与收入函数分别为 C = 21+ 5q R = 8q 求该商品的盈亏平衡点。 解: C(q) = 21+ 5q R(q) = 8q C(q) = R(q) 21+ 5q = 8q q = 7 6.1.3 经济的导数模型