
换元积分法 直接利用基本积分表和分项积分法所能计算的 不定积分是非常有限的,为了求出更多的积分,需 要引进更多的方法和技巧本节和下节就来介绍求积 分的两大基本方法—换元积分法和分部积分法。 在微分学中,复合函数的微分法是一种重要的 方法,不定积分作为微分法的逆运算,也有相应 的方法。利用中间变量的代换,得到复合函数的 积分法一换元积分法。通常根据换元的先后, 把换元法分成第一类换元和第二类换元
换元积分法 直接利用基本积分表和分项积分法所能计算的 不定积分是非常有限的,为了求出更多的积分,需 要引进更多的方法和技巧本节和下节就来介绍求积 分的两大基本方法——换元积分法和分部积分法。 在微分学中,复合函数的微分法是一种重要的 方法,不定积分作为微分法的逆运算,也有相应 的方法。利用中间变量的代换,得到复合函数的 积分法——换元积分法。通常根据换元的先后, 把换元法分成第一类换元和第二类换元

一、第一类换元法 问题 ∫cos2.xk4sin2x+C, 解决方法 利用复合函数,设置中间变量, 过程 令t=2x→d=5t, ∫cos2xc=打cos抽=2int+C=2sin2x+C sin2x+CT=cos2x 说明结果正确
问题 cos2xdx= sin2x + C, 解决方法 利用复合函数,设置中间变量. 过程 令 t = 2x , 2 1 dx = dt cos2xdx tdt = cos 2 1 = sint + C 2 1 sin2 . 2 1 = x + C 一、第一类换元法 sin 2x C] cos 2x 2 1 [ + = 说明结果正确

将上例的解法一般化: 设F'(u)=f(w),则f(u)du=F(w+C. 如果u=p(x)(可微) dFlo(x)1=flo(x)lo'(x)d ∴.JfLp(x)p'(x)k=F[p(x川+C =f(u)dul) 将上述作法总结成定理,使之合法化,可得 换元法积分公式
将上例的解法一般化: 设 F(u) = f (u), 则 ( ) ( ) . f u du = F u + C 如果 u = (x) (可微) dF[(x)] = f[(x)](x)dx f[(x)](x)dx = F[(x)]+ C = = ( ) [ ( ) ] u du u x f 将上述作法总结成定理,使之合法化,可得 ——换元法积分公式

定理1设f(W)具有原函数,u=p(x)可导, 则有换元公式 [f(x)'(x)dx=If(u)dul 第一类换元公式(凑微分法) 说明 使用此公式的关键在于将 ∫g(x)d化为fIp(x)lp'(x)d. 观察重点不同,所得结论不同
设 f (u)具有原函数, f[(x)](x)dx = = ( ) [ ( ) ] u du u x f 第一类换元公式(凑微分法) 说明 使用此公式的关键在于将 g(x)dx 化为 [ ( )] ( ) . f x x dx 观察重点不同,所得结论不同. u = (x)可导, 则有换元公式 定理1

注① 定理说明:若已知「f(u)du=F(w)+C 则」fIp(x)p'(x)=F[p(x)川+C 因此该定理的意义就在于把 f(w)du=F(w)+C中的u换成另一个 x的可微函数p(x)后,式子仍成立 —又称为积分的形式不变性 这样一来,可使基本积分表中的积分公式 的适用范围变得更加广泛。 ②由定理可见,虽然JfIp(x)p'(x) 是一整体记号,但可把x视为自变量微分 →p'(x)k=do(x) 凑微分
注 ① 定理说明:若已知 f (u)du = F(u) + C 则 f x x dx = F x + C [( )] ( ) [( )] 因此该定理的意义就在于把 f (u)du = F(u) + C 中的 u 换成另一个 x 的可微函数 (x) 后,式子仍成立 ——又称为积分的形式不变性 这样一来,可使基本积分表中的积分公式 的适用范围变得更加广泛。 dx ②由定理可见,虽然 f[(x)](x)dx 是一整体记号,但可把 视为自变量微分 (x)dx = d(x) ——凑微分

③凑微分法就在凑微分上,其基本思想就是对被积 表达式进行变形,主要考虑如何变化f(x)水 凑微分法的基本思路: 与基本积分公式相比较,将不同的部分 中间变量和积分变量— 变成相同 步骤:凑微分;换元求出积分;回代原变量 例1求sin2xdk. 解(一)jsin2x=sin2xd(2x) cos2.x+C;
③凑微分法就在凑微分上,其基本思想就是对被积 表达式进行变形,主要考虑如何变化 f (x)dx 凑微分法的基本思路: 与基本积分公式相比较,将不同的部分—— 中间变量和积分变量——变成相同 步骤:凑微分;换元求出积分;回代原变量 例1 求 sin2 . xdx 解(一) sin2xdx = sin2 (2 ) 2 1 xd x cos 2 ; 2 1 = − x + C
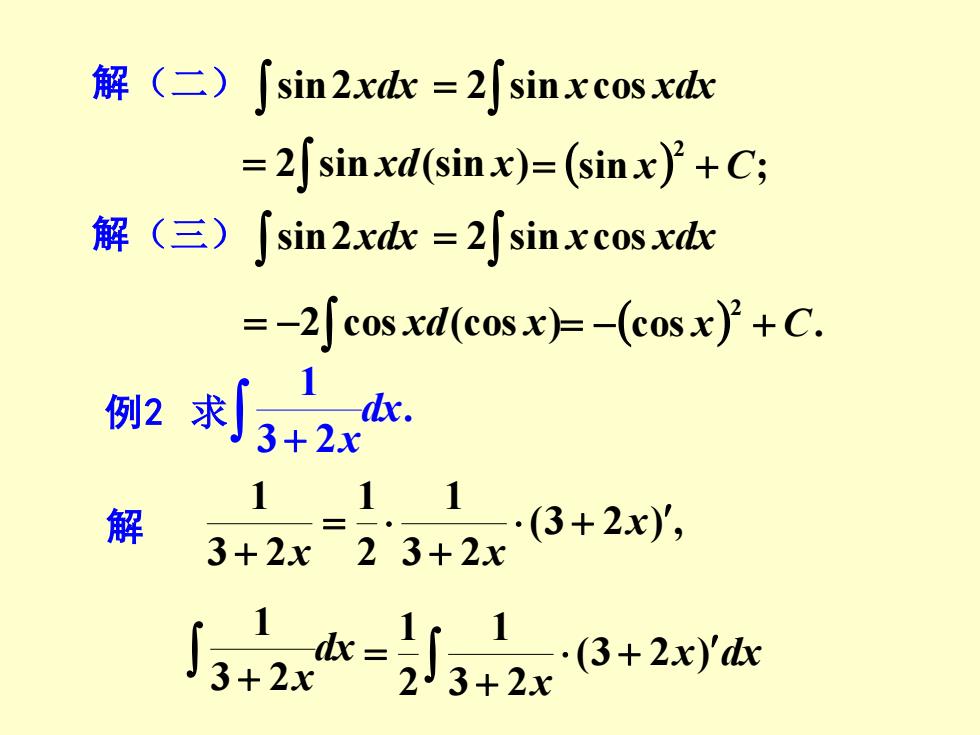
解(二)∫sin2xdk=2∫sinxcosxd =2Jsinxd(sinx)=(sinx)+C; 解(三)∫sin2xdk=2 sin xcosxo =-2fcosxd(cosx)=-(cosx)+C. 232盒 解 1=1.1-(3+2xy, 3+2x23+2x 3+2=32x0+2xy
解(二) sin2xdx = 2 sin xcos xdx = 2 sin xd(sin x) (sin ) ; 2 = x + C 解(三) sin2xdx = 2 sin xcos xdx = − 2 cos xd(cos x) (cos ) . 2 = − x + C 例2 求 . 3 2 1 dx x + 解 (3 2 ) , 3 2 1 2 1 3 2 1 + + = + x x x dx x 3 + 2 1 x dx x (3 2 ) 3 2 1 2 1 + + =
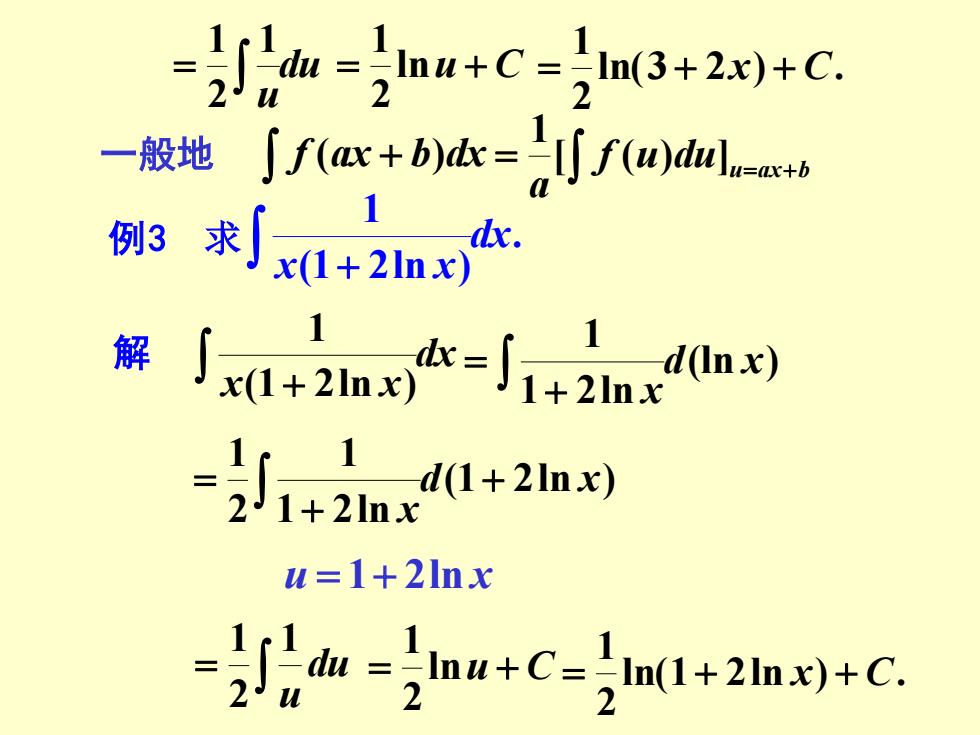
-打-ua+C=(3+2+C 一般地 ∫f(ax+b)c=f(w)du-+b 附求灯ka+2nc 解ju+2nr-j1+2nd0a 1+2n1+2n0 u=1+2Inx =打a=nu+c-n1+2na)+c
du u = 1 2 1 = lnu + C 2 1 ln(3 2 ) . 2 1 = + x + C f (ax + b)dx = u du u=ax+b f a [ ( ) ] 1 一般地 例3 求 . (1 2ln ) 1 dx x x + 解 dx x x (1+ 2ln ) 1 (ln ) 1 2ln 1 d x x + = (1 2ln ) 1 2ln 1 2 1 d x x + + = u = 1+ 2ln x = du u 1 2 1 = lnu + C 2 1 ln(1 2ln ) . 2 1 = + x + C

解 n4= d a+对a++刘 1 1 + +G+21++C 4*++
例4 求 . (1 ) 3 dx x x + 解 dx x x + 3 (1 ) dx x x + + − = 3 (1 ) 1 1 ] (1 ) (1 ) 1 (1 ) 1 [ 2 3 d x x x + + − + = 1 2 2 2(1 ) 1 1 1 C x C x + + + + + = − . 2(1 ) 1 1 1 2 C x x + + + + = −
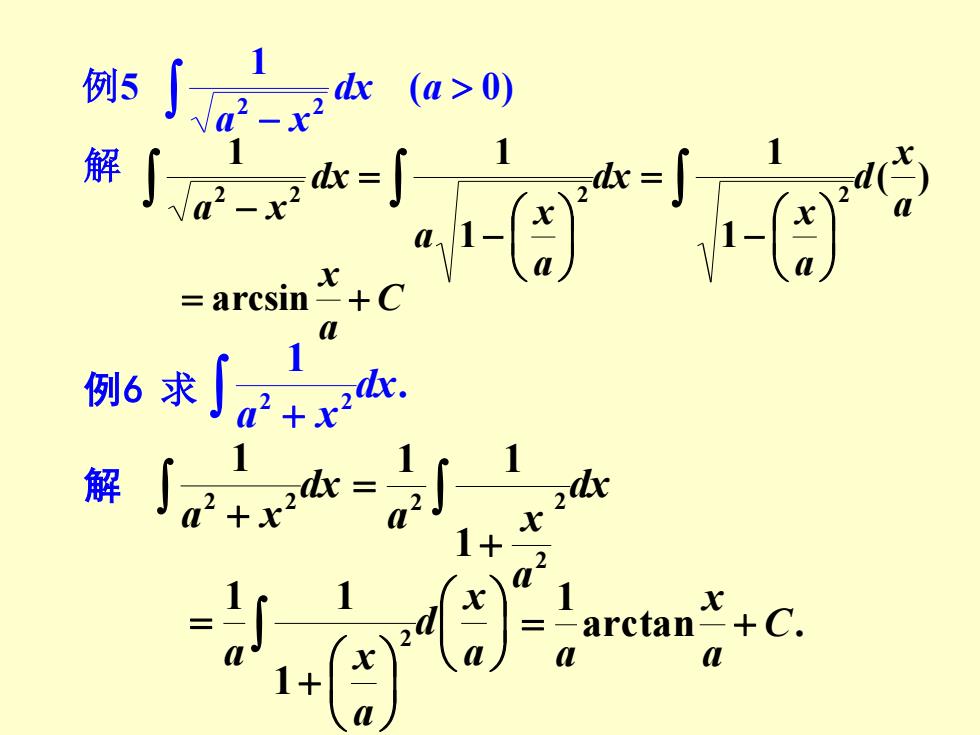
例5 ∫-xa>0 eo 解 arcsin 6求∫十、 dx =arctan+C. L
例5 − ( 0) 1 2 2 dx a a x 解 − = − dx a x a dx a x 2 2 2 1 1 1 ( ) 1 1 2 a x d a x − = C a x = arcsin + 例6 求 . 1 2 2 dx a x + 解 dx a x + 2 2 1 dx a a x + = 2 2 2 1 1 1 + = a x d a a x 2 1 1 1 arctan . 1 C a x a = +