L.Hospital法则 在第一章中我们已经知道,当分子分母都是无穷小 或都是无穷大时,两个函数之比的极限可能存在也可 能不存在,即使极限存在也不能用“商的极限等于极 限的商”这一运算法则。这种极限称为未定式「,0 0o∞ 本节我们就利用Cauchy中值定理来建立求未定式 极限的L.Hospital法则,利用这一法则,可以直接求 和0 0 这两种基本未定式的极限,也可间接求出 00 0.00,00-00,0°,00°,10 等其它类型的未定式的极限
L.Hospital法则 在第一章中我们已经知道,当分子分母都是无穷小 或都是无穷大时,两个函数之比的极限可能存在也可 能不存在,即使极限存在也不能用“商的极限等于极 限的商”这一运算法则。这种极限称为未定式 , 0 0 本节我们就利用Cauchy中值定理来建立求未定式 极限的L.Hospital法则,利用这一法则,可以直接求 和0 0 这两种基本未定式的极限,也可间接求出 0, − ,0 , ,1 0 0 等其它类型的未定式的极限

一。 型及” 型未定式解法:洛必达法则 0 定义如果当r→a(或x→∞)时,两个函数f(x) 与F(x)都趋于零或都趋于无穷大,那末极限 lim 称为或”型未定式 xa F(x) 00 x-→00 tanx In sin ax 例如, lim lim x→0 x0 Insin bx
一 、型 及 型未定式解法:洛必达法则 0 0 定义 . 0 0 ( ) ( ) lim ( ) , ( ) , ( ) ( ) 称 为 或 型未定式 与 都趋于零或都趋于无穷大 那末极限 如果当 或 时 两个函数 → → → → F x f x F x x a x f x x x a 例如, , tan lim 0 x x x→ , lnsin lnsin lim 0 bx ax x→ ) 0 0 ( ( )

定理设(①)当x→0时,函数f(x)及F(x)都趋于零 (2)在a点的某领域内点a本身可以除外,f'(x) 及F'(x)都存在且F'(x)≠0; (③)1im四存在(或为无穷大; aF(x) 那未imy lim f'(x) xa F(x) x→aF'(x) 定义这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则: 当→o时,以及x→4,x→o时,该法则仍然成立
. ( ) ( ) lim ( ) ( ) lim ( ); ( ) ( ) (3) lim ( ) ( ) 0; (2) ( ), ( ) (1) 0 , ( ) ( ) ; F x f x F x f x F x f x F x F x a a f x x f x F x x a x a x a = → → → → 那 末 存 在 或为无穷大 及 都存在且 在 点的某领域内点 本身可以除外 定理 设 当 时 函 数 及 都趋于零 定义 这种在一定条件下通过分子分母分别求导再 求极限来确定未定式的值的方法称为洛必达法则. 当x → 时,以及x → a, x → 时,该法则仍然成立

证 定义辅助函数 F(x), x≠a F()= 10, x=a 在°(a,6)内任取一点x,在以a与x为端点的区间上, f(x),F(x)满足柯西中值定理的条件, 则有 f()_f(x)-f(@f'(5) F(x)F(x)-F(a)F'(5) (5在x与a之间) 当x→a时,5→a,im9)=4img=4 a F(x) 5→aF'(5) .limf)=lim(=4. x→aF(x)5aF'(5)
证 定义辅助函数 , 0, ( ), ( ) 1 = = x a f x x a f x , 0, ( ), ( ) 1 = = x a F x x a F x ( , ) , 0 在U a 内任取一点 x 在以 a 与 x 为端点的区间上, ( ), ( ) , f 1 x F1 x 满足柯西中值定理的条件 则有 ( ) ( ) ( ) ( ) ( ) ( ) F x F a f x f a F x f x − − = ( ) ( ) F f = (在x与a之间) 当x → a时, → a, , ( ) ( ) lim A F x f x x a = → , ( ) ( ) lim A F f a = → . ( ) ( ) lim ( ) ( ) lim A F f F x f x x a a = = → →

注①定理的条件:分子分母都是无穷小;分子分母 都可导,且分母的导数不等于0;导数之比的 极限存在或为00 ②定理的结论:函数之比的极限等于导数之比的 极限 ③若im '还是未定式,且f'(x,g'(x)满足 x→g'(x) 定理中对f(x),g(x)所要求的条件,则可继续 使用法则,直到不再是未定式为止 imf()=lim f'(x) =lim f"(x) x→g(X) xx0 g(x) →g"(x)
注 ①定理的条件:分子分母都是无穷小;分子分母 都可导,且分母的导数不等于0;导数之比的 极限存在或为∞ ②定理的结论:函数之比的极限等于导数之比的 极限 ③ 使用法则,直到不再是未定式为止 定理中对 所要求的条件,则可继续 若 还是未定式,且 满足 ( ), ( ) ( ), ( ) ( ) ( ) lim 0 f x g x f x g x g x f x x x → ( ) ( ) lim ( ) ( ) lim 0 0 g x f x g x f x x x x x = → → = = → ( ) ( ) lim 0 g x f x x x

④ 将x→X换成x→x,x→x0,X→+0,x→-0, X→0 仍有类似的结论 如:x→0时型的极限 定理 设f(x),g(x)在|x>N上有定义,且 (1)lim f(x)=lim g(x)=0 K-oo K-0o (2)f(x)g(x)在|x>N时可导,且g'(x)≠0 I(x (3)lim g(x) =A或o0) 则im f(x)=lim f'(x) =A(或oo) x-→°g(x) xo g'(x)
④ → → → → → + → − + − x x x x x , x x , x , x , 将 0换成 0 0 仍有类似的结论 时 型的极限 0 0 如: x → 定理 ( ) ( ) ( ) lim ( ) ( ) lim ( ) ( ) ( ) (3)lim (2) ( ), ( ) | | ( ) 0 (1)lim ( ) lim ( ) 0 ( ), ( ) | | = = = = = → → → → → 则 或 或 在 时可导,且 设 在 上有定义,且 A g x f x g x f x A g x f x f x g x x N g x f x g x f x g x x N x x x x x

关于°型的极限,有下述定理 定理 设f(x),g(x)在x的某邻域内有定义,且 (1)lim f(x)=lim g(x)=o x→x0 x→x0 (2)f(x),g(x)可导,且g'(x)≠0 (3)lim'(x =A或o) x→xog'(x) 则im f(x)=lim f'(x) x-→wg(x)x→xg'(x) =A(或oo) 将x→X换成x→x,x→x,x→十0,x→-∞, X→0 结论仍成立
关于 型的极限,有下述定理 定理 ( ) ( ) ( ) lim ( ) ( ) lim ( ) ( ) ( ) (3) lim (2) ( ), ( ) ( ) 0 (1) lim ( ) lim ( ) ( ), ( ) 0 0 0 0 0 0 = = = = = → → → → → 则 或 或 可导,且 设 在 的某邻域内有定义,且 A g x f x g x f x A g x f x f x g x g x f x g x f x g x x x x x x x x x x x x → → → → → + → − + − x x x x x , x x , x , x , 将 0换成 0 0 结论仍成立
x3-3x+2 例1求im →1x3-x2-x+1 0) 解 原式=im 3x2-3 x13x2-2x-1 6x 3 lim x→16x-2 ex-e x-2x 例2 lim '+e-x-2 x-→0 x-sinx 0-1im x-→0 0 1-cosx ex-e-x lim lim =2 x-→0 sinx X→0 COSX 注 在反复使用法则时,要时刻注意检查是否为 未定式,若不是未定式,不可使用法则
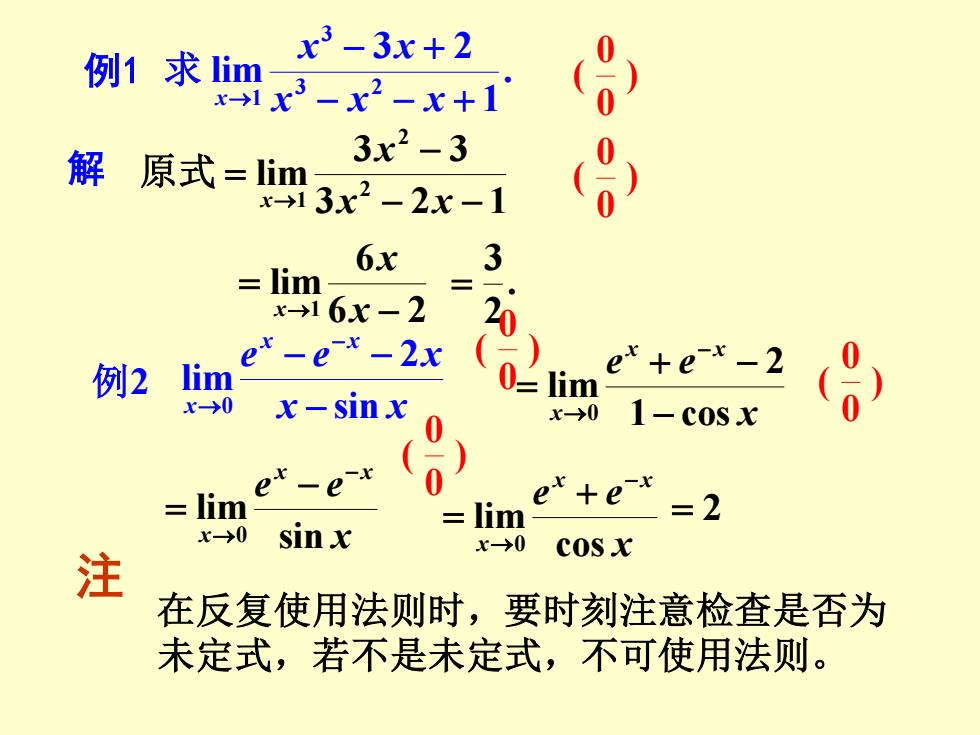
例1 . 1 3 2 lim 3 2 3 1 − − + − + → x x x x x x 求 ) 0 0 ( 解 3 2 1 3 3 lim 2 2 1 − − − = → x x x x 原式 ) 0 0 ( 6 2 6 lim 1 − = → x x x . 2 3 = 例2 x x e e x x x x sin 2 lim 0 − − − − → ) 0 0 ( x e e x x x 1 cos 2 lim 0 − + − = − → ) 0 0 ( x e e x x x sin lim 0 − → − = ) 0 0 ( x e e x x x cos lim 0 − → + = = 2 注 在反复使用法则时,要时刻注意检查是否为 未定式,若不是未定式,不可使用法则
π -arctanx 例3求im2 X-→+00 .2 解原式=lim 1 lim 七2 X→+00 x+∞1+x2 比2 例4求im Insin ax x0 Insin bx 00 解原式=im .acos·sin bx cos bx =1. x-→0bc0sbx·sinx x-→0C0SX
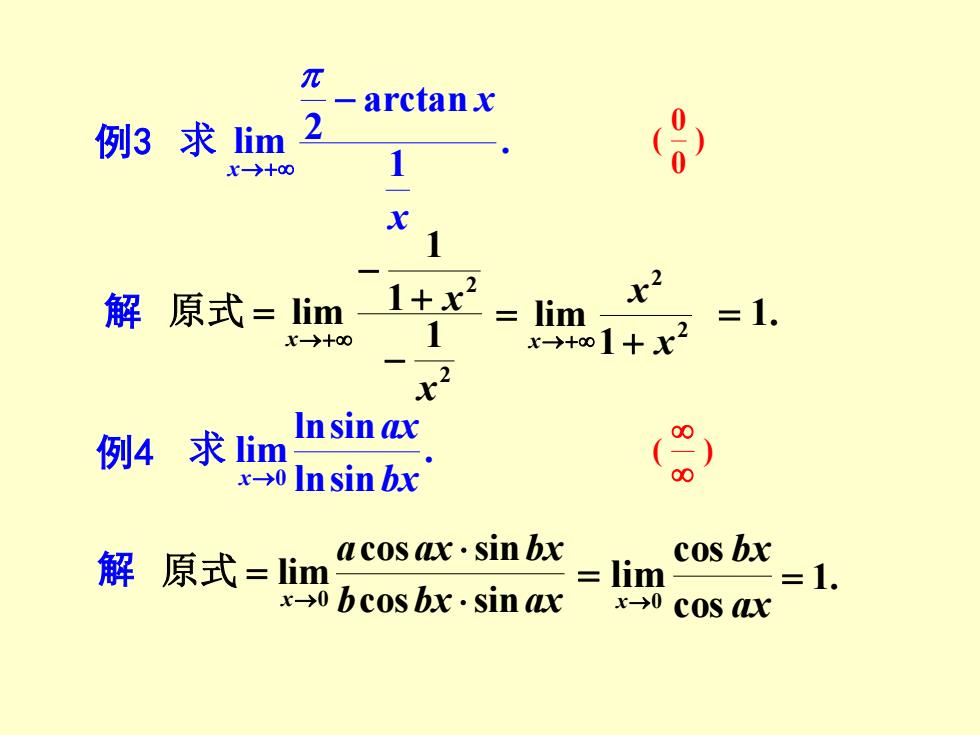
例 3 解 . 1 arctan 2 lim x x x − →+ 求 2 2 1 1 1 lim x x x − + − = →+ 原式 2 2 1 lim x x x + = →+ = 1 . 例 4 解 . lnsin lnsin lim0 bx ax x → 求 b bx ax a ax bx x cos sin cos sin lim0 = → 原式 = 1 . ) 00 (( ) ax bx x cos cos lim→0 =

例5证明im lnB=01imXx=0(B,a,u>0) x+oX“ x→+oe 证 分两种情况 ①若4=正整数则连续使用u次法则,得 x-→+o2 =0 ②若4≠正整数记u=[μ]+r(0<r<1) 则连续使用[次法则,得 me东=im44-u-+1raa A lim x→+0 Aulei =lim4(A-)(u-4+1)x 00 X→+c0 Aulei
例5 证明 0 ln lim = →+ x x x lim = 0 ( , , 0) →+ x x e x 证 分两种情况 ① 若 = 正整数 则连续使用μ次法则,得 x x x x e e x ! lim lim →+ →+ = = 0 ② 若 正整数 记 = + r (0 r 1) 则连续使用[μ]次法则,得 x x x x e x e x [ ] [ ] ( 1) ( [ ] 1) lim lim − →+ →+ − − + = x r x e x [ ] ( 1) ( [ ] 1) lim − − + = →+