
Taylor公式 多项式是一类很重要的函数,其明显特点是结构 简单,因此无论是数值计算还是理论分析都比较方便 从计算的角度看,只须加、减、乘三种运算,连除法 都不需要,这是其它函数所不具备的优点。 用多项式近似地表示给定函数的问题不仅具有实 用价值,而且更具有理论价值。一般的函数不好处理 先用较好处理的多项式近似替代,然后通过某种极限 手续再过渡到一般的函数。 “以直代曲”就是用一次多项式去近似给定函数
Taylor公式 多项式是一类很重要的函数,其明显特点是结构 简单,因此无论是数值计算还是理论分析都比较方便 从计算的角度看,只须加、减、乘三种运算,连除法 都不需要,这是其它函数所不具备的优点 。 用多项式近似地表示给定函数的问题不仅具有实 用价值,而且更具有理论价值。一般的函数不好处理 先用较好处理的多项式近似替代,然后通过某种极限 手续再过渡到一般的函数。 “以直代曲”就是用一次多项式去近似给定函数

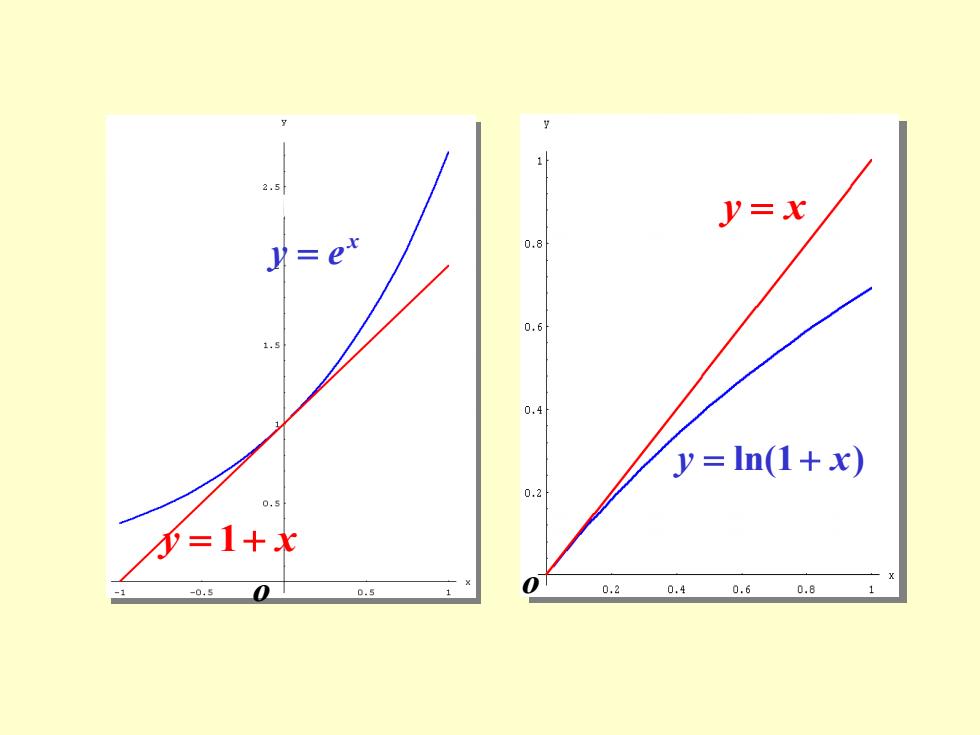
一、问题的提出 1.设f(x)在x处连续,则有 f(x)≈f(x) [f(x)=f(x)+a] 2.设f(x)在x。处可导,则有 f(x)f(x)+f(xo)(x-xo) If(x)=f(x)+f(xo)(x-xo)+o(x-xo) 例如,当x很小时,e"≈1+x,n(1+x)≈x (如下图)
一、问题的提出 1.设 f (x)在x0处连续,则有 ( ) ( ) 0 f x f x [ f (x) = f (x0 ) + ] 2.设 f (x)在 0 x 处可导,则有 ( ) ( ) ( )( ) 0 x0 x x0 f x f x + f − [ ( ) ( ) ( )( ) ( )] 0 x0 x x0 o x x0 f x = f x + f − + − 例如, 当 x 很小时, e x x 1 + , ln(1 + x) x (如下图)
y=x 0.6 y=In(1+x) 0=1+x -0,5 0 0.5 02 0.4 0.6 0.8
x y = e y = 1+ x o x y = e o y = x y = ln(1 + x)

不足:1、精确度不高;2、误差不能估计。 问题:寻找函数P(x),使得f(x)≈P(x) 误差R(x)=f(x)-P(x)可估计 设函数f(x)在含有x,的开区间(a,b)内具有直到 (n+1)阶导数,P(x)为多项式函数 Pn(x)=4+41(x-x)+42(c-x)2+.+an(c-x)” 误差R.(x)=f(x)-Pn(x)
不足: 1、精确度不高; 2、误差不能估计。 问题: 寻找函数P(x),使得 f (x) P(x) 误差 R(x) = f (x) − P(x) 可估计 设函数 f ( x)在含有x0的开区间(a,b) 内具有直到 (n + 1)阶导数,P(x)为多项式函数 n n n P (x) a a (x x ) a (x x ) a (x x ) 0 2 = 0 + 1 − 0 + 2 − 0 ++ − 误差 R (x) f (x) P (x) n = − n
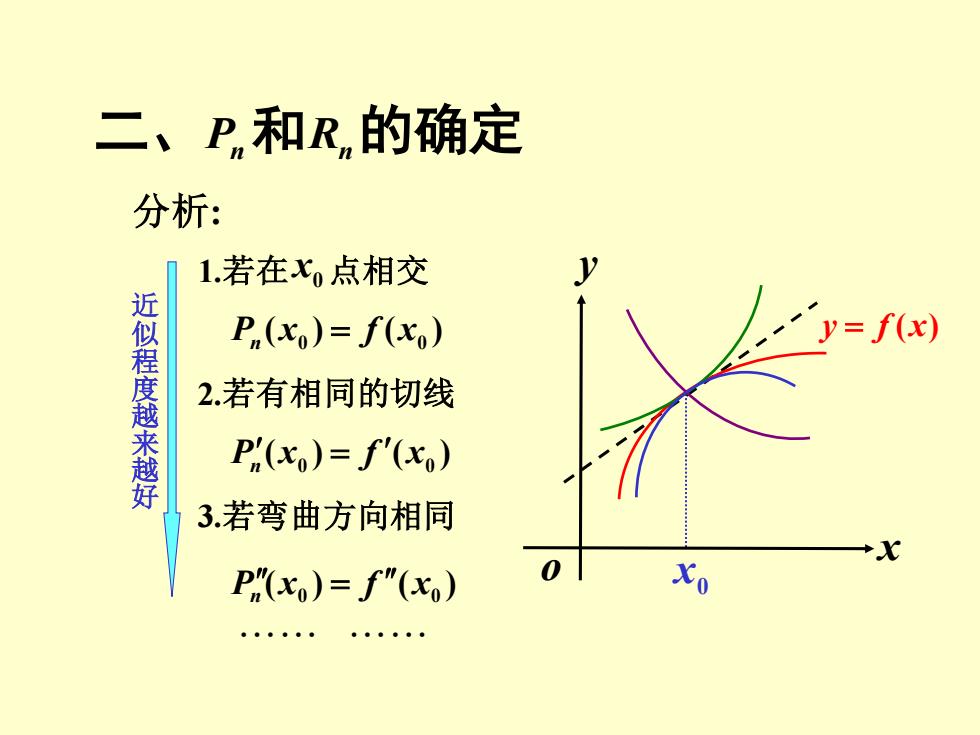
二、P和R的确定 分析: 1.若在x0点相交 近似程度越 P,(xo)=f(xo) =f(x) 2.若有相同的切线 越好 P"(xo)=f(xo) 3若弯曲方向相同 +x P"(x)=f"(x) xo
二、Pn和Rn的确定 0 x y = f (x) o x y 分析: ( ) ( ) 0 0 P x f x n = ( ) ( ) 0 0 P x f x n = ( ) ( ) 0 0 P x f x n = 2.若有相同的切线 3.若弯曲方向相同 近 似 程 度 越 来 越 好 1.若在 x0 点相交

假设P(x)=(K)k=1,2,n 。=f(x),1a,=f'(x),2a,=f"(x,) .,nan=fw(化) 得a=fx,)k=012, 代入Pn(x)中得 P()=+x-)+e-xP+ +((x-x)
假设 P x f x k n k k n ( ) ( ) 1,2, , 0 ( ) 0 ( ) = = ( ), 0 x0 a = f 代入P (x) n 中得 n n n x x n f x x x f x P x f x f x x x ( ) ! ( ) ( ) 2! ( ) ( ) ( ) ( )( ) 0 0 ( ) 2 0 0 0 0 0 + − − + = + − + 得 ( ) ( 0,1,2, , ) ! 1 0 ( ) f x k n k a k k = = 1 ( ), 1 0 a = f x 2! ( ) 2 x0 a = f , ! ( ) 0 ( ) n a f x n n =

三、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理如果函数f(x)在含有x,的 某个开区间(a,b)内具有直到(n+1)阶的导数,则当 x在(a,b)内时,f(x)可以表示为(x-x。)的一m 次多项式与一个余项R(x)之和: f)=f(x)+f(x)x-)+"-x) 21 +.+fm((x-x”+R,(x) n! 其中R(W=(x-七"专在x,与之间. (n+1):
三、泰勒(Taylor)中值定理 泰勒(Taylor)中值定理 如果函数f (x) 在含有x0的 某个开区间(a,b)内具有直到(n + 1)阶的导数,则当 x在(a,b)内 时, f (x) 可以表示为( ) x − x0 的一个n 次多项式与一个余项R (x) n 之和: ( ) ( ) ! ( ) ( ) 2! ( ) ( ) ( ) ( )( ) 0 0 ( ) 2 0 0 0 0 0 x x R x n f x x x f x f x f x f x x x n n n + + − + − = + − + 其中 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x ( 在x0与x 之间)

证明:由假设,Rn(x)在(a,b)内具有直到(n+1)阶 导数,且 Rn(x)=Pn(x)=P”(x)=.=R(xo)=0 两函数R(x)及(K-x)+1在以x及x为端点的 区间上满足柯西中值定理的条件,得 R(x)_R,(x)-R,(xo) (x-)1(-)-0 P(5) (5在x与x之间) (n+1)(51-xo)
由假设,R (x) n 在(a,b)内具有直到(n + 1)阶 导数,且 证明: 两函数R (x) n 及 1 0 ( ) + − n x x 在 以 0 x 及 x为端点的 区间上满足柯西中值定理的条件,得 ( ) ( 1)( ) ( ) 0 1 0 1 在x 与x之间 n x R n n + − = ( ) 0 ( ) ( ) ( ) ( ) 1 0 0 1 0 − − − = − + n+ n n n n x x R x R x x x R x ( ) ( ) ( ) ( 0 ) 0 ( ) R x0 = R x0 = R x0 = = R x = n n n n n

两函数R(x)及(n+1)(x-xo)"在以x,及51为端点 的区间上满足柯西中值定理的条件,得 P(5) E(51)-P(xo) (n+10(51-x)”(n+1)(5-x)”-0 P(52) (52在x与51之间) n(n+1)(52-x)-1 如此下去,经过(n+1)次后,得 R(x) _R+(5) (c-x)m= (n+1 (5在x与5m之间,也在x,与之间)
如此下去,经过(n + 1)次后,得 两函数R (x) n 及 n (n 1)(x x ) + − 0 在以 x0及 1为端点 的区间上满足柯西中值定理的条件,得 ( 1)( ) 0 ( ) ( ) ( 1)( ) ( ) 1 0 1 0 1 0 1 + − − − = + − n n n n n n x R R x n x R ( 1)! ( ) ( ) ( ) ( 1) 1 0 + = − + + n R x x R x n n n n (在x0与 n之 间,也在x0与x 之间) ( ) ( 1)( ) ( ) 1 2 0 1 2 0 2 在 与 之间 x n n x R n n − + − =

Pm(x)=0,.Rm(x)=f() 则由上式得 Rx=f"x-x(传在x,与之间) (n+1: k! 称为.f(x)按(x-x)的幂展开的n次近似多项式 元=含x-+R6四 称为f(x)按(x-x)的幂展开的n阶泰勒公式
= = − n k k k n x x k f x P x 0 0 0 ( ) ( ) ! ( ) ( ) 称为 f (x)按( ) x − x0 的幂展开的 n 次近似多项式 = = − + n k n k k x x R x k f x f x 0 0 0 ( ) ( ) ( ) ! ( ) ( ) 称为 f (x)按( ) x − x0 的幂展开的 n 阶泰勒公式 ( ) ( ) ( ) 1 ! ( ) ( ) 0 1 0 ( 1) x x 在x 与x之间 n f R x n n n + + − + = 则由上式得( ) 0, ( 1) = + P x n n ( ) ( ) ( 1) ( 1) R x f x n n n + + =