
初等丞数 一、基本初等函数 1.幂函数y=x“(μ是常数) y y=x y=√x (1,1
初等函数 一、基本初等函数 1.幂函数 = (是常数) y x o x y 2 y = x y = x y = x 1 1 (1,1) x y 1 =
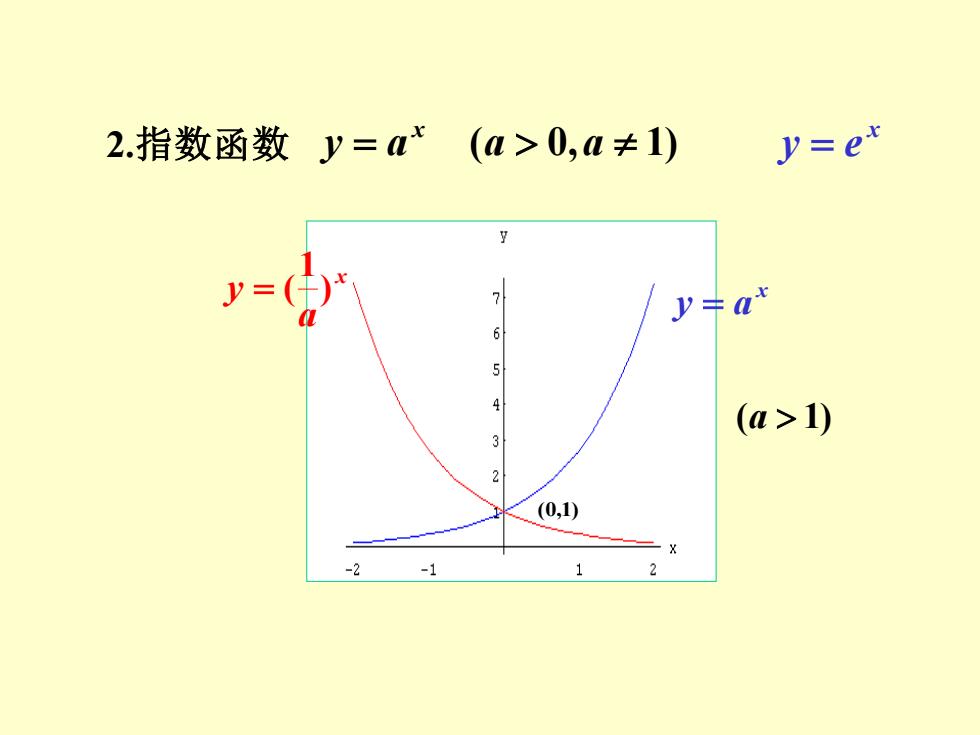
2.指数函数y=a(a>0,a≠1) y=ex y=()* ya 6 (a>1) (0,1) -v 2 -1
2.指数函数 y = a (a 0,a 1) x x y = e x y = a x a y ) 1 = ( (a 1) (0,1)
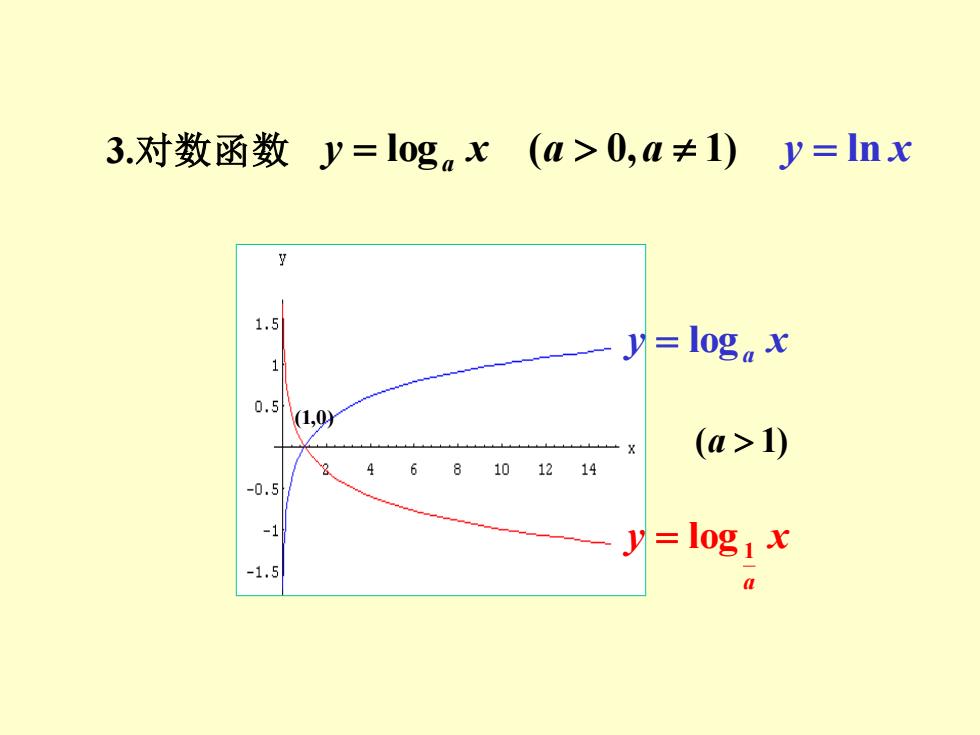
3.对数函数y=logx(a>0,a≠1)y=lnx 1.5 y=loga x 1 0.5 (1,0 (a>1) 468101214 -0.5 y =10g1X -1.5
3.对数函数 y = log x (a 0,a 1) a y = ln x y = loga x y x a 1 = log(a 1) (1,0)
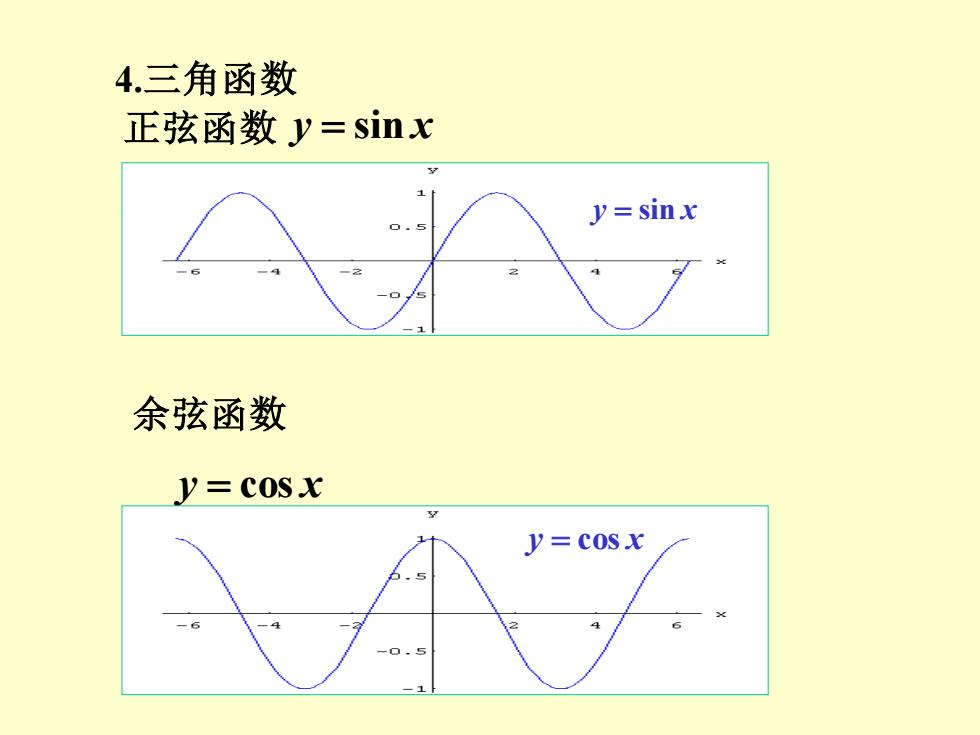
4.三角函数 正弦函数y=sinx y=sinx 余弦函数 y=COSx y=cosx
4.三角函数 正弦函数 y = sin x y = sin x 余弦函数 y = cos x y = cos x
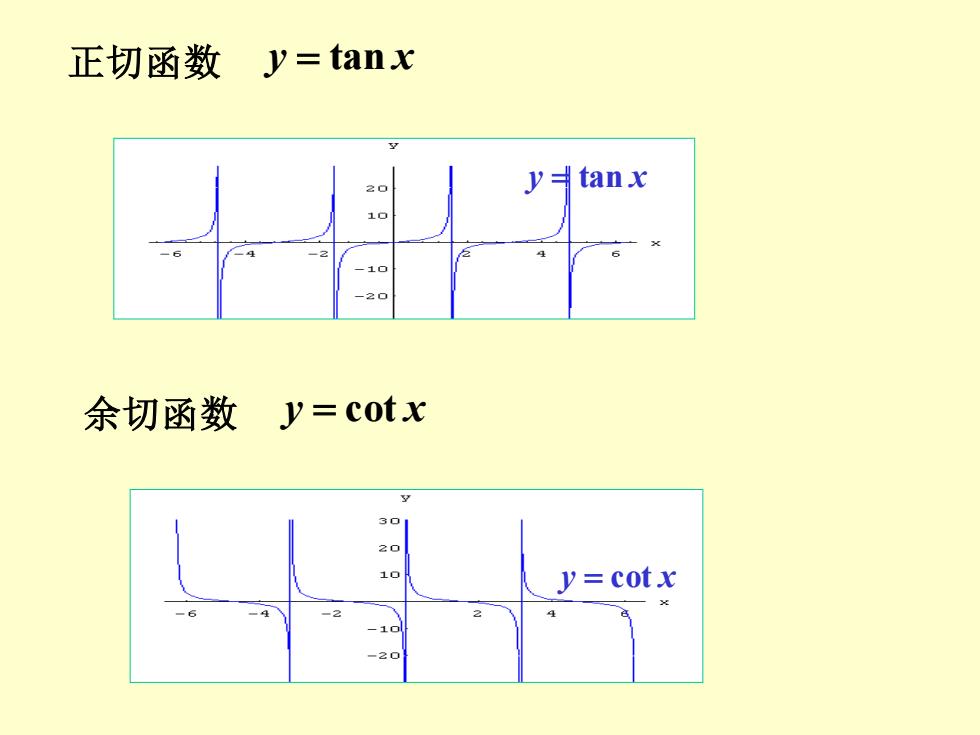
正切函数y=tanx 20 ytanx 10 -6 -2 -20 余切函数y=cotx 30 20 10 y=cotx 4
正切函数 y = tan x y = tan x 余切函数 y = cot x y = cot x
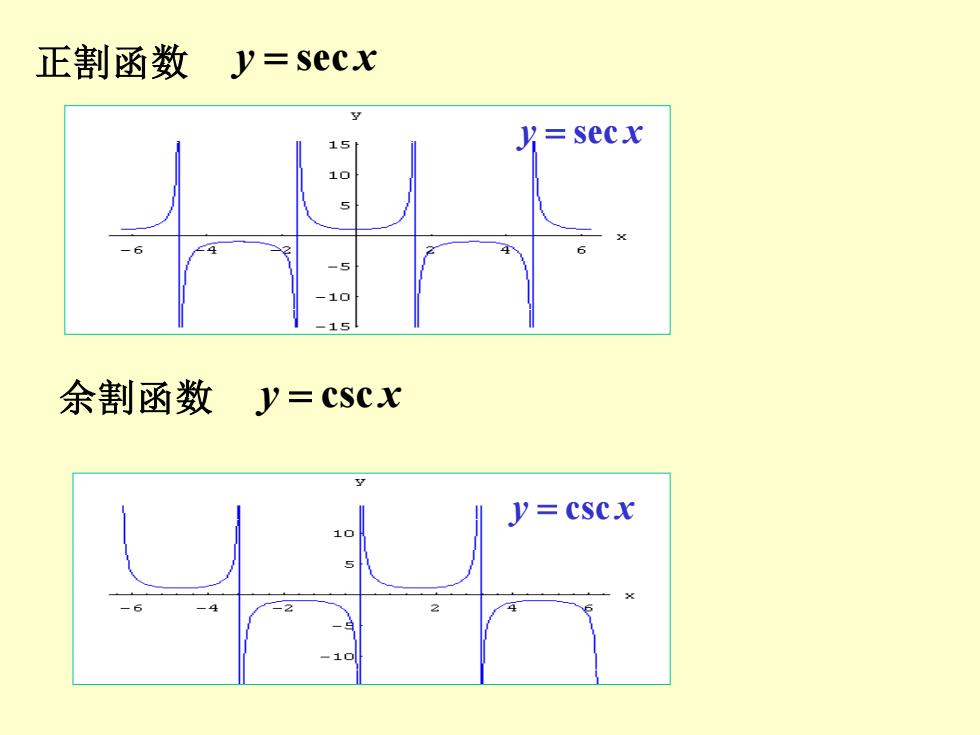
正割函数y=secx 15 y=secx 10 10 余割函数y=CsCx y=cscx 1口 10
正割函数 y = sec x y = sec x 余割函数 y = csc x y = csc x
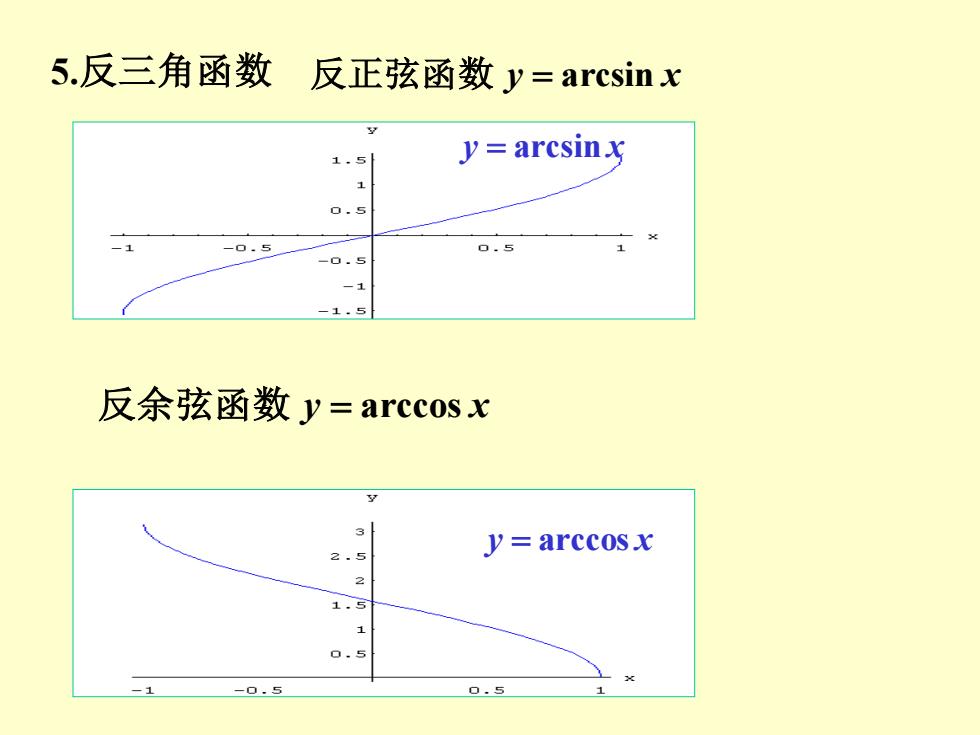
5.反三角函数 反正弦函数y=arcsinx 1.5 y=arcsinx 1 0.s -0.5 0.5 -0.5 -1 1.5 反余弦函数y=arccosx y=arccosx 2.5 2 1.5 1 0.5 一1 -0.5 0.5
5.反三角函数 反正弦函数 y = arcsin x y = arcsin x 反余弦函数 y = arccos x y = arccos x
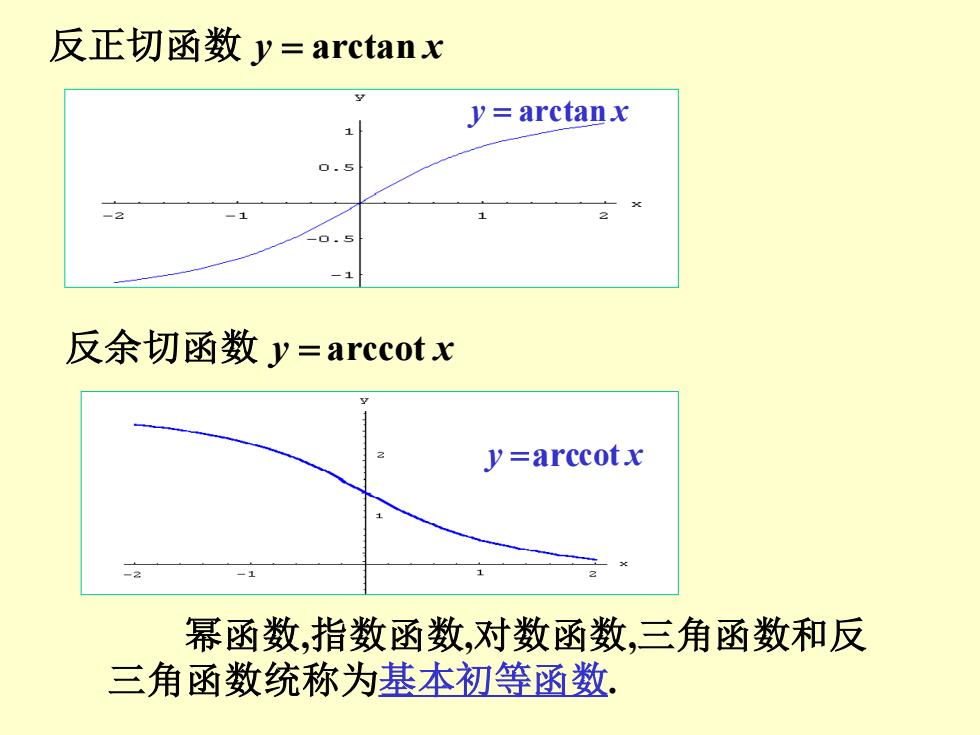
反正切函数y=arctanx y=arctanx 0.5 反余切函数y=arccotx y=arccotx 幂函数,指数函数,对数函数,三角函数和反 三角函数统称为基本初等函数
反正切函数 y = arctan x y = arctan x 反余切函数 y = arccot x y =arccot x 幂函数,指数函数,对数函数,三角函数和反 三角函数统称为基本初等函数

二、复合函数初等函数 1.复合函数 在实标问题中,有很多比较复杂的函数是由几个 比较简单的函数“叠置”而成的,如在简谐振动中 位移y与时间t的函数关系 y sin(at+p) 就是由三角函数y=sinw和线性函数u=ot+p “叠置”而成的, 设y=u,h=1-x2,→y=√1-x2
二、复合函数 初等函数 1.复合函数 在实际问题中,有很多比较复杂的函数是由几个 比较 简单的函数“叠置”而成的,如在简谐振动中 位移y与时间 t 的函数关系 y = sin(t +) 就是由三角函数 y = sin u 和线性函数 u = t + “叠置”而成的, 设 y = u, 1 , 2 u = − x 2 y = 1 − x

定义: 设函数y=f(W)的定义域Dr,而函数 u=p(x)的值域为Z。,若Dr∩Z。≠②,则称 函数y=fIp(x)川为x的复合函数, x←自变量,u←中间变量,y←因变量, 注意:1不是任何两个函数都可以复合成一个复 合函数的; Z。∩D,≠⑦—复合条件 例如y=arcsinu,.u=2+x2;y≠arcsin(2+x2)
定义: 设函数 y = f (u)的定义域Df , 而函数 u = (x)的值域为Z , 若 Df Z , 则 称 函 数 y = f[(x)]为x的复合函数. x 自变量, u 中间变量, y 因变量, 注意: 1.不是任何两个函数都可以复合成一个复 合函数的; Z Df ——复合条件 例如 y = arcsinu, 2 ; 2 u = + x arcsin(2 ) 2 y + x