
所属学院:经济管理与法学院 课程编号:21030207 课程名弥·轻这数学 学时/学分:48学时2学分 先修课程:无 适用专业:经济类专业 一、概述 (一)课程性质 数学是反映客观世界的科学,是对客观世界定性把握和定量描述,进而逐渐抽象概括形成方法和理 论,并且进行广泛应用的科学。数学是抽象的,又是具体的,是一种工具,也是一种文化,更是一种信 息。随着时代的发展,文明的进步,特别是二十世纪中叶以来,数学自身发生了巨大的变化,使得数学在 研究领域、研究方式和应用范围等方面得到了空前的发展。数学可以帮助人们更好地探求客观世界的规 律,并对现代社会中大量繁杂的信息作出最优的判断和选择,同时为人们交流信息提供了一种有效而简捷 的手段。数学作为一种普遍适用的技术,有助于人们收集、整理、描述信息、建立模型,进而解决问题 直接为社会创造价值。 经济数学课程是高职高专经济管理类专业学生的必修课的一门专业基础课,也是一门工具课,是在现 代科学技术、经济管理、人文科学中应用最广泛的一门课程。通过本课程的学习,使学生从思想观念到思 维方法上完成从初等数学到变量数学的转变,为今后学习后续课程 —其它专业基础课以及相关的专业课 程打下必要的数学基础,提供必需的数学概念、理论、方法、运算技能和分析问题解决问题的能力素质。 在经济数学的教学中必须遵循以应用为目的,以必需、够用为度的原则,注重理论联系实际,强调对学 生基本运算能力和分析问题、解决问题能力的培养,以努力提高学生的数学修养和素质。 (二)课程基本理念与设计思路 以适应社会需要为目标,以培养综合素质为主线设计学生的知识、能力、素质结构和培养方案,遵 循以应用为目的,以必需、够用为度"的教学原则。学生应了解或理解经济数学中函数、极限和连续、 一元函数微分学、一元函数积分学的基本概念与基本理论;强调掌握重要的基本概念、基本运算,注重知 识的应用。使学生掌握必要的数学基础知识及常用的数学方法:应注意各部分知识的结构及知识的内在联 系;培养学生运用所学知识分析问题、解决问题的能力;培养学生应用数学知识建立数学模型的能力(应 提倡的能力);培养学生的数学素养、创新意识、创新精神和自学能力 1、以能力培养为切入点,充分体现课程的基础性、应用性和发展性 数学是人们生活、劳动和学习必不可少的工具,能够帮助人们处理数据,进行计算、推理和证明,它 为其它学科提供了语言、思想和方法,从而数学的基础性地位无可替代,更不能偏废。经济数学教学在作 为专业基础课的同时,应充分遵循"学有所用、学有所需"的原则,而在教学过程中,都要从能力培养出 发,发掘学生的潜在的创新思维,以切实提高学生的综合素质。 2、以学生为中心,充分发挥学生的学习能动性 经济数学的学习内容应当根据实际的需求进行调整,而内容的呈现也应采用不同的表达方式,以满足 多样化的学习需求,同时教学活动心须建立在学生的接受能力基础之上。而教师也不是被动的,应调动 切可行的手段,激发学生的学习积极性,向学生提供充分从事数学活动的机会,帮助他们在自主探索和合 作交流的过程中真正理解和掌握数学知识与技能、数学思想和方法,获得广泛的数学活动经验,为学习和 实践提供有效的知识工具和良好的思维素质。 3、构建本课程新的评价体系,考察学生的输出"能力
所属学院:经济管理与法学院 课程编号:21030207 课程名称:经济数学 学时/学分:48学时/2学分 先修课程:无 适用专业:经济类专业 一、概述 (一)课程性质 数学是反映客观世界的科学,是对客观世界定性把握和定量描述,进而逐渐抽象概括形成方法和理 论,并且进行广泛应用的科学。数学是抽象的,又是具体的,是一种工具,也是一种文化,更是一种信 息。随着时代的发展,文明的进步,特别是二十世纪中叶以来,数学自身发生了巨大的变化,使得数学在 研究领域、研究方式和应用范围等方面得到了空前的发展。数学可以帮助人们更好地探求客观世界的规 律,并对现代社会中大量繁杂的信息作出最优的判断和选择,同时为人们交流信息提供了一种有效而简捷 的手段。数学作为一种普遍适用的技术,有助于人们收集、整理、描述信息、建立模型,进而解决问题, 直接为社会创造价值。 经济数学课程是高职高专经济管理类专业学生的必修课的一门专业基础课,也是一门工具课,是在现 代科学技术、经济管理、人文科学中应用最广泛的一门课程。通过本课程的学习,使学生从思想观念到思 维方法上完成从初等数学到变量数学的转变,为今后学习后续课程——其它专业基础课以及相关的专业课 程打下必要的数学基础,提供必需的数学概念、理论、方法、运算技能和分析问题解决问题的能力素质。 在经济数学的教学中必须遵循"以应用为目的,以必需、够用为度"的原则,注重理论联系实际,强调对学 生基本运算能力和分析问题、解决问题能力的培养,以努力提高学生的数学修养和素质。 (二)课程基本理念与设计思路 以适应社会需要为目标,以培养综合素质为主线设计学生的知识、能力、素质结构和培养方案, 遵 循"以应用为目的,以必需、够用为度"的教学原则。学生应了解或理解"经济数学"中函数、极限和连续、 一元函数微分学、一元函数积分学的基本概念与基本理论;强调掌握重要的基本概念、基本运算,注重知 识的应用。使学生掌握必要的数学基础知识及常用的数学方法;应注意各部分知识的结构及知识的内在联 系;培养学生运用所学知识分析问题、解决问题的能力;培养学生应用数学知识建立数学模型的能力(应 提倡的能力);培养学生的数学素养、创新意识、创新精神和自学能力。 1、以能力培养为切入点,充分体现课程的基础性、应用性和发展性 数学是人们生活、劳动和学习必不可少的工具,能够帮助人们处理数据,进行计算、推理和证明,它 为其它学科提供了语言、思想和方法,从而数学的基础性地位无可替代,更不能偏废。经济数学教学在作 为专业基础课的同时,应充分遵循"学有所用、学有所需"的原则,而在教学过程中,都要从能力培养出 发,发掘学生的潜在的创新思维,以切实提高学生的综合素质。 2、以学生为中心,充分发挥学生的学习能动性 经济数学的学习内容应当根据实际的需求进行调整,而内容的呈现也应采用不同的表达方式,以满足 多样化的学习需求,同时教学活动必须建立在学生的接受能力基础之上。而教师也不是被动的,应调动一 切可行的手段,激发学生的学习积极性,向学生提供充分从事数学活动的机会,帮助他们在自主探索和合 作交流的过程中真正理解和掌握数学知识与技能、数学思想和方法,获得广泛的数学活动经验,为学习和 实践提供有效的知识工具和良好的思维素质。 3、构建本课程新的评价体系,考察学生的"输出"能力
评价的主要目的是为了全面了解学生的数学学习历程,考察学生的实际能力,同时激励学生的学习和 改进教师的教学。但以往的评价手段过于单一,不能全面反映学生的真实情况,而且评价的价值取向犹为 偏颇。所以应建立评价目标多元、评价方法多样的评价体系。对数学学习的评价要关注学生学习的结果 也要关注学习的过程;要关注数学知识的掌握,也要关注数学知识的运用。总之,评价的结果优劣要经得 起实践检验。 二、课程目标 (一)总目标 本课程的总目标是要通过少对经济数学在高等教育阶段的学习,使学生能够获得相关专业课学习心须的 数学基础,适应未来深入学习、工作及进一步发展所必需的重要的数学知识,以及基本的数学思想方法和 必要的应用技能:使学生学会用数学的思维方式去观察、分析现实社会,去解决学习、生活、工作中遇到 的实际问题,从而进一步增进对数学的理解和兴趣:使学生具有一定的创新精神和提出问题分析问题解决 问题的能力,从而促进生活、事业的全面充分的发展;使学生既具有独立思考同时又具有团体协作精神 在科学工作事业中实事求是、坚持真理,勇于攻克难题。 (二)分目标: 1、知识目标:极限与连续, 一数微分学 、一元函数积分学、专业应用方面的基础知识、数学建模的 初步知识。 1)理解极限的概念,掌握极限的运算法则,能够熟练计算一般函数间极限。 2)理解微分的概念,掌握微分的运算法则,能够熟练计算一般函数的微分 3)理解积分的概念,掌握积分的运算法则,能够熟练计算一般函数的积分。 2、能力目标:逻辑推理能力、基本运算能力、自学能力、数学建模的初步能力、应用数学知识解决实际 问题的能力。 1)通过对极限概念的学习,使学生建立无限的思想观,并使学生能用"分割求和取极限"的思想方法求一些 诸如无穷数列和、图形面积等问题。 2)通过对微分的学习,使学生能够建立实际问题的模型,理解诸如最值方面的问题,并能分析、推证、 解释跟最值有关的一些现实现象 3)通过对积分的学习,使学生能够利用"微元法的思想方法,解决一些诸如求面积等问题, 4)通过对本课程的学习,使学生在掌握必要的基础知识的同时,具有一定的数学建模思想,并将这种思 想贯穿于整个提出问题分析问题解快问题的过程 5)通过对本课程的学习,使学生具有一定的自学能力和将数学思想扩展到其它领域的能力。 3、情感与态度:树垃辩证唯物主义世界观、培养学生良好的学习习惯、坚强的意志品格、严谨思维、求 实的作风。递深索.敢干创新的思想意识和良的团闭那队合作结神。 三 课程内容与要求 教学 应达到的知识技能 重点 单元 难点 内容 态度目标要求 时 1第一 7. (1)理解函数的概念: (1)基本初等函数。 (1)反函数的概念。 音 1函数 函数的定义,函数的表 (2)函数的单调性和奇 (2)数列极限的概念理 函数 (1) 示法,分段函数 偶性 解无穷小量和无穷大 的 函数的 (2)掌握函数的性质; (3)数列极限的概念 量:无穷小量与无穷大 极限 概念。 单调性,奇偶性,有界 理解无穷小量和无穷大 量的定义,无穷小量与 和 (2) 性,周期性。 景:无穷小景与无穷大 无穷大量的关系,无穷 连续函数的 量的定义,无穷小量与 小量与无穷大量的性
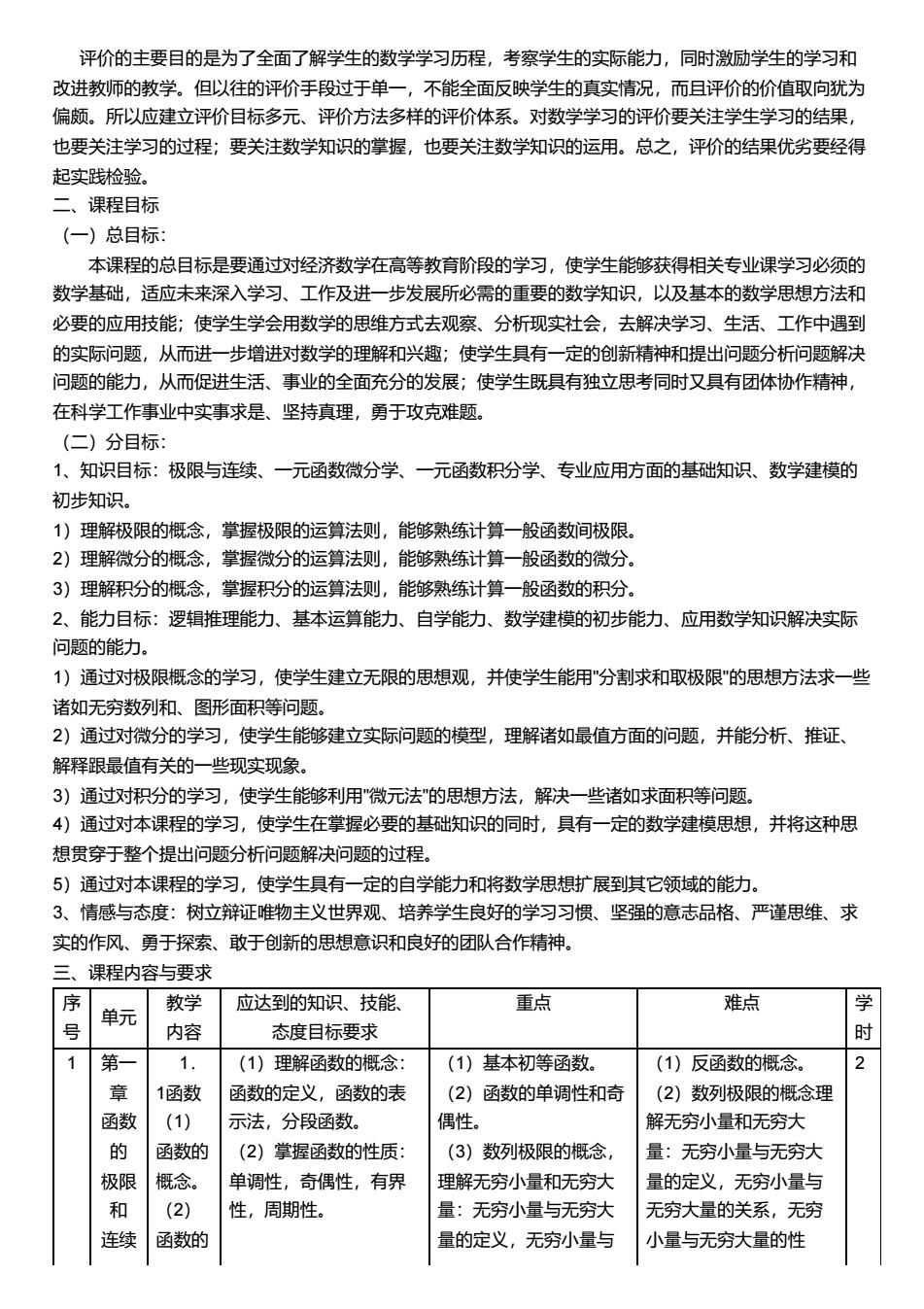
评价的主要目的是为了全面了解学生的数学学习历程,考察学生的实际能力,同时激励学生的学习和 改进教师的教学。但以往的评价手段过于单一,不能全面反映学生的真实情况,而且评价的价值取向犹为 偏颇。所以应建立评价目标多元、评价方法多样的评价体系。对数学学习的评价要关注学生学习的结果, 也要关注学习的过程;要关注数学知识的掌握,也要关注数学知识的运用。总之,评价的结果优劣要经得 起实践检验。 二、课程目标 (一)总目标: 本课程的总目标是要通过对经济数学在高等教育阶段的学习,使学生能够获得相关专业课学习必须的 数学基础,适应未来深入学习、工作及进一步发展所必需的重要的数学知识,以及基本的数学思想方法和 必要的应用技能;使学生学会用数学的思维方式去观察、分析现实社会,去解决学习、生活、工作中遇到 的实际问题,从而进一步增进对数学的理解和兴趣;使学生具有一定的创新精神和提出问题分析问题解决 问题的能力,从而促进生活、事业的全面充分的发展;使学生既具有独立思考同时又具有团体协作精神, 在科学工作事业中实事求是、坚持真理,勇于攻克难题。 (二)分目标: 1、知识目标:极限与连续、一元函数微分学、一元函数积分学、专业应用方面的基础知识、数学建模的 初步知识。 1)理解极限的概念,掌握极限的运算法则,能够熟练计算一般函数间极限。 2)理解微分的概念,掌握微分的运算法则,能够熟练计算一般函数的微分。 3)理解积分的概念,掌握积分的运算法则,能够熟练计算一般函数的积分。 2、能力目标:逻辑推理能力、基本运算能力、自学能力、数学建模的初步能力、应用数学知识解决实际 问题的能力。 1)通过对极限概念的学习,使学生建立无限的思想观,并使学生能用"分割求和取极限"的思想方法求一些 诸如无穷数列和、图形面积等问题。 2)通过对微分的学习,使学生能够建立实际问题的模型,理解诸如最值方面的问题,并能分析、推证、 解释跟最值有关的一些现实现象。 3)通过对积分的学习,使学生能够利用"微元法"的思想方法,解决一些诸如求面积等问题。 4)通过对本课程的学习,使学生在掌握必要的基础知识的同时,具有一定的数学建模思想,并将这种思 想贯穿于整个提出问题分析问题解决问题的过程。 5)通过对本课程的学习,使学生具有一定的自学能力和将数学思想扩展到其它领域的能力。 3、情感与态度:树立辩证唯物主义世界观、培养学生良好的学习习惯、坚强的意志品格、严谨思维、求 实的作风、勇于探索、敢于创新的思想意识和良好的团队合作精神。 三、课程内容与要求 序 号 单元 教学 内容 应达到的知识、技能、 态度目标要求 重点 难点 学 时 1 第一 章 函数 的 极限 和 连续 1. 1函数 (1) 函数的 概念。 (2) 函数的 (1)理解函数的概念: 函数的定义,函数的表 示法,分段函数。 (2)掌握函数的性质: 单调性,奇偶性,有界 性,周期性。 (1)基本初等函数。 (2)函数的单调性和奇 偶性。 (3)数列极限的概念, 理解无穷小量和无穷大 量:无穷小量与无穷大 量的定义,无穷小量与 (1)反函数的概念。 (2)数列极限的概念理 解无穷小量和无穷大 量:无穷小量与无穷大 量的定义,无穷小量与 无穷大量的关系,无穷 小量与无穷大量的性 2
性质。 (3)了解反函数:反函无穷大量的关系,无穷 质,两个无穷小量阶的 数的定义,反函数的图 小量与无穷大量的性 比较。 反函 质,两个无穷小量阶的 (3)利用两个重要极 数。 比较。 求极限的方法。 1.1函 (4)利用两个重要极限 数 求极限的方法。 (4 (4)理解复合函数的概 复合函 数的概 念,掌握复合函数的复 合与分解。 (5)了解基本初等函 (5) 数:幂函数,指数函 基本初 等函 数、对数函数、三角函 数 数、反三角函数。 6) (6)了解初等函数的概 初等函 念。 数的概 1.2极 (1)数列极限的概念: 数列,数列极限的定 (1) 义,能根据极限概念分 数列极 析函数的变化趋势. 限的概 (2)数列极限的性质: 唯一性,有界性,四则 (2) 运算定理,单调有界数 数列极 列,极限存在定理,掌 限的性 樱极限的四云筒法 质。 则. 1.2极 限 (3)理解函数极限的概 (3) 念:函数在一点处极限 函数极 的定义,左、右极限及 限的概 其与极限的关系,x趋于 念 无穷(X→0,×→+0, 4 (4) ×→∞)时函数的极限 2 函数在 (4)会求函数在一点处 一点处 的左极限与右极限,了 的左极 解函数在一点处极限存 限与右 在的充分必要条件。 极限
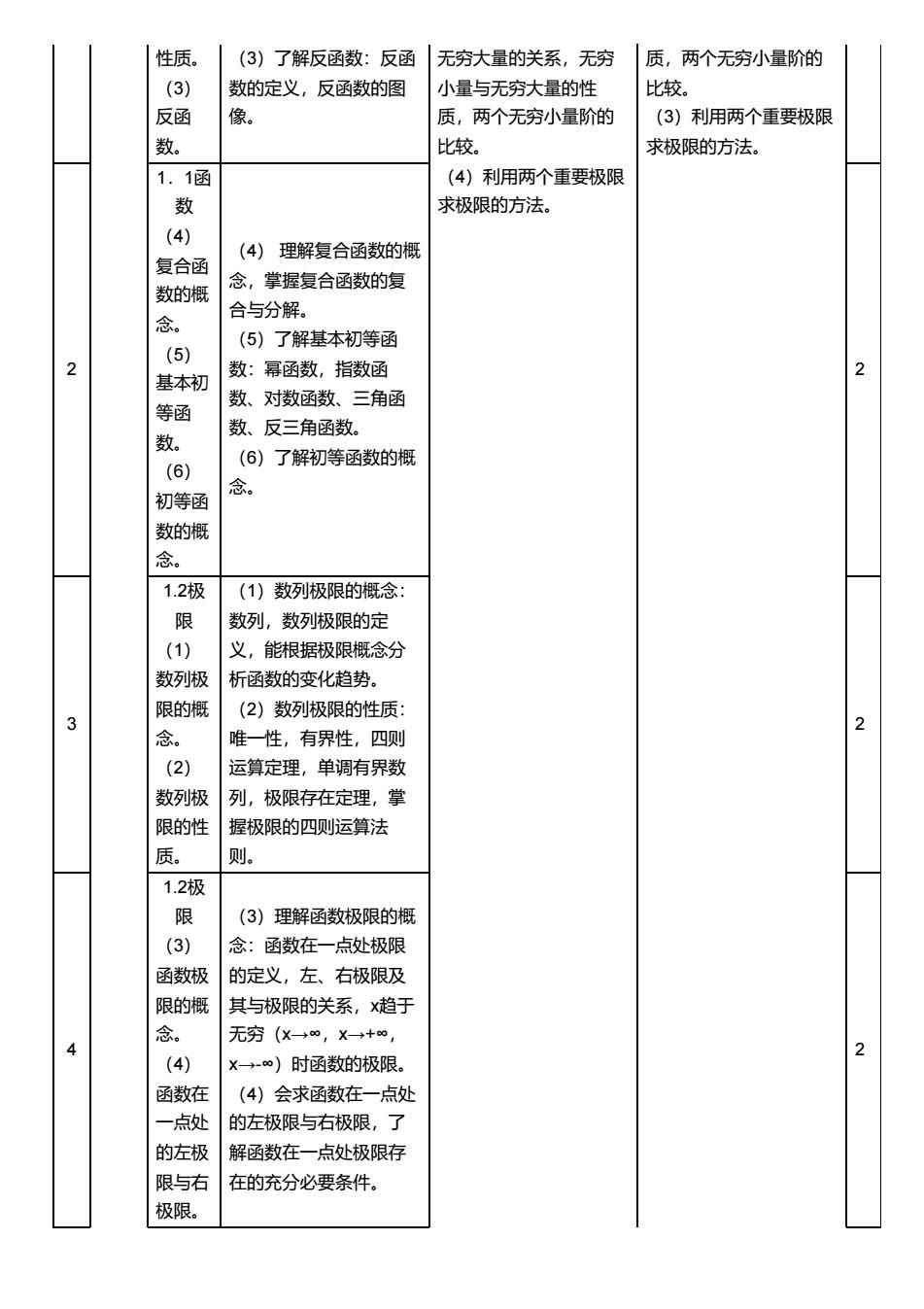
性质。 (3) 反函 数。 (3)了解反函数:反函 数的定义,反函数的图 像。 无穷大量的关系,无穷 小量与无穷大量的性 质,两个无穷小量阶的 比较。 (4)利用两个重要极限 求极限的方法。 质,两个无穷小量阶的 比较。 (3)利用两个重要极限 求极限的方法。 2 1.1函 数 (4) 复合函 数的概 念。 (5) 基本初 等函 数。 (6) 初等函 数的概 念。 (4) 理解复合函数的概 念,掌握复合函数的复 合与分解。 (5)了解基本初等函 数:幂函数,指数函 数、对数函数、三角函 数、反三角函数。 (6)了解初等函数的概 念。 2 3 1.2极 限 (1) 数列极 限的概 念。 (2) 数列极 限的性 质。 (1)数列极限的概念: 数列,数列极限的定 义,能根据极限概念分 析函数的变化趋势。 (2)数列极限的性质: 唯一性,有界性,四则 运算定理,单调有界数 列,极限存在定理,掌 握极限的四则运算法 则。 2 4 1.2极 限 (3) 函数极 限的概 念。 (4) 函数在 一点处 的左极 限与右 极限。 (3)理解函数极限的概 念:函数在一点处极限 的定义,左、右极限及 其与极限的关系,x趋于 无穷(x→∞,x→+∞, x→-∞)时函数的极限。 (4)会求函数在一点处 的左极限与右极限,了 解函数在一点处极限存 在的充分必要条件。 2
1.3极 限的运 算 (1) 极限的 四则运 (1)掌握极限的四则运 算法则。 算法 则 (2)熟练掌握用两个重 要极限求极限的方法。 用两个 重要极 限求极 限。 1.4无 穷小量 与无穷 大量 (1)理解无穷小、无穷 (1) 大的概念;无穷小量与 无穷 无穷大量的关系,无穷 6 2 小无 小量与无穷大量的性 穷大的 质,两个无穷小量阶的 概念 比较 关系 性质 比较 7 1.5函 (1)理解函数连续的概 2 数 念:函数在一点连续的 的定义,左连续和右连 续,函数在一点连续的 续 充分必要条件,函数的 性间断点及其分类。 (1) (2)掌握函数在一点处 函数连 连续的性质:连续函数 续的概的四则运算,复合函数 念。 的连续性,会求函数的 (2) 间断点及确定其类型。 函数在 (3)掌握闭区间上连续 点处 函数的性质:有界性定 连续的 理,最大值和最小值定 性质。 理,介值定理(包括零 点定理),会运用介值
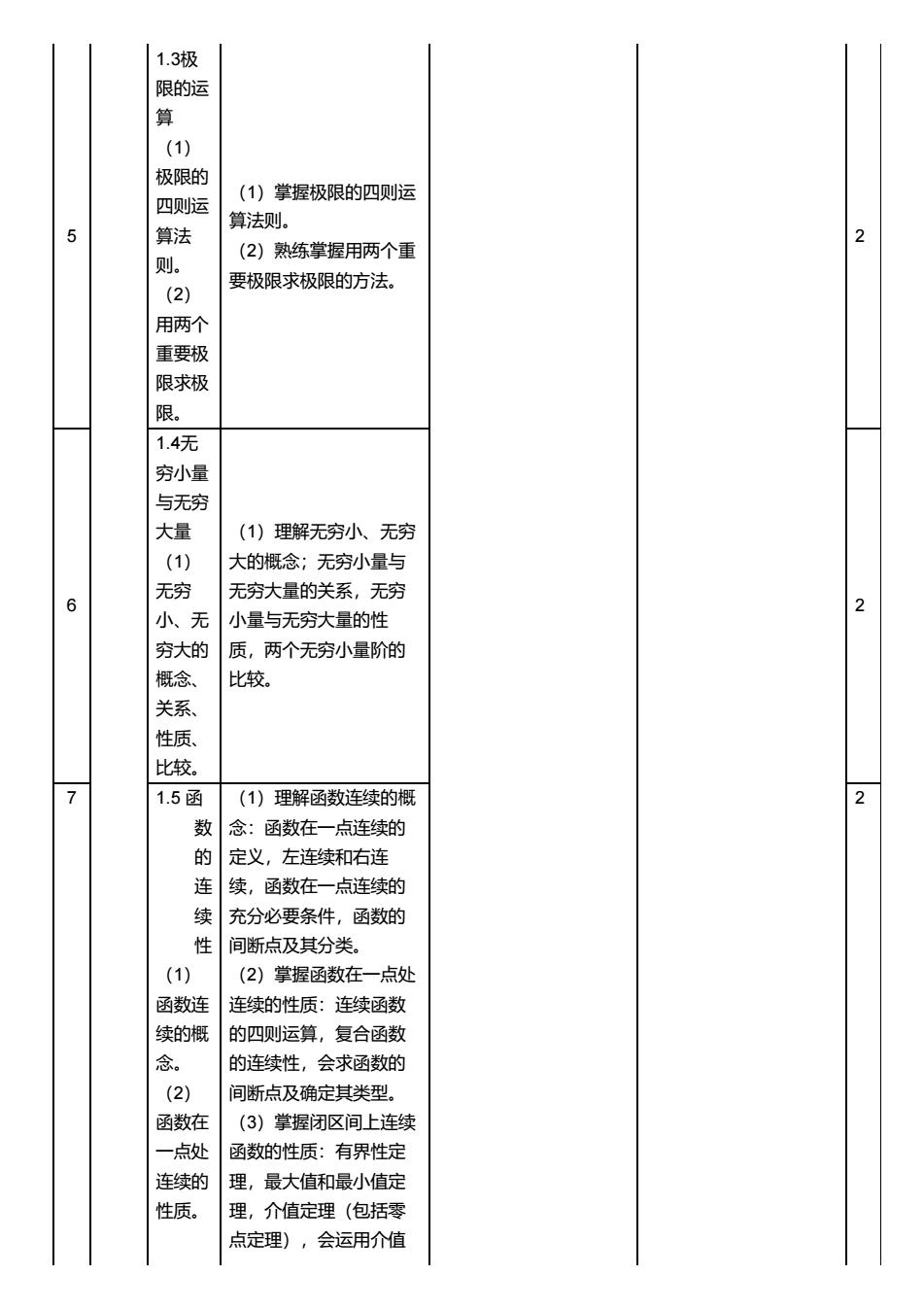
5 1.3 极 限的运 算(1) 极限的 四则运 算法 则。(2 ) 用两个 重要极 限求极 限。 ( 1)掌握极限的四则运 算法则。 (2)熟练掌握用两个重 要极限求极限的方法。 2 6 1.4 无 穷小量 与无穷 大量(1) 无穷 小、无 穷大的 概念、 关系、 性质、 比较。 ( 1)理解无穷小、无穷 大的概念;无穷小量与 无穷大量的关系,无穷 小量与无穷大量的性 质,两个无穷小量阶的 比较。 2 7 1.5 函数的连续性 ( 1 ) 函数连 续的概 念。(2 ) 函数在 一点处 连续的 性质。 ( 1)理解函数连续的概 念:函数在一点连续的 定义,左连续和右连 续,函数在一点连续的 充分必要条件,函数的 间断点及其分类。 (2)掌握函数在一点处 连续的性质:连续函数 的四则运算,复合函数 的连续性,会求函数的 间断点及确定其类型。 (3)掌握闭区间上连续 函数的性质:有界性定 理,最大值和最小值定 理,介值定理(包括零 点定理),会运用介值 2
(3) 定理推证一些简单命 闭区间 题。 上连续 (4)理解初等函数在其 函数的 定义区间上连续,并会 性质。 利用连续性求极限。 (4) 初等涵 数在其 定义区 间上连 续。 第二 (1)导数的概念及其几 (1)函数的微分概念。 2.1导 何意义,可导性与连续 (2)反函数的概念 导数 数的概 (1)理解导数的概念及 性的关系,用定义求函 (3)可导性与连续性的关 和 其几何意义,了解可导 数在一点处的导数。 微分 (1)导 性与连续性的关系,会 (2)曲线上一点处的切 (4)复合函数的求导方 数的概 用定义求函数在一点处 线方程与法线方程。 法,隐函数的求导方 念及其 的导数。 (3)复合函数的求导片 8 法、对数求导法以及由 2 几何意 (2)会求曲线上一点处 法,隐函数的求导方 参数方程所确定的函数 义 的切线方程与法线方 法、对数求导法以及由 的求导方法以及分段函 程 参数方程所确定的函数 数的求导 (2)导 (3)熟练掌握导数的基 的求导方法以及分段函 数的基 本公式。 数的求导。 本公 2.2导 数的运 算 (1) 导数的 (1)熟练掌握导数的四 四则运 则运算法则以及复合函 算。 数的求导方法. (2) 复合函 数的求 导 10 (2)掌握隐函数的求导 2.2导 法、对数求导法以及由 数的运 参数方程所确定的函数 算
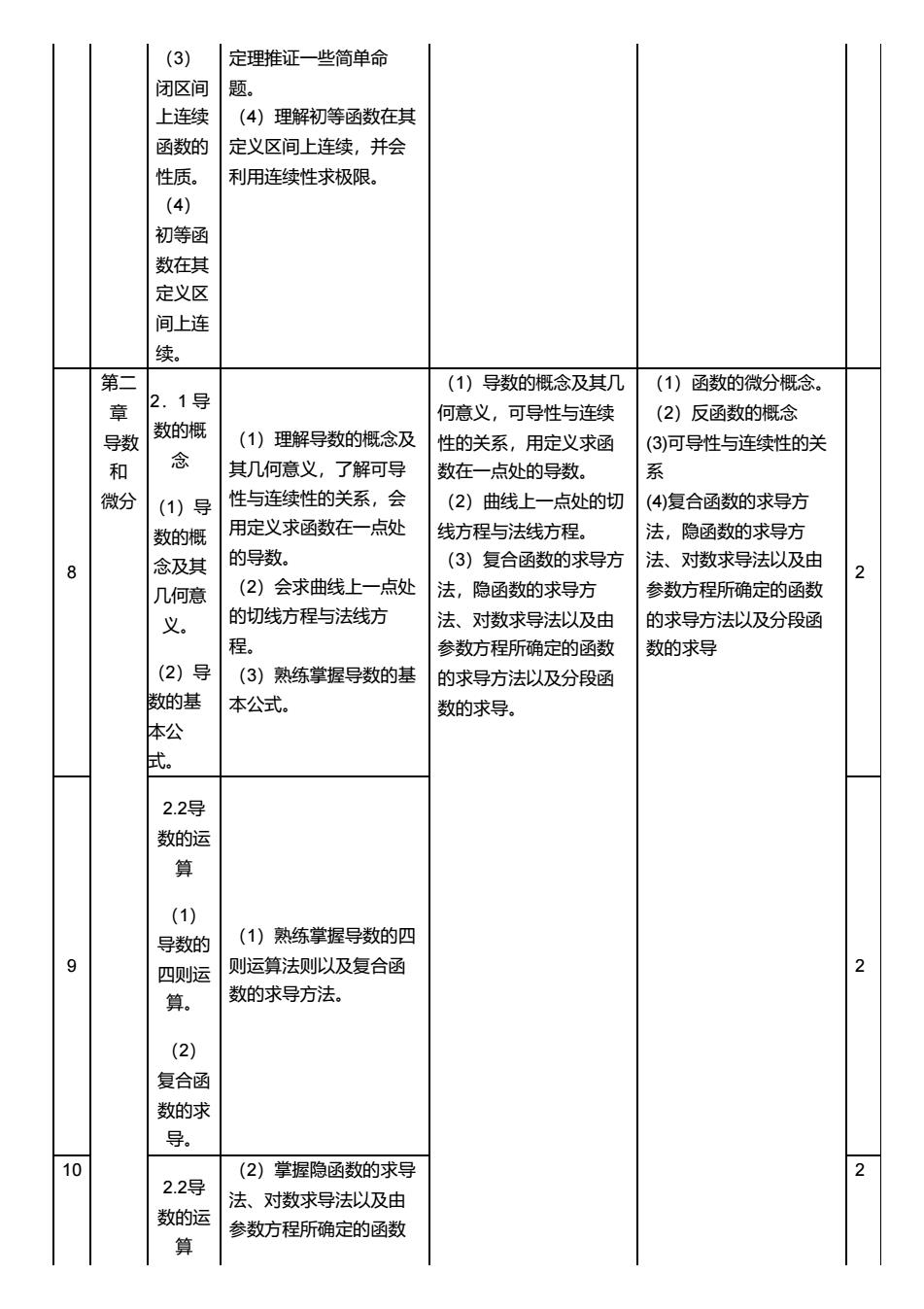
(3) 闭区间 上连续 函数的 性质。 (4) 初等函 数在其 定义区 间上连 续。 定理推证一些简单命 题。 (4)理解初等函数在其 定义区间上连续,并会 利用连续性求极限。 8 第二 章 导数 和 微分 2.1 导 数的概 念 (1)导 数的概 念及其 几何意 义。 (2)导 数的基 本公 式。 (1)理解导数的概念及 其几何意义,了解可导 性与连续性的关系,会 用定义求函数在一点处 的导数。 (2)会求曲线上一点处 的切线方程与法线方 程。 (3)熟练掌握导数的基 本公式。 (1)导数的概念及其几 何意义,可导性与连续 性的关系,用定义求函 数在一点处的导数。 (2)曲线上一点处的切 线方程与法线方程。 (3)复合函数的求导方 法,隐函数的求导方 法、对数求导法以及由 参数方程所确定的函数 的求导方法以及分段函 数的求导。 (1)函数的微分概念。 (2)反函数的概念 (3)可导性与连续性的关 系 (4)复合函数的求导方 法,隐函数的求导方 法、对数求导法以及由 参数方程所确定的函数 的求导方法以及分段函 数的求导 2 9 2.2导 数的运 算 (1) 导数的 四则运 算。 (2) 复合函 数的求 导。 (1)熟练掌握导数的四 则运算法则以及复合函 数的求导方法。 2 10 2.2导 数的运 算 (2)掌握隐函数的求导 法、对数求导法以及由 参数方程所确定的函数 2
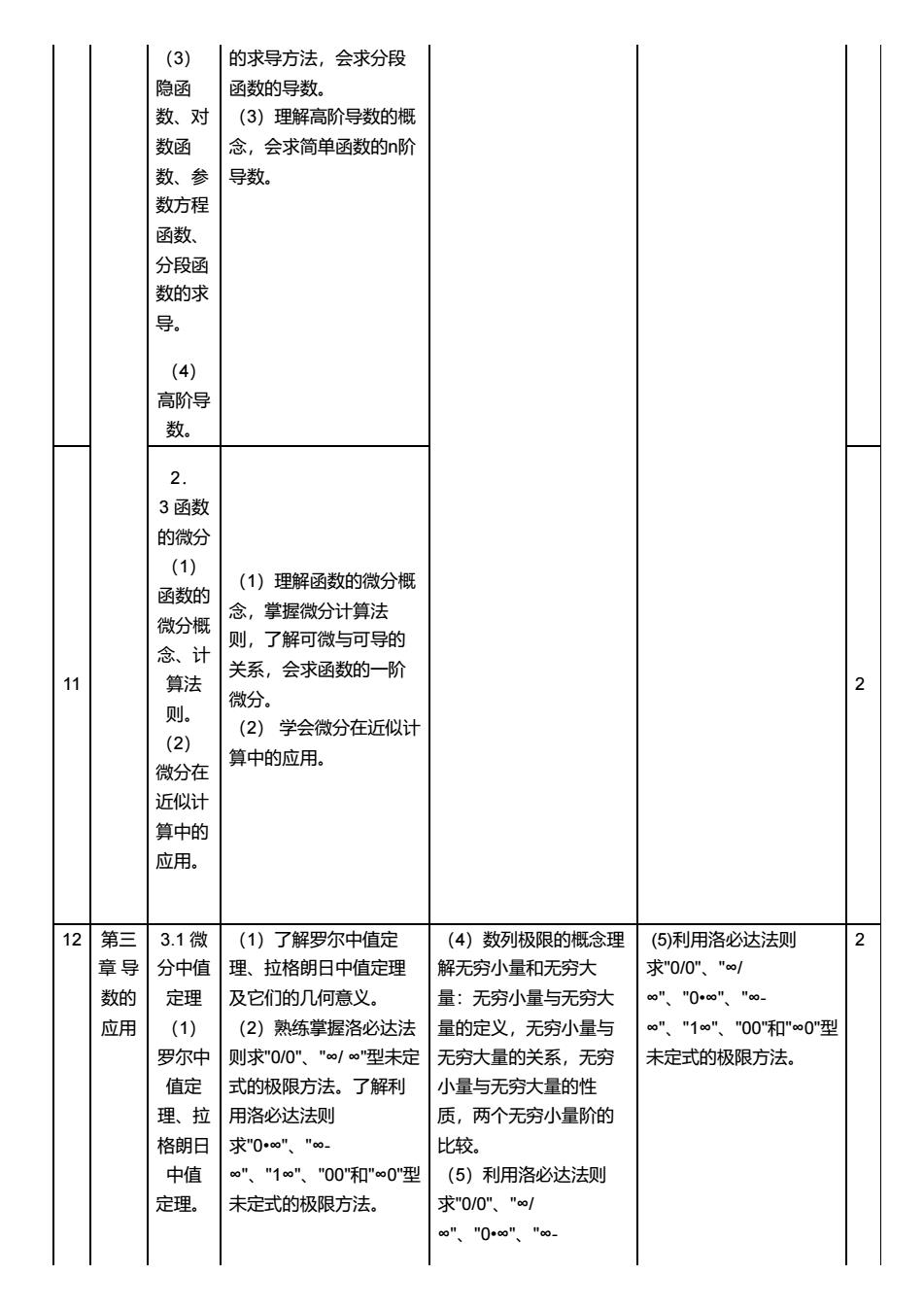
3 的求导方法,会求分段 隐函 函数的导数。 数、对 (3)理解高阶导数的概 数函 念,会求简单函数的n阶 数、 导数。 数方程 函数 分段函 数的求 导 (4) 高阶导 数。 2. 3函数 的微分 (1) (1)理解函数的微分概 函数的 微分概 念,掌握微分计算法 念、计 则, 了解可微与可导的 11 关系,会求函数的一阶 算法 2 微分。 则 (2)学会微分在近似计 (2) 算中的应用。 微分在 近似计 算中的 应用 12 第三3.1微 (1)了解罗尔中值定 (4)数列极限的概念理 (⑤)利用洛必达法则 2 章导分中值 理、拉格朗日中值定理 解无穷小量和无穷大 求"0/0"、"∞/ 数的 定理 及它们的几何意义. 量:无穷小量与无穷大 ∞"、0∞”、” 应用 (1) (2)熟练掌握洛必达法 量的定义,无穷小量与 、"1”"00和”0"型 罗尔中 则求"0/0""∞/∞"型未定 无穷大量的关系,无穷 未定式的极限方法。 值定 式的极限方法。了解利 小量与无穷大量的性 理、拉 用洛必达法则 质,两个无穷小量阶的 格朗日 求"0∞"、"∞- 比较。 中值 四”、"1∞”、"00"和"0"型 (5)利用洛必达法则 定理。 未定式的极限方法。 求"0/0、" co"、"0∞"、"eo-
(3) 隐函 数、对 数函 数、参 数方程 函数、 分段函 数的求 导。 (4) 高阶导 数。 的求导方法,会求分段 函数的导数。 (3)理解高阶导数的概 念,会求简单函数的n阶 导数。 11 2. 3 函数 的微分 (1) 函数的 微分概 念、计 算法 则。 (2) 微分在 近似计 算中的 应用。 (1)理解函数的微分概 念,掌握微分计算法 则,了解可微与可导的 关系,会求函数的一阶 微分。 (2) 学会微分在近似计 算中的应用。 2 12 第三 章 导 数的 应用 3.1 微 分中值 定理 (1) 罗尔中 值定 理、拉 格朗日 中值 定理。 (1)了解罗尔中值定 理、拉格朗日中值定理 及它们的几何意义。 (2)熟练掌握洛必达法 则求"0/0"、"∞/ ∞"型未定 式的极限方法。了解利 用洛必达法则 求"0•∞"、"∞- ∞"、"1∞"、"00"和"∞0"型 未定式的极限方法。 (4)数列极限的概念理 解无穷小量和无穷大 量:无穷小量与无穷大 量的定义,无穷小量与 无穷大量的关系,无穷 小量与无穷大量的性 质,两个无穷小量阶的 比较。 (5)利用洛必达法则 求"0/0"、"∞/ ∞"、"0•∞"、"∞- (5)利用洛必达法则 求"0/0"、"∞/ ∞"、"0•∞"、"∞- ∞"、"1∞"、"00"和"∞0"型 未定式的极限方法。 2

3.2洛 ∞”、"1∞”、"00和"∞0"型 必达法 未定式的极限方法。 (6)利用导数判定函数 的单调性及求函数的单 洛必达 调增、减区间的方法, 法则求 会利用函数的增减性证 极限。 明简单的不等式。 (7)函数极值的概念, 3.3函 函数的极值和最大 数的极 (小)值,求解简单的 (1)掌握利用导数判定 值 函数的单调性及求函数 应用问题。 (1) (8)判定曲线的凹凸 判定函 的单调增、减区间的方 性,会求曲线的拐点。 法,会利用函数的增减 数的单 (6)求曲线的水平渐近 调性。 性证明简单的不等式。 线与垂直渐沂线 (2) (2)理解函数极值的概 念,掌握求函数的极值 求函数 的极值 和最大(小)值的方 法,并且会解简单的应 和最大 用问题。 (小) 值。 3.4曲 线的凹 凸性及 拐点 (1) 曲线的 (1)会判定曲线的凹凸 凹凸 性,会求曲线的拐点。 14 性。 (2)会求曲线的水平渐 2 3 近线与垂直渐近线。 曲线的 水平渐 近线与 垂直新 近线。 15第四4.1不 (1)理解原函数与不定 (1)原函数与不定积分 (1)原函数与不定积分 章 定积分 积分概念及其关系,掌 概念及其关系 概念及其关系。 的概念 握不定积分性质,了解 (2)不定积分第一换元 (2)不定积分的方法选 与性质 原函数存在定理。 法,掌握第二换元法 择(包括第一类换元积
3.2 洛 必达法 则 (1) 洛必达 法则求 极限。 ∞"、"1∞"、"00"和"∞0"型 未定式的极限方法。 (6)利用导数判定函数 的单调性及求函数的单 调增、减区间的方法, 会利用函数的增减性证 明简单的不等式。 (7)函数极值的概念, 函数的极值和最大 (小)值,求解简单的 应用问题。 (8)判定曲线的凹凸 性,会求曲线的拐点。 (6)求曲线的水平渐近 13 线与垂直渐近线。 3.3函 数的极 值 (1) 判定函 数的单 调性。 (2) 求函数 的极值 和最大 (小) 值。 (1)掌握利用导数判定 函数的单调性及求函数 的单调增、减区间的方 法,会利用函数的增减 性证明简单的不等式。 (2)理解函数极值的概 念,掌握求函数的极值 和最大(小)值的方 法,并且会解简单的应 用问题。 2 14 3.4曲 线的凹 凸性及 拐点 (1) 曲线的 凹凸 性。 (2) 曲线的 水平渐 近线与 垂直渐 近线。 (1)会判定曲线的凹凸 性,会求曲线的拐点。 (2)会求曲线的水平渐 近线与垂直渐近线。 2 15 第四 章 不定 积分 4.1不 定积分 的概念 与性质 (1)理解原函数与不定 积分概念及其关系,掌 握不定积分性质,了解 原函数存在定理。 (1)原函数与不定积分 概念及其关系 (2)不定积分第一换元 法,掌握第二换元法 (1)原函数与不定积分 概念及其关系。 (2)不定积分的方法选 择(包括第一类换元积 2
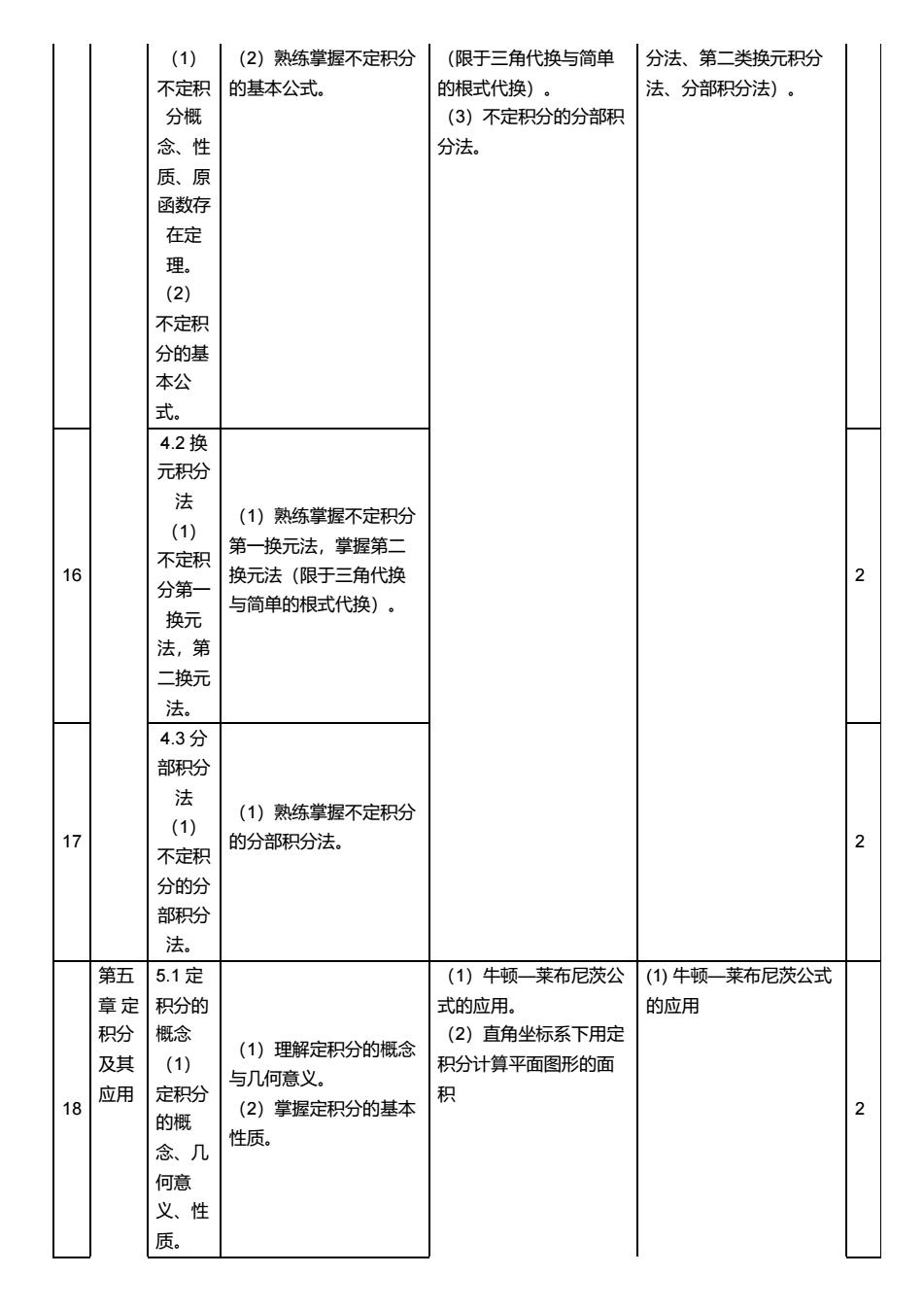
(1) (2)熟练掌握不定积分 (限于三角代换与简单 分法、第二类换元积分 不定积 的基本公式。 的根式代换)。 法、分部积分法)。 分概 (3)不定积分的分部积 分法 ⑧ 函数存 在定 理 (2) 不定积 分的基 本公 式。 4.2换 元积分 法 (1)熟练掌握不定积分 (1) 不定积 第一换元法,掌握第二 分第一 换元法(限于三角代换 换元 与简单的根式代换)。 法,第 二换元 法。 4.3分 部积分 法 (1)熟练掌握不定积分 1 (1) 不定积 的分部积分法。 分的分 部积分 法。 第五 5.1定 (1)牛顿一莱布尼茨公 (1)牛顿一莱布尼茨公式 章定 积分的 式的应用。 的应用 积分 概念 (2)直角坐标系下用定 及其 (1)理解定积分的概念 (1) 与几何意义。 积分计算平面图形的面 应用 18 定积分 (2)掌握定积分的基本 积 的概 性质。 念、几 何意 义、性 质
(1) 不定积 分概 念、性 质、原 函数存 在定 理。 (2) 不定积 分的基 本公 式。 (2)熟练掌握不定积分 的基本公式。 (限于三角代换与简单 的根式代换)。 (3)不定积分的分部积 分法。 分法、第二类换元积分 法、分部积分法)。 16 4.2 换 元积分 法 (1) 不定积 分第一 换元 法,第 二换元 法。 (1)熟练掌握不定积分 第一换元法,掌握第二 换元法(限于三角代换 与简单的根式代换)。 2 17 4.3 分 部积分 法 (1) 不定积 分的分 部积分 法。 (1)熟练掌握不定积分 的分部积分法。 2 18 第五 章 定 积分 及其 应用 5.1 定 积分的 概念 (1) 定积分 的概 念、几 何意 义、性 质。 (1)理解定积分的概念 与几何意义。 (2)掌握定积分的基本 性质。 (1)牛顿—莱布尼茨公 式的应用。 (2)直角坐标系下用定 积分计算平面图形的面 积 (1) 牛顿—莱布尼茨公式 的应用 2

5.2定 积分的 计算 (1) 变上限 (1)理解变上限的定积 分是变上限的函数,堂 定积 握变上限定积分求导数 求导 的方法。 数。 (2) (2)掌握牛顿一莱布尼 牛顿 茨公式。 莱布尼 茨公 式。 5.2定 积分的 计算 (3) 定积分 (3)掌握定积分的换元 积分法与分部积分法。 的换元 积分法 与分部 积分 法。 5.3定 (1)掌握直角坐标系下 积分的 用定积分计算平面图形 应用 的面积。 第六6.1经 1基本经济函数及对应的1基本经济函数及对应的 济学模 (1)学会利用数学的极 经济意义; 经济意义: 数学 限知识解决复利、抵押 2对经济函数进行边际 2对经济函数进行边际 模型 (1) 贷款问题: 弹性分析,并理解其经 弹性分析,并理解其经 复利、 济总义: 济总义: 抵押贷 款 (2) (2)了解基本经济函数 及对应的经济意义: 基本经 24 济函 数。 (3)学会利用导数知识 3 对经济函数进行边际、 (3) 弹性分析,并理解其经 经济函 济意义; 数的边
19 5.2定 积分的 计算 (1) 变上限 定积分 求导 数。 (2) 牛顿— 莱布尼 茨公 式。 (1)理解变上限的定积 分是变上限的函数,掌 握变上限定积分求导数 的方法。 (2)掌握牛顿—莱布尼 茨公式。 2 20 5.2定 积分的 计算 (3) 定积分 的换元 积分法 与分部 积分 法。 (3)掌握定积分的换元 积分法与分部积分法。 2 21 5.3定 积分的 应用 (1)掌握直角坐标系下 用定积分计算平面图形 的面积。 2 22 第六 章 数学 模型 6.1经 济学模 型 (1) 复利、 抵押贷 款。 (2) 基本经 济函 数。 (3) 经济函 数的边 (1)学会利用数学的极 限知识解决复利、抵押 贷款问题; 1 基本经济函数及对应的 经济意义; 2对经济函数进行边际、 弹性分析,并理解其经 济意义; 1 基本经济函数及对应的 经济意义; 2对经济函数进行边际、 弹性分析,并理解其经 济意义; 2 23 (2)了解基本经济函数 及对应的经济意义; 2 24 (3)学会利用导数知识 对经济函数进行边际、 弹性分析,并理解其经 济意义; 2

际、弹 性分 析 共计 48课时 四、实施建议 (一)教学建议 1实践环节要求:单设习题课,也可边讲边练。作业要每节必留,全部批改。 2本大纲及大纲说明书是根据高职高专数学指导委员会提出的对高职高专课程的基本要求制定的, (二)考核评价建议 对学习过程的评价与对学习结果的评价相统一的原则。既不仅要关注对学生学习结果的最后判断,更 要关注学习过程的发展、变化状态,随时把握它们的发展态势,使之不断得到调节和完善。 1过程性评价:每节上交作业,重点内容部分进行习题课并测试。 2终结性评价:期末考试闭卷考试。 总评成绩中平时作业占15%,平时测试占15%,闭卷考试占70%。 要求:部分试讲小论文,、讲稿Word文档及ppt文档于考查之日上交。 (三)教材选用与编写建议 《经济数学》杨丽肖丽媛主编内蒙古大学出版社 本教材为2010年自主开发教材 (四)实验实训设备配置建议:无 (五)课程资源开发与利用建议 1多媒体课件:已经有电子教案,课件正在开发】 2网络课程资料:建设期。 五、参考文献 1《经济数学》(同济大学等)同济大学数学系主编高等教育出版社 2《新编经济数学》上下册于铭钦编著陕西人民教育出版社 3《经济数学》(高职高专规划教材),侯风波主编高等教育出版社 4《应用数学》(高职高专规划教材),侯风波主编科学出版社 5《计算机数学基础》高等教育出版社刘树利主编 编写人:杨丽 审核人: 编写日期:2010年8月16日
际、弹 性分 析。 共计 48课时 四、实施建议 (一)教学建议 1 实践环节要求:单设习题课,也可边讲边练。作业要每节必留,全部批改。 2 本大纲及大纲说明书是根据高职高专数学指导委员会提出的对高职高专课程的基本要求制定的。 (二)考核评价建议 对学习过程的评价与对学习结果的评价相统一的原则。既不仅要关注对学生学习结果的最后判断,更 要关注学习过程的发展、变化状态,随时把握它们的发展态势,使之不断得到调节和完善。 1 过程性评价:每节上交作业,重点内容部分进行习题课并测试。 2 终结性评价:期末考试闭卷考试。 总评成绩中平时作业占15%,平时测试占15%,闭卷考试占70%。 要求:部分试讲小论文,、讲稿Word文档及ppt文档于考查之日上交。 (三)教材选用与编写建议 《经济数学》 杨丽 肖丽媛主编 内蒙古大学出版社 本教材为2010年自主开发教材 (四)实验实训设备配置建议:无 (五)课程资源开发与利用建议 1 多媒体课件:已经有电子教案,课件正在开发。 2 网络课程资料:建设期。 五、参考文献 1 《经济数学》(同济大学等) 同济大学数学系主编 高等教育出版社 2 《新编经济数学》上下册 于铭钦编著 陕西人民教育出版社 3 《经济数学》(高职高专规划教材),侯风波主编 高等教育出版社 4 《应用数学》(高职高专规划教材),侯风波主编 科学出版社 5 《计算机数学基础》 高等教育出版社 刘树利主编 编 写 人:杨丽 审 核 人: 编写日期:2010年8 月16 日