
1.写出下列复数的实部,虚部,模和幅角: (1)1+W3:(2)1-cosa+isina,0≤a<2π:(3)emx,x为实数:(4)e: 0d:6:):0哥o产:0em,p是实 的实函数。 we=1.m=5,Aa=c+m-2.Ag=02-号+2a (2)Re=1-cosa,Im=sina,Am=(1-cosa)'+sina=2-2cosa=2sin tan(Arg)-singr2sin cos =o所以Ag-+2r 2sin号 2 (3)Am=1,Arg=sinx+2kz,Re=cos(sinx),Im=sin(sinx): (4)z=x+y,e=e“,Am=ey,Arg=x+2kπ,Re=e'cosx,m=e'sinx (5)Am=e,Arg=y+2kπ,Re=e'cosy,Im=e'siny: o-e-e学,a=2外Aa=1.Ng2n+2, Re-ow im-sin )i=5em泸-5ef传-,m=0.wAm-5,Ag-g+m+2a Re2cosc Im-(sin m周-于学.子 Re=” (9)Am=e,Arg=l+2kπ,Re=ecos1,Im=esinl (10)Am=1,Arg=(x)+2kz,Re=cos[o(x)].Im=sin[o(x)]:
1.写出下列复数的实部,虚部,模和幅角: (1)1 3 + i ;(2)1 cos sin − + α i α ,0 2 ≤α < π ;(3) i x sin e , x 为实数;(4) iz e ; (5) z e ;(6) 4 −1;(7) 1+ i ;(8) 1 1 i i + − ;(9) 1 i e + ;(10) i x( ) e ϕ ,ϕ ( ) x 是实变数 x 的实函数。 (1)Re 1 = ,Im 3 = , 2 2 Am Re Im 2 = + = , Im Arg arctan 2 2 Re 3 k k π π π ⎛ ⎞ ⎜ ⎟ + =+ ⎝ ⎠ = ; (2)Re 1 cos = − α ,Im sin = α , ( )2 2 Am 1 cos sin 2 2cos 2sin 2 = α − + =− = αα α , ( ) 2 2sin cos sin 2 2 tan Arg cot 1 cos 2 2sin 2 α α α α α α == = − ,所以 Arg 2 2 = k π α π − + ; (3)Am 1 = , Arg sin 2 =xk + π , Re cos sin = ( x) ,Im sin sin = ( x) ; (4)z x iy = + , iz y ix e e− + = ,Am y e− = ,Arg 2 =x k + π ,Re cos y e x − = ,Im sin y e x − = ; (5)Am x = e , Arg 2 =y k + π , Re cos x = e y , Im sin x = e y ; (6) ( ) 1 2 1 4 2 4 4 1 n i i n e e π π π + + −= = ⎡ ⎤ ⎣ ⎦ ,( n = 0,1,2,3),Am 1 = , 2 1 Arg 2 4 n = k π π + + , 2 1 Re cos 4 n = π ⎛ ⎞ + ⎜ ⎟ ⎝ ⎠, 2 1 Im sin 4 n = π ⎛ ⎞ + ⎜ ⎟ ⎝ ⎠; (7) 2 2 4 4 4 8 12 2 i n in ie e π π π π ⎛ ⎞ ⎛⎞ ⎜ ⎟ ⎜⎟ + + ⎝ ⎠ ⎝⎠ += = ,( n = 0,1), 4 Am 2 = ,Arg 2 8 =n k π + + π π , ( ) 4 4 Re 2 cos 1 2 cos 8 8 n n π π π ⎛ ⎞ = + =− ⎜ ⎟ ⎝ ⎠ , ( ) 4 Im 1 2 sin 8 n π = − ; (8) ( ) 1 4 2 2 2 2 2 4 4 1 2 1 2 i n n i i n i i e e e i e π π π π π π π + + ⎛ ⎞ ⎜ ⎟ + ⎝ ⎠ − + ⎡ ⎤ = == ⎢ ⎥ − ⎣ ⎦ ,( n = 0,1),Am 1 = ,Arg 2 4 =n k π + + π π , ( ) 1 Re 2 n − = , ( ) 1 Im 2 n − = ; (9)Am = e , Arg 1 2 = + kπ , Re cos1 = e ,Im sin1 = e ; (10)Am 1 = , Arg 2 =x k ϕ ( ) + π , Re cos = ⎡ϕ ( x)⎤ ⎣ ⎦ , Im sin = ⎡ϕ ( x)⎤ ⎣ ⎦ ;

2.把下列关系用几何图形表示出来: ),1a-b:(9)+Rez0且y=0,即x0且y=51+x: rg(e+1-)=arg[x+1+i(y-l)]=5x+1=0且y-1>0
2.把下列关系用几何图形表示出来: (1) z 2 ;(2) 1 Re 2 z > ,1 Im 2 − ;(9) z z + Re 1 且 y = 0,即 x 且 y x = 3 1( + ) ; arg 1 arg 1 1 1 0 ( ) () 2 z i x iy x π +− = ++ − = ⇔ += ⎡ ⎤ ⎣ ⎦ 且 y −1 0 >
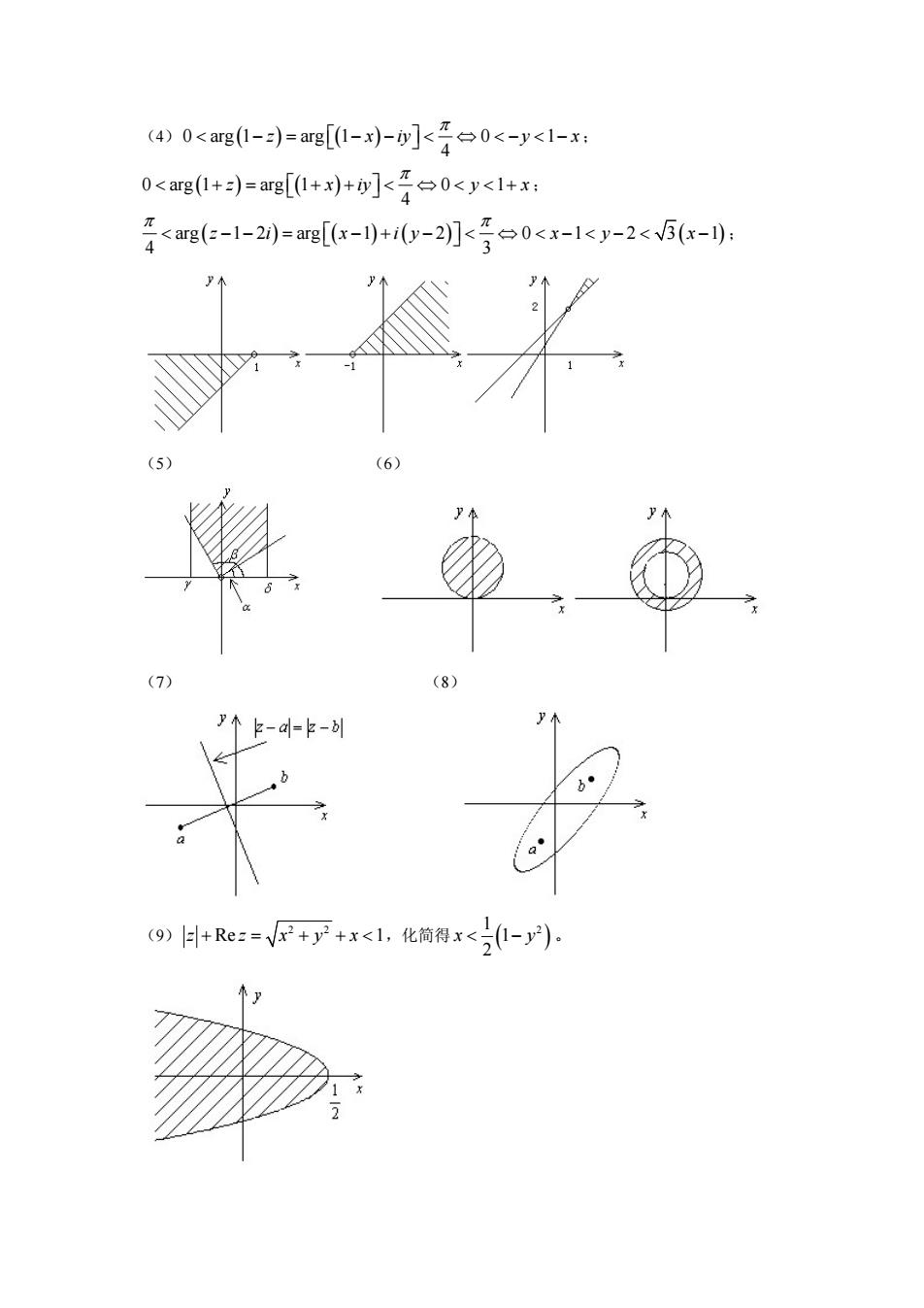
(4)0<arg-)=arg[-x-]<年台0<-y<l-x: 0<agl+)=arg[0+x+]<平台0<y<1+x: 牙<a8e-1-2)=ag[0x-+i0y-2]小<号台0<x-1<y-2<V5(x-): 5 (9)+Re:=V++x<1,化简得x<(1-y2)
(4)0 arg 1 arg 1 0 1 () () 4 z x iy y x π < − = − − < ⇔ <− < − ⎡ ⎤ ⎣ ⎦ ; 0 arg 1 arg 1 0 1 () () 4 z x iy y x π < + = + + < ⇔ < <+ ⎡ ⎤ ⎣ ⎦ ; arg 1 2 arg 1 2 0 1 2 3 1 ( ) ( )( ) ( ) 4 3 z i x iy x y x π π < −− = − + − < ⇔ < −< − < − ⎡ ⎤ ⎣ ⎦ ; (5) (6) (7) (8) (9) 2 2 z z xyx + = + +< Re 1,化简得 ( ) 1 2 1 2 x < − y

w计周所0 02。 3已陶-复数,面出,-,三,是上并指出它们之的儿何关系 把:写成pe”,则正=pe0+n,即把:逆时针旋转90度。-z=peo),即把:逆时到 装转0度。三=心,即:关于实箱的对称点。},即:关于华位圆的对称点· 41流证到医部1,a,6为任室复数 医-传阁谱
(10) ( ) ( ) ( ) 2 2 2 2 1 1 2 1 1 z i x y ix x iy z i x iy x y − + −− + − = = + ++ + + ,所以0 arg 4 z i z i ⎛ ⎞ − π 。 3.已知一复数 z ,画出iz , −z , z , 1 z , 1 z ,并指出它们之间的几何关系。 把 z 写成 i e ϕ ρ ,则 i( 2) iz e ϕ π ρ + = ,即把 z 逆时针旋转 90 度。 i( ) z e ϕ π ρ + − = ,即把 z 逆时针 旋转 180 度。 i z e ϕ ρ − = ,即 z 关于实轴的对称点。 1 1 i e z ϕ ρ = ,即 z 关于单位圆的对称点。 1 1 i e z ϕ ρ − = ,即 z 关于单位圆的对称点。 4.若 z =1,试证明 1 az b bz a + = + , a ,b 为任意复数。 ( )( ) ( )( ) 2 2 2 2 2 1 az b az b az b a abz abz b bz a bz a bz a b abz abz a + + + +++ == = + + + +++ ,所以 1 az b bz a + = +

5.证明下列各式: (1 -1s-1+arg: o补-产-即子 D先证5 记:=p, -1"2-2cs-2sin 2slol-larg=. -H*-s-后g (2) 国。与在得一圆周上、《=野等B=子,由于同所对周周角是 风6角价-卡所-,事ag浮-子 6.用复数:表示曲线上的变点。(I)写出经过点α且与复数b所代表的矢量平行的直线方 程:(2)写出以d和-d为焦点,长轴长2a的椭圆方程(a>d)。 (1)矢量:-a与矢量b平行,所以:-a=kb,k为实数: (2)由椭圆定义得-d+上+d=2a. 7.用复数运算法则推出:(1)平面直角坐标平移公式:(2)平面直角坐标旋转公式
5.证明下列各式: (1) z z zz −≤ −+ 1 1 arg ; (2)若 123 zz z = = ,则 3 2 2 31 1 1 arg arg 2 z z z zz z − = − 。 (1)先证 1 arg z z z − ≤ 。 记 i z e ϕ = ρ , 1 1 2 2cos 2 sin arg 2 z i e z z ϕ ϕ −= −= − = ≤ = ϕ ϕ 。 1 1 1 1 1 1 arg z z zz z zz z z z z z z z −= − + −≤ − + −= −+ −≤ −+ 。 (2) 如图, 1z , 2 z , 3 z 在同一圆周上, 3 2 3 1 arg z z z z α − = − , 2 1 arg z z β = 。由于同弧所对圆周角是 圆心角的一半,所以 1 2 α = β ,即 3 2 2 31 1 1 arg arg 2 z z z zz z − = − 。 6.用复数 z 表示曲线上的变点。(1)写出经过点 a 且与复数b 所代表的矢量平行的直线方 程;(2)写出以 d 和 −d 为焦点,长轴长 2a 的椭圆方程( a d > )。 (1)矢量 z a − 与矢量b 平行,所以 z a kb − = , k 为实数; (2)由椭圆定义得 zd zd a −++ = 2 。 7.用复数运算法则推出:(1)平面直角坐标平移公式;(2)平面直角坐标旋转公式

(1)设坐标系xOy的原点O在坐标系xOy中的坐标是(xo,)。P点在xOy系中的坐 标是(x,y),在x0y系中坐标(xy)。如上面左图,令O丽=:,0严=,O可=。 则=-0,即x+y=x-x。+i(0-为),由此得x=x-x,y=y- (2)将坐标系xOy绕原点逆时针旋转日角得到坐标系xOy。如上面右图,xOy系中 只是比xOy系中z的幅角小0,即'=ze,由此得x=xcose+ysin日 y'=-xsin+ycos0. 8.设复数,·与满足-三=二三.证明:5-53-5- 2-532-53 自∠小-2C同h国-a代-国=q-q.用 2-=-=-
(1)设坐标系 x′ ′′ O y 的原点O′ 在坐标系 xOy 中的坐标是( x0 0 , y ) 。 P 点在 xOy 系中的坐 标是( ) x, y ,在 x′ ′′ O y 系中坐标( ) x′, y′ 。如上面左图,令OP z = JJJG ,OP z ′ = ′ JJJG ,OO z0 ′ = JJJJG 。 则 0 z zz ′ = − ,即 x′ ′ + =− + − iy x x i y y 0 0 ( ) ,由此得 0 x′ = x x − , 0 y yy ′ = − 。 (2)将坐标系 xOy 绕原点逆时针旋转θ 角得到坐标系 x′O y′ ′ 。如上面右图,x′ ′′ O y 系中 z′ 只是比 xOy 系中 z 的幅角小θ ,即 i z ze− θ ′ = ,由此得 xx y ′ = cos sin θ + θ , yx y ′ =− + sin cos θ θ 。 8.设复数 1z , 2 z , 3 z 满足 2 1 1 3 31 23 z z z z zz zz − − = − − 。证明: 21 32 13 z z zz zz − =− =− 。 如图, 2 1 3 1 z z AB i A e z z AC − ∠ = − , 1 3 2 3 AC i C z z e z z BC − ∠ = − 。所以 AB AC AC BC = ,∠A = ∠C 。 由∠ =∠ A C 可得 AB BC = ,代入 AB AC AC BC = 可得 AB BC AC = = ,即 21 32 13 z z zz zz −=− =−

9.(1)给出1,2,3三点共线的充要条件:(2)给出,52,5,5,四点共圆的充要条件。 (1)若三点共线,则矢量一与矢量2-,平行,反之也成立。所以三点共线的充要条 件是二三=实数. 52-33 (2) 如图若四点共圆,则有∠ACB=∠ADB(同弧所对圆周角相等)。反之也成立。写成复数 形式即为三/三=实数。 23-23/22-24 10.求下列方程的根,并在复平面上画出它们的位置。 (1)2+1=0:(2)z3+8=0:(3)4-1=0:(4)+1=0:(5)2m+1=0,n为 正整数:(6)2+2:cos1+1=0,0<1<π。 (1)=i: (2):=2e号-2:3):=±1,: 4:e号e: (5):=er+2a2m,k=0,1.,2n-1: (6)=-e
9.(1)给出 123 zz z , , 三点共线的充要条件;(2)给出 1234 zz zz , 四点共圆的充要条件。 (1)若三点共线,则矢量 1 3 z z − 与矢量 2 3 z z − 平行,反之也成立。所以三点共线的充要条 件是 1 3 2 3 z z z z − = − 实数。 (2) 如图若四点共圆,则有 ∠ =∠ ACB ADB (同弧所对圆周角相等)。反之也成立。写成复数 形式即为 1 3 1 4 23 24 z z z z zz zz − − = − − 实数。 10.求下列方程的根,并在复平面上画出它们的位置。 (1) 2 z + =1 0 ;(2) 3 z + = 8 0 ;(3) 4 z −1 0 = ;(4) 4 z +1 0 = ;(5) 2 1 0 n z + = ,n 为 正整数;(6) 2 z z + += 2 cos 1 0 λ ,0 < λ < π 。 (1) z = ±i ; (2) 3 2 ,2 i z e π ± = − ; (3) z i = ± ± 1, ; (4) 3 4 4 , i i ze e π π ± ± = ; (5) i kn ( 2 2 ) z e π π + = , k n = − 0,1, ,2 1 " ; (6) i z e± λ = −

11.设:=p+ig是实系数方程a+a2+a,:2+.+anz”=0的根,证明三=p-ig也是此 方程的根。 对方程两边取共轭得a+a+a,之+.+a,"=0,即三也满足此方程。 12.证明:sinp=(cos40-4c0s2p+3). eo-4e2w+3=eo-l+41-e2m)=e2e(e2o-e2e)-4e(ee-ep) =2ie sin2-8ie sin=2i(cos2+isin2)sin2-8i(cos+isin)sin =8sin'+i(sin40-4sin2p) 取等式两边实部即得证。 13.把sinno和cos np用sinp和cosp表示出米。 cosp+isinnp=(eoso+ising)°=2.n )cos"osin' -星旷a0-两w一m0 n! 宫-a-wm n! 比较两边实部和虚部得: w-2凶-2opsm2o [-2] smp=宫x+-2=可c n!
11.设 z p iq = + 是实系数方程 2 01 2 0 n n a az a z a z + + ++ = " 的根,证明 z p iq = − 也是此 方程的根。 对方程两边取共轭得 2 01 2 0 n n a az a z a z + + ++ = " ,即 z 也满足此方程。 12.证明: ( ) 4 1 sin cos 4 4cos 2 3 8 ϕ ϕϕ = − + 。 ( ) ( ) ( ) 4 2 4 2 22 2 4 3 1 41 4 i i i i i i i ii i e e e e e e e ee e ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕϕ ϕ − − − + = −+ − = − − − ( ) ( ) 2 2 sin 2 8 sin 2 cos 2 sin 2 sin 2 8 cos sin sin i i ie ie i i i i ϕ ϕ = − = + −+ ϕ ϕ ϕ ϕ ϕ ϕ ϕϕ ( ) 4 =+ − 8sin sin 4 4sin 2 ϕ ϕϕ i 取等式两边实部即得证。 13.把sin nϕ 和cos nϕ 用sinϕ 和cosϕ 表示出来。 ( ) 0 ( ) ! cos sin cos sin cos sin ! ! n k n nk k k n i nin i knk ϕ ϕ ϕ ϕ ϕϕ − = + =+ = − ∑ ( ) ( )( ) [ / 2] 2 2 0 ! 1 cos sin 2! 2! n k nk k k n kn k ϕ ϕ − = = − − ∑ ( ) ( )( ) ( ) 1 /2 21 21 0 ! 1 cos sin 2 1! 2 1! n k nk k k n i k nk ϕ ϕ ⎡ ⎤ − ⎣ ⎦ −− + = + − + −− ∑ 比较两边实部和虚部得: ( ) ( )( ) [ / 2] 2 2 0 ! cos 1 cos sin 2! 2! n k nk k k n n kn k ϕ ϕ ϕ − = = − − ∑ ; ( ) ( )( ) ( ) 1 /2 21 21 0 ! sin 1 cos sin 2 1! 2 1! n k nk k k n n k nk ϕ ϕ ϕ ⎡ ⎤ − ⎣ ⎦ −− + = = − + −− ∑

14.将下列和式表示成有限形式:①)立c0sk知:(2)立sink如。 e贤e肾-e学) oeee I-omp el =l 1-eto ee-e号 sm号 比较两边实部和虚部得: 名oso inco sin29na+p 2—, ∑sinko n 记L2为方程=1的n个根,即=e台,k=L2.n-1。则有 ”-1=(e-0(-)(-)(2-), e-e-小nl 令上试两边:1则有1-宁. 1-六气e-2m好-2台m -)学5g-2-号.m告÷ 16.求下列序列{a}的聚点和极限,如果是实数序列,则同时求出上下极限。 wa=6少2eya=旷2aga=ntr+: ④a=2m1+ヅ:6)a-+}mg:66-+动mg
14.将下列和式表示成有限形式:(1) 1 cos n k kϕ = ∑ ;(2) 1 sin n k kϕ = ∑ 。 22 2 1 2 1 22 2 sin 1 2 1 sin 2 nn n ii i n in n i ik i i i ii i k ee e n e ee e e e ee e ϕϕ ϕ ϕ ϕ ϕϕ ϕ ϕ ϕϕ ϕ ϕ ϕ − + − = ⎛ ⎞ ⎜ ⎟ − − ⎝ ⎠ == = − ⎛ ⎞ ⎜ ⎟ − ⎝ ⎠ ∑ 比较两边实部和虚部得: ( ) 1 1 sin cos 2 2 cos sin 2 n k n n k ϕ ϕ ϕ = ϕ + ∑ = , ( ) 1 1 sin sin 2 2 sin sin 2 n k n n k ϕ ϕ ϕ = ϕ + ∑ = 。 15.证明: ( ) 1 2 1 sin sin sin 2n n n nn n π π π − − ⋅ ⋅⋅ = " 。 记 12 1 1, , , , n zz z " − 为方程 1 n z = 的 n 个根,即 2k i n k z e π = , k n =1,2, , 1 " − 。则有 1 1 ( )( 12 1 )( ) ( ) n n z z zz zz zz −= − − − − " − , 所以( )( ) ( ) 1 2 12 1 1 1 1 n n n n z zz zz zz z z z z − − − − − − − = = + + ++ − " " 。 令上式两边 z =1,则有 1 2 1 1 n k i n k e n π − = ⎛ ⎞ ⎜ ⎟ − = ⎝ ⎠ ∏ 。 2 2 1 2 sin 2 sin k kk k k k i ii i i i i n nn n n n k k e e e e ie e e n n ππ π π π π π ⎛ ⎞ − π − π − =− − =− = ⎜ ⎟ ⎝ ⎠ , 1 1 1 1 11 2 1 1 2 1 11 1 2 sin 2 sin n k n k n nn k i i i n n n n k kk k k ee n n n π π π π π − = − − −− − + − − = == ⎛ ⎞ ∑ ⎜ ⎟ −= = = ⎝ ⎠ ∏ ∏∏ ,即 1 1 1 sin 2 n n k k n n π − − = ∏ = 。 16.求下列序列{an} 的聚点和极限,如果是实数序列,则同时求出上下极限。 (1) ( ) 1 2 1 n n n a n = − + ;(2) ( ) 1 1 2 1 n n a n = − + ;(3) ( )( ) 121 n n an n i = +− + ; (4) 21 1 ( )n n a n ni = ++− ;(5) 1 sin 6 n i n a n ⎛ ⎞ π = + ⎜ ⎟ ⎝ ⎠ ;(6) 1 1 cos 2 3 n n a n ⎛ ⎞ π = + ⎜ ⎟ ⎝ ⎠

(1)聚点±12,极限无,上极限12,下极限-12: (2)聚点0,极限0,上下极限0: (5)聚点0,±12,±√52,±1,极限无: (6)聚点±1/2,土1,极限无,上极限1,下极限-1。 以.正明序列a=1+宁计号+分-nn极限存在 先证话h0+列sx,其中x20. 式右半部分得证,同样可证左半部分。 自安可得点+}号 a4=h+0.即a是送好 ()o.>In(+1)in(le(()-mm =2等9-ha=0 即an是递减有下界序列,所以极限存在。 1证明ee恒等式空-(②儿之小一可-。 右边-2f-后- -.Pbo F-l.fbo,F-Phw.Pw =∑f,f-∑fw,f+∑w四, =∑fmf+w可,=2∑” =公w-官=左边
(1)聚点± 1/2,极限无,上极限 1/2,下极限-1/2; (2)聚点 0,极限 0,上下极限 0; (3)聚点∞,极限∞; (4)聚点∞,极限∞; (5)聚点 0, ± 1/2,± 3 /2,± 1,极限无; (6)聚点± 1/2, ± 1,极限无,上极限 1,下极限-1。 17.证明序列 11 1 1 ln 2 3 n a n n =+ + + − " 极限存在。 先证 ln 1( ) 1 x x x x ≤ +≤ + ,其中 x ≥ 0 。 令 f () ( ) x xx = +− ln 1 ,则 ( ) 1 1 0 1 1 x f x x x ′ = − =− ≤ + + ,所以 fx f ( ) () ≤ = 0 0 ,不等 式右半部分得证,同样可证左半部分。 由此可得 1 11 ln 1 n nn 1 ⎛ ⎞ + ⎜ ⎟ ⎝ ⎠ 得 ( ) 11 1 ln 1 1 ln 1 ln 1 ln 1 ln 2 3 n a n n ⎛ ⎞⎛ ⎞ ⎛ ⎞ > ++ + + + + + + − ⎜ ⎟⎜ ⎟ ⎜ ⎟ ⎝ ⎠⎝ ⎠ ⎝ ⎠ " 34 1 1 ln 2 ln ln 1 0 2 3 n n n n ⎛ ⎞ ⎛⎞ + = ⋅⋅⋅ ⋅ − = + > ⎜ ⎟ ⎜⎟ ⎝ ⎠ ⎝⎠ " 即 n a 是递减有下界序列,所以极限存在。 18.证明 Lagrange 恒等式: 2 2 2 2 1 11 n nn kk k k k j jk k k k kj zw z w zw zw = == < ⎛ ⎞⎛ ⎞ = −− ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ ∑ ∑∑ ∑ 。 右边 ( )( ) 2 2 , k j k j jk k j jk kj k j z w zw zw zw zw < = −− − ∑ ∑ 22 2 2 22 , k j k j j k k j k j jk k k kj k j k j k j k j z w z w z w zzww zzww <<< < =−−+ + ∑∑∑∑∑ 2 2 2 2 , k j k j kjk j kj k j k j z w z w zzww ≠ ≠ =−+ ∑∑∑ 2 2 k k kjk j k k j j k kj k j z w zzww zw zw ≠ =+ = ∑ ∑ ∑∑ 2 1 n kk kk kk kk k zw zw zw = = == ∑∑ ∑ 左边