
HCE AND 中图科萝技术大学数学 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第0章纟 绪论 ●计算方法的作用 ●计算方法的内容 ●误差 ●一些例子
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 第0章 绪论 ⚫计算方法的作用 ⚫计算方法的内容 ⚫误差 ⚫一些例子
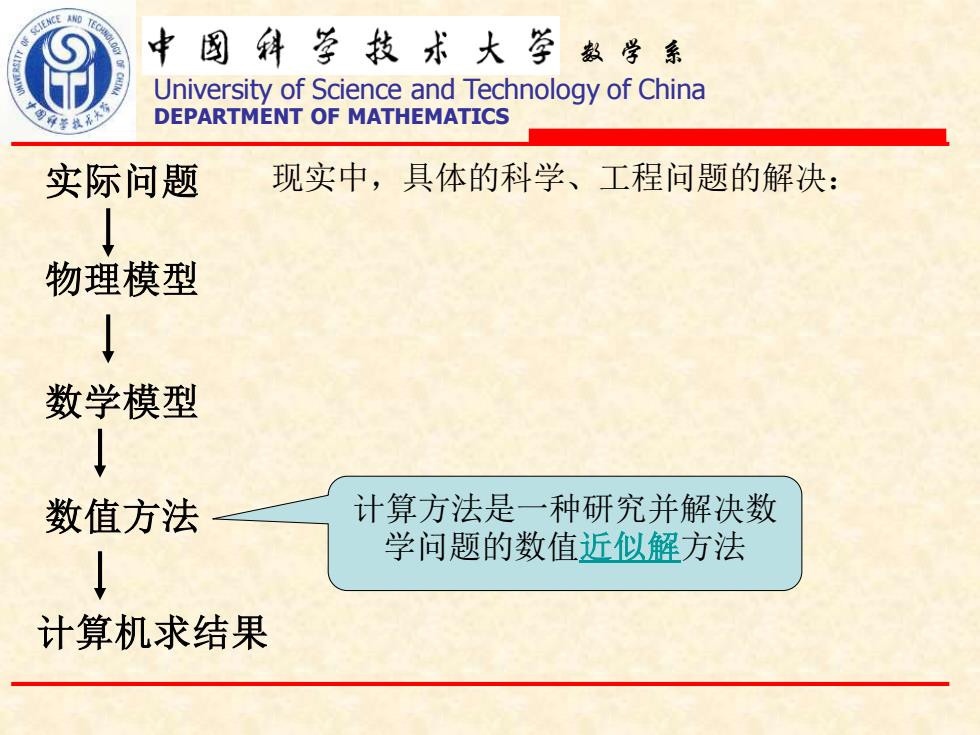
FIENCE AND 中图斜萝技术大学数学票 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 实际问题 现实中,具体的科学、工程问题的解决: ↓ 物理模型 ↓ 数学模型 ↓ 数值方法 计算方法是一种研究并解决数 学问题的数值近似解方法 ↓ 计算机求结果
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 实际问题 现实中,具体的科学、工程问题的解决: 物理模型 数学模型 数值方法 计算机求结果 计算方法是一种研究并解决数 学问题的数值近似解方法
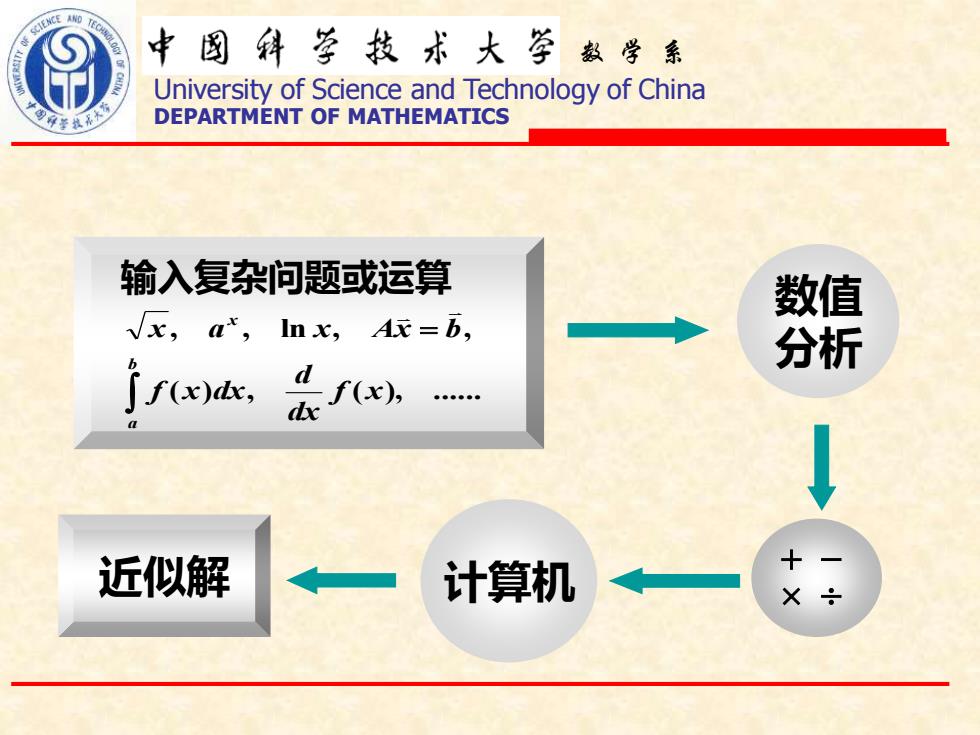
EHCE AND 中图技术大学数学 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 输入复杂问题或运算 数值 x,a*,Inx,Ax=b, 分析 ∫f(x),」 rx, 近似解 计算机
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 数值 分析 输入复杂问题或运算 ( ) , ( ), . , , ln , , f x dx d f x dx x a x Ax b b a x = + − 近似解 计算机

ENCE AND 中图科萝技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 计算方法的特性 计算方法连接了模型到结果的重要环节 ●】 理论性:数学基础 ● 实践性 随着计算机的飞速发展,数值分析方法已深入到计算 物理、计算力学、计算化学、计算生物学、计算经济学等 各个领域。本课仅限介绍最常用的数学模型的最基本的数 值分析方法
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 计算方法的特性 ⚫ 理论性:数学基础 ⚫ 实践性 计算方法连接了模型到结果的重要环节 随着计算机的飞速发展,数值分析方法已深入到计算 物理、计算力学、计算化学、计算生物学、计算经济学等 各个领域。本课仅限介绍最常用的数学模型的最基本的数 值分析方法

中图科技术大学数学 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 学习的目的、要求 ·会套用、修改、创建公式 ·编制程序完成计算 课程评分方法(Grading Policies) C☐总分(100)=平时作业(20)+上机作业(10)+期末(70)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 学习的目的、要求 ⚫会套用、修改、创建公式 ⚫编制程序完成计算 课程评分方法 (Grading Policies) 总分 (100) = 平时作业(20)+上机作业(10)+期末 (70)

ENCE AND 中图科亨技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ◆上机作业要求 1、编程可以用任何语言; (C,C++,Matlab,.Mathematica,Delphi,Fortran,.等)不允许 使用内置函数完成主要功能 2、结果输出要求小数点后至少13位 3、以E-Mail形式交: E-Mail:ustc.numerical@gmail.com ● 主题:PB05023001 内容:一次作业一个附件,并在内容中写出运行结果
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 3、以E-Mail形式交: • E-Mail: ustc.numerical@gmail.com • 主题 : PB05023001 • 内容 : 一次作业一个附件,并在内容中写出运行结果 ◆上机作业要求 1、编程可以用任何语言; (C,C++,Matlab,Mathematica,Delphi,Fortran,等)不允许 使用内置函数完成主要功能 2、结果输出要求小数点后至少13位

中图科亨技术大学教学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 内容 1、数值逼近一数学分析中的数值求解,如微分、积分、 心fa)&=F()-Fa 2、数值代数一线性代数的数值求解,如解线性方程组、 逆矩阵、特征值、特征向量 Ax=b→x,=D,/Dn=20,9.7×1020 100亿/秒,算3,000年,而Gauss消元法2660次 3、微分方程一常微分,Runge-Kutta法、积分法
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 内容 2、数值代数-线性代数的数值求解,如解线性方程组、 逆矩阵、特征值、特征向量 3、微分方程-常微分,Runge-Kutta法、积分法 1、数值逼近-数学分析中的数值求解,如微分、积分、 = − b a f (x)dx F(b) F(a) Ax = b xi = Di / D 20 n = 20,9.710 100亿/秒,算3,000年,而Gauss消元法2660次

IENCE AND 中图斜萝技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 误差 ·绝对误差 设x*为精确值,x为近似值,=x一x为误差或绝对误差 例如:f(x)=ln(x+l)作Taylor展开, rr (-l)”x+1 (n+11+)m,0<0<1 舍弃,即为误差
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 误差 ⚫ 绝对误差 设 * x 为精确值, x 为近似值, e = x − x * 为误差或绝对误差 例如: f (x) = ln( x +1) 作Taylor展开, , 0 1 ( 1)(1 ) ( 1) ( 1) 1 1 1 1 + + − + − = + + = − n n n i n i i n x x x i 舍弃,即为误差

EHCE AND 中图萝技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ·相对误差 e x"-x e, 称为相对误差 150分满考139,100分满考90,两者的绝对误差分别 为11和10,优劣如何? 前者相对误差(150一13)/150=0.073, 后者相对误差(100-90)/100=0.100
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS ⚫相对误差 * * * x x x x e er − = = 称为相对误差 150分满考139,100分满考90,两者的绝对误差分别 为11和10,优劣如何? 前者相对误差(150-139)/150=0.073, 后者相对误差(100-90)/100=0.100

ENCE AND 中图斜萝技术大学数学系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 误差来源 ●原始误差一模型误差(忽略次要因素, 如空气阻力)物理模型,数学模型 ●方法误差一截断误差(算法本身引起) ●计算误差一舍入误差(计算机表示数据 引起)
数 学 系 University of Science and Technology of China DEPARTMENT OF MATHEMATICS 误差来源 ⚫原始误差-模型误差(忽略次要因素, 如空气阻力)物理模型,数学模型 ⚫方法误差-截断误差(算法本身引起) ⚫计算误差-舍入误差(计算机表示数据 引起)