
第一章插值 2
2 第一章 插值
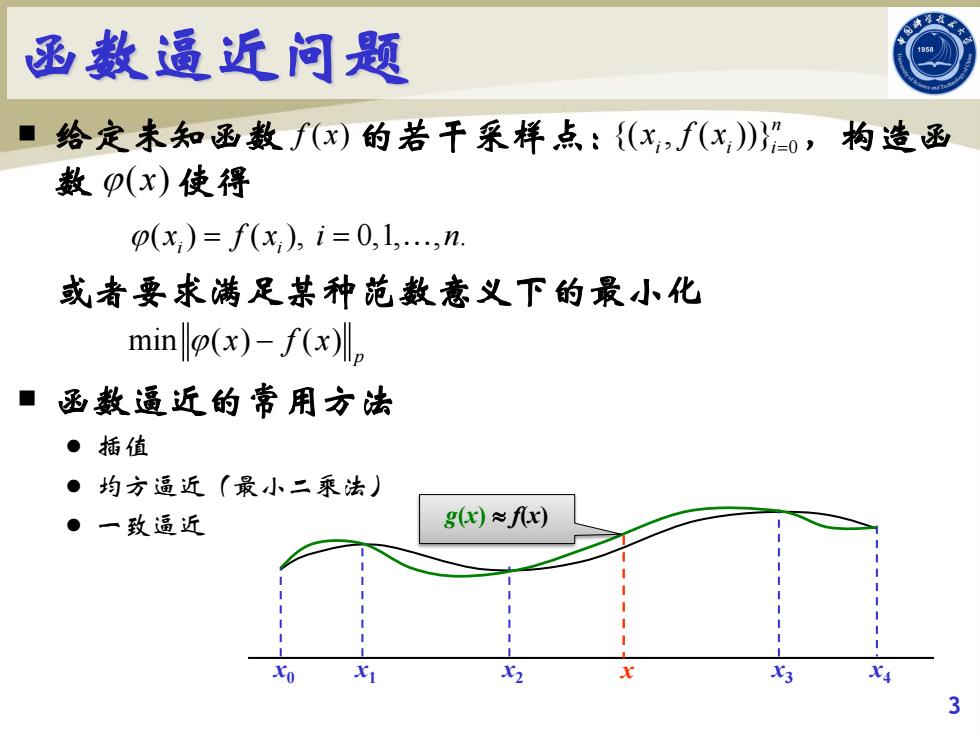
函数逼近问题 ■给定未知函数f(x)的若干采样点:{(x,f(x)}”0,构造函 数p(x)使得 p(x)=f(x),i=0,1,.,n 或者要求满足某种范数意义下的最小化 min (x)-f(x) ■函数逼近的常用方法 ●插值 ●均方逼近(最小二乘法) ●一致逼近 g(x)fx) X1 2 3
函数逼近问题 给定未知函数 的若干采样点: ,构造函 数 使得 或者要求满足某种范数意义下的最小化 函数逼近的常用方法 插值 均方逼近(最小二乘法) 一致逼近 3 f x( ) 0 {( , ( ))}n i ii x fx = ϕ( ) x ( ) ( ), 0,1, , . i i ϕ x fx i n = = min ( ) ( ) p ϕ x fx − x0 x1 x2 x x3 x4 g(x) ≈ f(x)

插值问题 1958 ■定义:f(x)为定义在区间[a,b]上的函数,xo,x1,xn为[a,b] 上+1个互不相同的点,Φ为给定的某一函数类。若Φ 上有函数p(x)满足: p(x;)=f(x),i=0,1,n 则称p(x)为f(x)关于节点o,X1,xn的插值函数 ■称X0,X,.,xn为插值节点 ■称(x,f(x)为插值型值点 ■称f(x)为被插函数
插值问题 定义: 为定义在区间 上的函数, 为 上 个互不相同的点, 为给定的某一函数类。若 上有函数 满足: 则称 为 关于节点 的插值函数 称 为插值节点 称 为插值型值点 称 为被插函数 4 f x( ) [,] a b 0 1 , , n xx x [,] a b n +1 Φ Φ ϕ( ) x ( ) ( ), 0,1, , i i ϕ x fx i n = = ϕ( ) x f x( ) 0 1 , , n xx x 0 1 , , n xx x ( , ( )) i i x fx f x( )

插值问题 ■主要问题 ●插值函数类Φ如何选取? ●插值函数p(x)是否存在? ●插值函数0(x)是否唯一? ●被插值函数f(x)与插值函数(x)之间误差如何估计? 5
插值问题 主要问题 插值函数类 如何选取? 插值函数 是否存在? 插值函数 是否唯一? 被插值函数 与插值函数 之间误差如何估计? 5 Φ ϕ( ) x ϕ( ) x f x( ) ϕ( ) x

插值问题 ■ 设p(x)=ap(x)+ap,(x)+.+a.(x),则 f(x)=(x)=aopo(x;)+ae (x)++ame (x),i=0,1.n ■ n+1个方程,m+1个未知量的线性方程组 当且仅当m=n,det(A)≠0,方程组解存在且唯一 6
插值问题 设 ,则 个方程, 个未知量的线性方程组 当且仅当 , ,方程组解存在且唯一 6 0 0 11 () () () () m m ϕϕ ϕ ϕ xa xa x a x = + ++ 0 0 11 ( ) ( ) ( ) ( ) ( ), 0,1, , i i i i mm i fx x a x a x a x i n = = + ++ = ϕϕ ϕ ϕ n +1 m +1 m n = det( ) 0 A ≠

插值问题 ■ (存在难一性定理)设{x为n+1个互不相等的节点 ,Φ=span{po,91,pn}为n+1维线性空间,则插值函数 p(x)存在雅一,当且仅当 Po(xo)2(xo) . 0n(xo) p(x)0(x) . pn(x1) ≠0 p(xn)p,(xn). pn(xn) 7
插值问题 (存在唯一性定理)设 为 个互不相等的节点 , 为 维线性空间,则插值函数 存在唯一,当且仅当 7 { } 0 n i i x = n +1 0 1 span{ , , , } Φ = ϕϕ ϕ n n +1 ϕ( ) x 00 10 0 01 11 1 0 1 () () () () () () 0 () () () n n n n nn xx x xx x xx x ϕϕ ϕ ϕϕ ϕ ϕϕ ϕ ≠
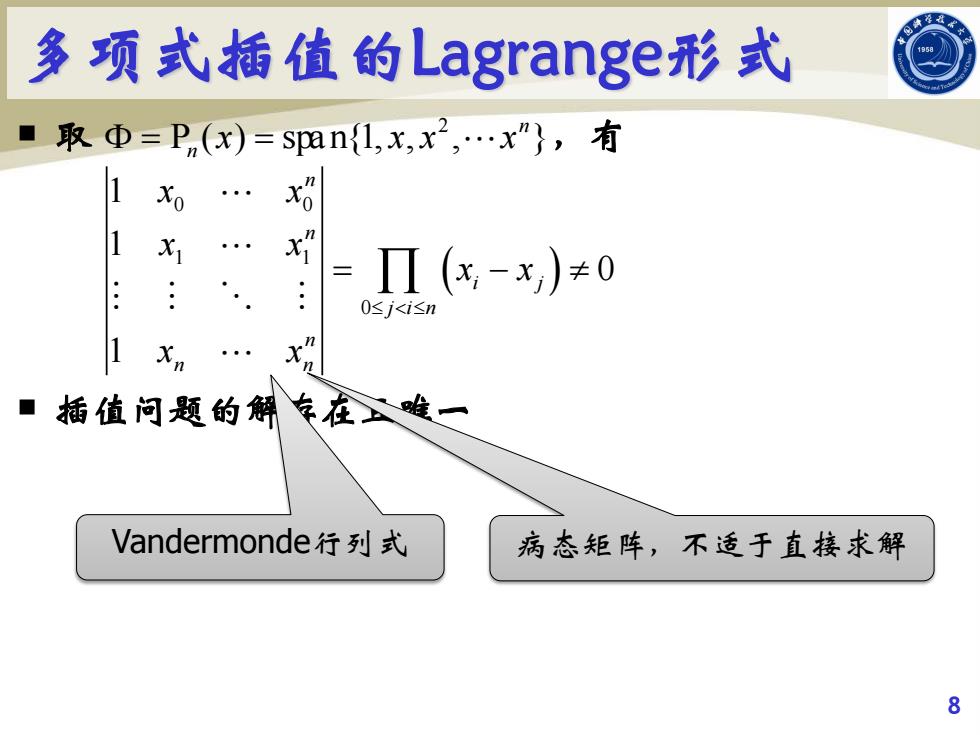
多项式插值的Lagrange:形式 1958 ■ 取Φ=Pn(x)=Sp阳n{1,x,x2,.x”},有 Xo x =Π(x-x)≠0 0sj<i≤n 7 Xn 插值问题的解年在难一 Vandermonde行列式 病态矩阵,不适于直接求解 8
多项式插值的Lagrange形式 取 ,有 插值问题的解存在且唯一 8 2 P ( ) spa n{1, , , }n n Φ= = x xx x ( ) 0 0 1 1 0 1 1 0 1 n n i j jin n n n x x x x x x x x ≤ <≤ = −≠ ∏ Vandermonde行列式 病态矩阵,不适于直接求解

多项式插值的Lagrange形式 如何选取④=Pn(x)=span{1,x,x2,.x”}的另一组基,使 得插值问题便于求解? ■Lagrange基函数{,(x)oSPn(x)满足 -8=&=0。 9
多项式插值的Lagrange形式 如何选取 的另一组基,使 得插值问题便于求解? Lagrange基函数 满足 9 2 P ( ) spa n{1, , , }n n Φ= = x xx x 0 { ( )} ( ) n ii n lx x = ⊆ Ρ 1, ( ) , , 0,1, , 0, i j ij i j l x ij n i j δ = == ∀= ≠
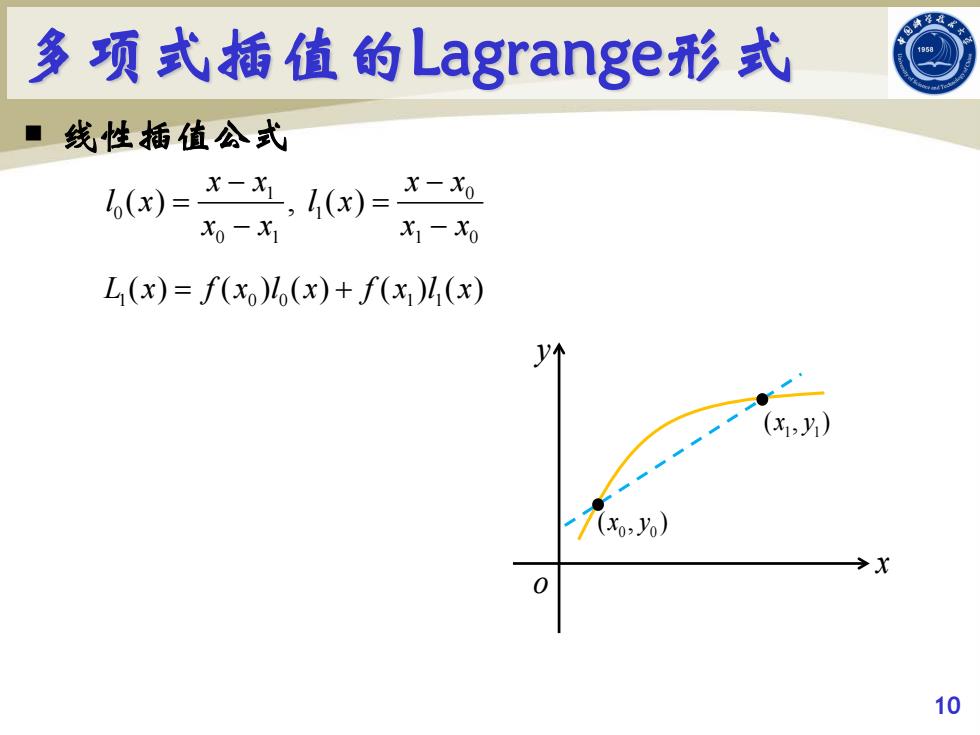
多项式插值的Lagrange:形式 958 ■线性插值公式 ,(x)=X-,14(x)=X- X0-X1 X1-X0 L(x)=f(x)(x)+f(x)(x) (x1,乃) 7(x,) →X 10
多项式插值的Lagrange形式 线性插值公式 10 o x y 0 0 (, ) x y 1 1 (, ) x y 1 0 0 1 01 10 ( ) , ( ) xx xx lx lx xx xx − − = = − − 1 0 0 1 1 Lx fxl x fxlx () ( )() ( )() = +

多项式插值的Lagrange:形式 1(误差估计)设L(x)为以(x,f(x),(x,f(x)为插值点 的插值函数,x,x1∈[a,b],x≠x.设f(x)一阶连续可导 ,f(x)在(a,b)上存在,则对任意给定的x∈[a,b],至少 存在一点5x∈(a,b),使得 ()-/()()().6c(o.) 2 11
多项式插值的Lagrange形式 (误差估计)设 为以 为插值点 的插值函数, . 设 一阶连续可导 , 在 上存在,则对任意给定的 ,至少 存在一点 ,使得 11 1 L x( ) 0 0 11 ( , ( )), ( , ( )) x fx x fx 0 1 0 1 x x ab x x , [ , ], ∈ ≠ f x( ) '' f x( ) (,) a b x ab ∈[,] (,) x ξ ∈ a b '' 1 1 0 1 ( ) ( ) ( ) ( ) ( )( ), ( , ) 2! x x f R x f x L x x x x x ab ξ =− = − − ∈ ξ