中国科学技术大学 2016-2017学年第二学期期终考试A卷 课程编号001511考试科目:计算方法B) 2017.4.23 所在院系 学号 姓名 题号 四五 六七 总分 得分 评卷人 (所有计算保留4位小数) 一·填空题(36分) 1.写出x=0.000714247的五位有效数字的近似值_x=0.00071425 17-9\ 2.已知A=0-13-10,则A=41,IA=37,p(40=2 (02116 3.计算矩阵按模最大特征值的方法是幂法,计算矩阵按模最小特征值的方法是 反幂法一,计算实对称矩阵全部特征值的方法是Jacobi_。 4.设l,(x),l(x),l,(x,l(x)是以互异的,x2,x为节点的Lagrange插值基函数则 2+2+2y 5.设f(x)为n次多项式,n>5,由数据f(0),f(0),f),f"0),f),构造插值多 项式的插值余项为 x- 6.n个节点的数值积分公式至多可以达到2n-L阶代数精度。 7.完成下列差商表 f(,) fx.x,] f[x-2,x-1,x] fx3x-2-] -7 -2 13 16
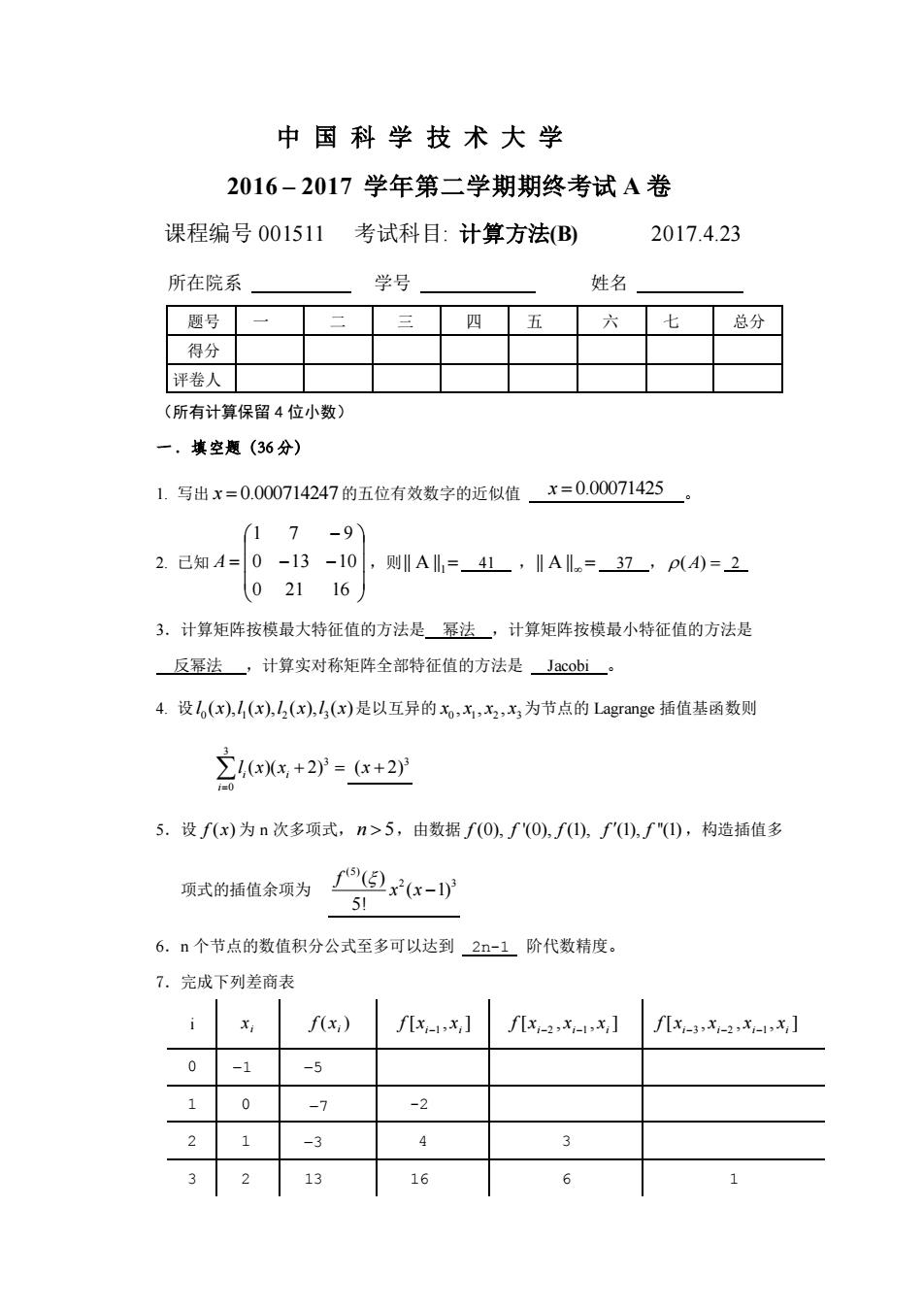
中 国 科 学 技 术 大 学 2016 – 2017 学年第二学期期终考试 A 卷 课程编号 001511 考试科目: 计算方法(B) 2017.4.23 所在院系 学号 姓名 题号 一 二 三 四 五 六 七 总分 得分 评卷人 (所有计算保留 4 位小数) 一.填空题(36 分) 1. 写出 x = 0.000714247 的五位有效数字的近似值 x = 0.00071425 。 2. 已知 − − − = 0 21 16 0 13 10 1 7 9 A ,则 || A ||1= 41 ,|| A || = 37 , ( ) A = 2 3.计算矩阵按模最大特征值的方法是 幂法 ,计算矩阵按模最小特征值的方法是 反幂法 ,计算实对称矩阵全部特征值的方法是 Jacobi 。 4. 设 0 1 2 3 l x l x l x l x ( ), ( ), ( ), ( ) 是以互异的 0 1 2 3 x x x x , , , 为节点的 Lagrange 插值基函数则 3 3 0 ( )( 2) i i i l x x = + = 3 ( 2) x + 5.设 f (x) 为 n 次多项式, n 5,由数据 f f f f f (0), '(0), (1), (1), ''(1) ,构造插值多 项式的插值余项为 (5) 2 3 ( ) ( 1) 5! f x x − 6.n 个节点的数值积分公式至多可以达到 2n-1 阶代数精度。 7.完成下列差商表 i xi f xi ( ) f x x i i [ , ] −1 f x x x i i i [ , , ] −2 −1 f x x x x i i i i [ , , , ] −3 −2 −1 0 −1 −5 1 0 −7 -2 2 1 −3 4 3 3 2 13 16 6 1

二(12分)给出下列数据 1.10 1.20 1.30 1.50 1.21 2.37 3.52 4.29 In(y,) 0.19 0.86 1.26 1.46 解:用最小二乘法求形如(x)=a“的经验公式。 (任网 lna=-2.8788,b=2.9971a=e2m=0.0562 (x)=0.0562e271 三.(12分)设函数由下表给出 1.201.251.301.501.701.751.80 f(x) 3.904.203.704.305.105.604.90 写出复化Simpson(辛普森)公式,并用复化辛普森公式计算[,fx)d 解S.U0=f@)+4f+22f)+jb) 心fd=fx+fx+fxd -09B0+4420+37+0B0+4420+37 3 095g0+4420+370=268 四.(15分)己知方程组 :期因 ()写出解方程组Jacobi达代格式:(②)写出解方程组Gauss-Seidel达代格式: (3)求出Gauss-Seidel迭代矩阵:(4)讨论Gauss-Seidel迭代收敛的充要条件
二(12 分)给出下列数据 i x 1.10 1.20 1.30 1.50 i y 1.21 2.37 3.52 4.29 ln( ) i y 0.19 0.86 1.26 1.46 解: 用最小二乘法求形如 ( ) bx y x ae = 的经验公式。 4 5.1 ln 3.77 5.1 6.59 5.069 a b = 2.8788 ln 2.8788, 2.9971, 0.0562 a b a e− = − = = = 2.9971 y x e ( ) 0.0562 = 三.(12 分)设函数由下表给出 x 1.20 1.25 1.30 1.50 1.70 1.75 1.80 f (x) 3.90 4.20 3.70 4.30 5.10 5.60 4.90 写出复化 Simpson(辛普森)公式,并用复化辛普森公式计算 1.8 1.2 f x dx ( ) 解 = + + + − = − = + 1 0 1 1 2 1 2 ( ) 4 ( ) 2 ( ) ( ) 3 ( ) m i m i n f a f x i f x i f b h S f 1.8 1.3 1.7 1.8 1.2 1.2 1.3 1.7 ( ) ( ) ( ) ( ) 0.05 0.2 [3.90 4 4.20 3.70] [3.90 4 4.20 3.70] 3 3 0.05[3.90 4 4.20 3.70] 2.68 3 f x dx f x dx f x dx f x dx = + + = + + + + + + + = 四.(15 分)已知方程组 1 1 2 2 3 3 1 1 1 1 0 0 1 x b x b x b − = (1) 写出解方程组 Jacobi 迭代格式; (2) 写出解方程组 Gauss-Seidel 迭代格式; (3) 求出 Gauss-Seidel 迭代矩阵; (4) 讨论 Gauss-Seidel 迭代收敛的充要条件

[x+= x)ax)+b (1) x=-x9 + (3分) )=-ax) +b3 x)= x)-axe)+b =-x +b, (3分) )=-ax) +b 01-a 8 (4分) (4)pS)1-a2,I1-a2k1,(5分) lak2,a≠0 五.(15分)常微分方程初值问题 =jx,八,(a≤x≤ idx y(a)=yo 用线性多步法构造p=3,q=2的显式格式的求解公式。 解按题意,积分区间为x-x小:积分节点为{xn,x-x-2} ya=y-3+∫[(x)f(x3》+4()fxn-yx》+4(x)fxnn(xnld yal=y-+laf(xn,y.)+afx。nyn)+a,fx2yn-2】(5分) 积分系数: h=- xm-3(比n-xa-xn-x-2) a-子 (9分》 计算格式:
(1) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 3 1 1 2 1 2 1 3 3 1 k k k k k k k x x x b x x b x x b + + + = − + = − + = − + (3 分) (2) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 3 1 1 1 2 1 2 1 1 3 3 1 k k k k k k k x x x b x x b x x b + + + + + = − + = − + = − + (3 分) (3) 2 0 1 0 1 0 S − = − − (4 分) (4) 2 2 ( ) |1 |, |1 | 1 S = − − , (5 分) | | 2, 0 五.(15 分)常微分方程初值问题 dy dx f x y y a y a x b = = ( , ) ( ) , ( ) 0 用线性多步法构造 p q = = 3, 2 的显式格式的求解公式。 解 按题意,积分区间为[ 3 1 , n n x x − + ];积分节点为{ 1 2 , , n n− n− x x x }。 1 3 1 3 0 1 1 1 1 1 1 [ ( ) ( , ( )) ( ) ( , ( )) ( ) ( , ( ))] n n x n n n n n n n n x y y l x f x y x l x f x y x l x f x y x dx + − + − − − − − = + + + 1 3 0 1 1 1 2 2 2 [ ( , ) ( , ) ( , )] n n n n n n n n y y h a f x y a f x y a f x y + − − − − − = + + + (5 分) 积分系数: 1 1 2 0 3 1 2 ( )( ) 8 ( )( ) 3 n n n n n n n n x x x x x a h dx h x x x x x + − − − − − − − = = − − 1 2 1 1 1 1 2 ( )( ) 4 ( )( ) 3 n n n n n n n n x x x x x a h dx h x x x x x + − − − − − − − = = − − − 1 1 2 1 2 2 1 ( )( ) 8 ( )( ) 3 n n n n n n n n x x x x x a h dx h x x x x x + − − − − − − − = = − − (9 分) 计算格式:

y=y+8fx,y)-4x以)+8/x】 (1分) y=+警2化w)-c+2gwy-】 六.(5分)推导用Doolittle分解求解线性方程组Ar=b的公式, 其中A是n阶方阵,A=LU,L是单位下三角阵,U是上三角阵 推导:计算U的第k行元素u,山4,山 a=214,=亿2.4100 2,-4,+w uy dy-g:=k.k+.m 计算L的第k列元素k+,lk2k,.,ln -2=00 =艺+e 0 a=(a-2),f=k+lk+2.,n Ax=LUx=b,Ly=b,Ux=y 解方程组LY-b: y=6-24y,i=l2,n 解方程组UX=Y: =0-三=n-小
1 3 1 1 2 2 1 3 1 1 2 2 [8 ( , ) 4 ( , ) 8 ( , )] 3 4 [2 ( , ) ( , ) 2 ( , )] 3 n n n n n n n n n n n n n n n n h y y f x y f x y f x y h y y f x y f x y f x y + − − − − − + − − − − − = + − + = + − + (1 分) 六.(5 分) 推导用 Doolittle 分解求解线性方程组 Ax = b 的公式, 其中 A 是 n 阶方阵, A LU = , L 是单位下三角阵, U 是上三角阵 推导:计算 U 的第 k 行元素 ukk uk k uk n , , , , +1 , ( ) 1 1 1 2 , 1 1 1 1 1 0 0 0 0 j n k k jj kj kr rj k k k k kr rj kr rj kj r r r u u a l u l l l l u l u u − − = = = = = = = + u a l u j k k n k r kj kj kr rj , , 1, , 1 1 = − = + − = 计算 L 的第 k 列元素 l l l k+1,k k+2,k n,k , , , aik l iru r n = rk = = 1 1 1 1 , 1 1 ( , , ,1,0, ,0) 0 0 k k kk i i i ir rk ik kk r u u l l l u l u − − = = + 1 1 ( ) , 1, 2, , k ik ik ir rk kk r l a l u u i k k n − = = − = + + Ax LUx b Ly b Ux y = = = = , , 解方程组 LY = b : 1 1 , 1,2, , i i i ij j j y b l y i n − = = − = 解方程组 UX = Y : 1 ( ) , , 1, ,1 n i i ij j ii j i x y u x u i n n = + = − = −

七.(5分)证明:求非线性方程fx)=0的根的牛顿迭代法是二阶方法。 现:如=,k=12 f(xk) 迭代方程是(x)=X-f) '(x) )("( (f'(x)2 (1分) xk1-a=(x)-(a) =a)+(x-ap'a)+- 21 -"(5)-(a) =x-a)2 21p"(65 (3分)》 (82 mlxn-a-imle=g"(a) k1x-ap leg12 (1分) 求单根牛顿迭代是二阶迭代方法
七.(5 分) 证明:求非线性方程 f x( ) 0 = 的根的牛顿迭代法是二阶方法。 证明: x x f x f x k k k k +1 = − ( ) '( ) , k = 1,2, 迭代方程是 '( ) ( ) ( ) f x f x x = x − , '( ) ( ) ' '( ) ( '( )) x f x f x f x = 2 (1 分) 1 2 ( ) ( ) ( ) ( ) ( ) '( ) ''( ) ( ) 2 ! k k k k x x x x + − = − − = + − + − ''( ) 2! ( ) 2 − = k x (3 分) ( M x x e e n k k k n k k k = − − = + → + → | | | | lim | | | | lim 1 1 ) ''( ) | | | | lim | | | | lim 2 1 2 1 = = − − + → + → k k k k k k e e x x (1 分) 求单根牛顿迭代是二阶迭代方法