
课程目标 ■掌握数值计算方法的基本原理 ·数学原理 ·基本算法 ●收敛性分析 ●误差分析 ●稳定性分析 ■ 编写数值计算方法的程序 ●利用C/C+十语言实现基本的算法 ●熟悉Matlab数值计算平台 3
3 课程目标 掌握数值计算方法的基本原理 数学原理 基本算法 收敛性分析 误差分析 稳定性分析 编写数值计算方法的程序 利用C/C++语言实现基本的算法 熟悉Matlab数值计算平台

第零章绪论 5
5 第零章 绪论

计算方法概述 实际问题 现实中,具体的科学、工程问题的解决: ↓ 物理模型 ↓ 数学模型 ↓ 数值方法 计算方法是一种研究并解决数学问题 的数值近似解方法 计算机求结果 6
实际问题 现实中,具体的科学、工程问题的解决: 物理模型 数学模型 数值方法 计算机求结果 计算方法是一种研究并解决数学问题 的数值近似解方法 计算方法概述 6
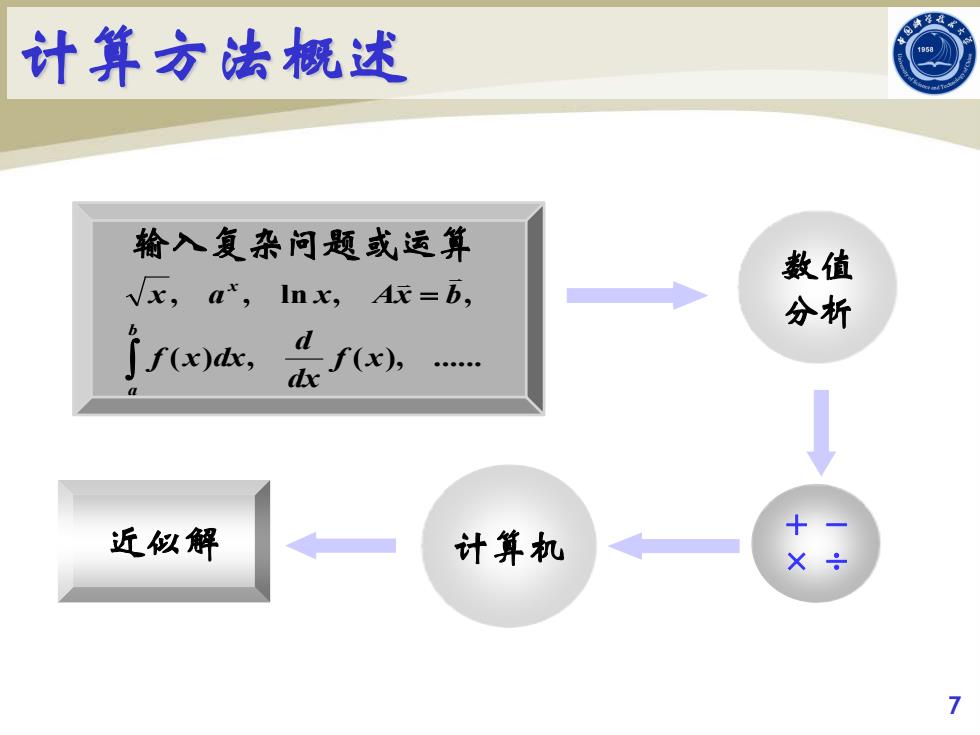
计算方法概述 输入复杂问题或运算 数值 x,a*, Inx,x=b, 分析 ∫f(x), fa, d 近似解 计算机 X
数值 分析 输入复杂问题或运算 ( ) , ( ), . , , ln , , f x dx d f x dx x a x Ax b b a x ∫ = + − 计算机 × ÷ 近似解 计算方法概述 7

计算方法概论 ■ Numerical analysis:involves the study,development, and analysis of algorithms for obtaining numerical solutions to various mathematical problems Scientific computing:solving mathematica/problems numerically on the computer is scientific computing Numerical analysis is called the mathematics of scientific computing 8
计算方法概论 Numerical analysis: involves the study, development, and analysis of algorithms for obtaining numerical solutions to various mathematical problems Scientific computing: solving mathematical problems numerically on the computer is scientific computing Numerical analysis is called the mathematics of scientific computing 8

计算方法课程的特点 1958 理论性:数学基础 实践性:算法实现 ■ 计算方法是连接模型到结果的重要环节 科学计算方法已深入到计算物理、计算力学、计算 化学、计算生物学、计算经济学等各个领城 理论方法+实验方法+科学计算方法 本课仅限介绍最常用数学模型的最基本数值求解方 法
计算方法课程的特点 理论性:数学基础 实践性:算法实现 计算方法是连接模型到结果的重要环节 科学计算方法已深入到计算物理、计算力学、计算 化学、计算生物学、计算经济学等各个领域 理论方法+实验方法+科学计算方法 本课仅限介绍最常用数学模型的最基本数值求解方 法 9

数值计算方法的基本内容 ■ 数值通近一数学分析中的数值求解,如微分、积分等 ["f(x)dx=F(b)-F(a) ■数值代数一线性代数的数值求解,如解线性方程组、 逆矩阵、特征值、特征向量 Ax=b→x,=D,/D,n=20,9.7×1020 100亿/秒,算3,000年,而Gauss萌元法2660次 ·微分方程数值解一常微分方程,积分方程,偏微分方 程等,如Runge-Kutt归法、打靶法,有限差分法,有限 元法,有限体积法,边界元法,谱方法等 10
数值计算方法的基本内容 数值逼近-数学分析中的数值求解,如微分、积分等 数值代数-线性代数的数值求解,如解线性方程组、 逆矩阵、特征值、特征向量 微分方程数值解-常微分方程,积分方程,偏微分方 程等,如Runge-Kutta法、打靶法,有限差分法,有限 元法,有限体积法,边界元法,谱方法等 ∫ = − b a f (x)dx F(b) F(a) 20 / , 20, 9.7 10 Ax b x D D n =⇒= = × i i 100亿/秒,算3,000年,而Gauss消元法2660次 10
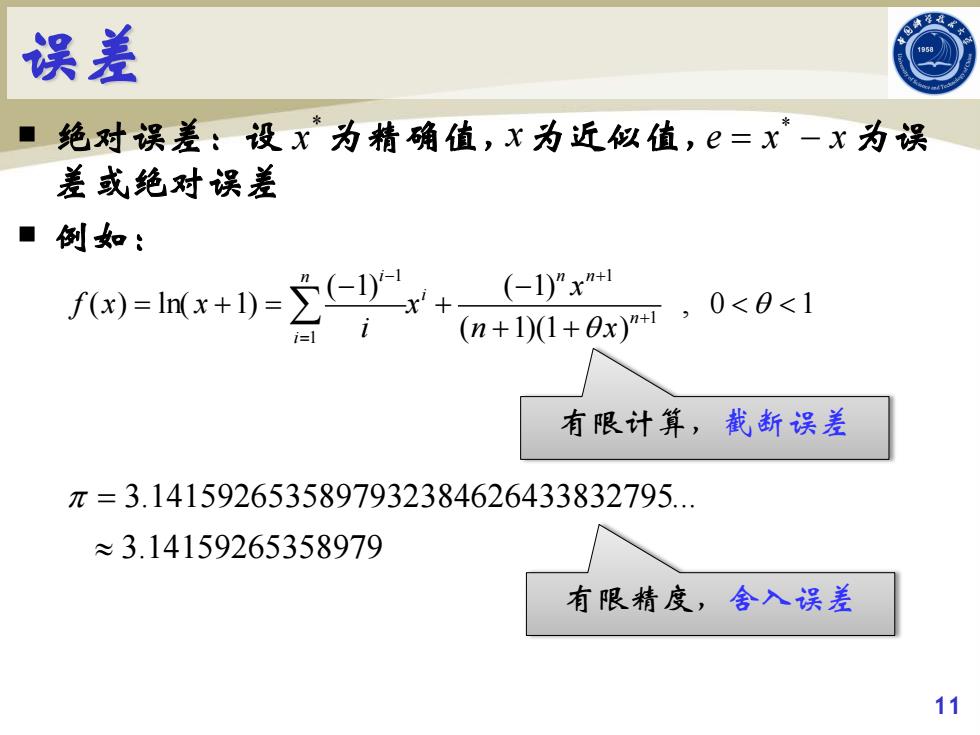
误差 ■ 绝对误差:设x为精确值,x为近似值,=X-x为误 差或绝对误差 ■例如: f)=Ix+D)-+ (-1)”x"+ i=1 i n+101+8xm,0<0<1 有限计算,截断误差 π=3.1415926535897932384626433832795. ≈3.14159265358979 有限精度,舍入误差
误差 绝对误差:设 为精确值, 为近似值, 为误 差或绝对误差 例如: * x 有限计算,截断误差 x * ex x = − 1 1 1 1 ( 1) ( 1) ( ) ln( 1) , 0 1 ( 1)(1 ) n i n n i n i x fx x x in x θ θ − + + = − − = += + < < + + ∑ 3.1415926535897932384626433832795. 3.14159265358979 π = ≈ 有限精度,舍入误差 11

误差 ■ 相对误差 e e,= 称为相对误差 X ■ 例如:150分满考139,100分满考90,两者的绝对误 差分别为11和10,优劣如何? 前者相对误差1150-139/150=0.073, 后者相对误差100-90/100=0.100 12
误差 相对误差 例如:150分满考139,100分满考90,两者的绝对误 差分别为11和10,优劣如何? * * * x x x x e er − = = 称为相对误差 前者相对误差(150-139)/150=0.073, 后者相对误差(100-90)/100=0.100 12

有效位数 ■ 当x的误差限为某一位的半个单位,则这一位到第一个 非零位的位数称为x的有效位数 ·有效位的多少直接影响到近似值的绝对误差和相对误 差 ■例: π的近似值3.141具有几位有效位数? π的近似值3.142具有几位有效位数? 13
有效位数 当 的误差限为某一位的半个单位,则这一位到第一个 非零位的位数称为 的有效位数 有效位的多少直接影响到近似值的绝对误差和相对误 差 例: π 的近似值3.141具有几位有效位数? π 的近似值3.142具有几位有效位数? x x 13